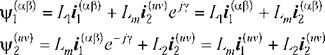ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

Потокосцепления электрической машины

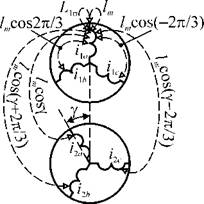
Если пренебречь насыщением магнитопровода АД, то магнитные потоки, сцепляющиеся с его обмотками, будут пропорциональны соответствующим МДС. Рассмотрим основные соотношения между этими величинами. Допустим, что ста­тор и ротор трехфазного АД симметричны, параметры обмотки ротора приведены к обмотке статора и рабочий зазор машины равномерный. Схематически эти об­мотки показаны на рисунке 1.4.

С обмоткой фазы а статора сцепляются магнитные потоки, создаваемые как ею самой, так и всеми остальными обмотками. Часть маг­нитного потока, создаваемого обмоткой сцепля­ется только с её собственными витками и назы­вается потоком рассеяния. Другая часть, помимо собственных витков охватывает также витки других обмоток и называется главным или основ­ным магнитным потоком. Индуктивность Z^, связывающая поток рассеяния обмотки с проте­кающим в ней током, называется индуктивно­стью рассеяния, а индуктивность 1т, опреде-

ляющая потокосцепление с основным потоком - взаимной индуктивностью или индуктивностью основного потока. При отсутст­вии токов в обмотках ротора можно представить потокосцепление фазы а в виде

Vlla ~ ЦоНа +tmha + ^abkb + ^асНс

где МаЬ и Мас - взаимные индуктивности статорных обмоток.

Если две обмотки статора АД имеют одинаковые параметры, то магнитный поток, создаваемый током второй обмоткой и сцепляющийся с витками первой, будет полностью идентичен потоку, создаваемому первой обмоткой и сцепляю­щимся с витками второй, при условии равенства токов и совпадения расположе­ния осей двух обмоток в пространстве. Очевидно, что при этих условиях картина магнитного поля будет одинаковой независимо от того, по какой из обмоток про­текает ток, т. е. индуктивность основного потока статорных обмоток 1т будет равна их взаимной индуктивности при условии совмещения геометрических осей.

Смещение осей обмоток в пространстве на угол 8 вызовет изменение их вза­имной индуктивности пропорциональное косинусу угла сдвига, т. е. М =MQ cos 8 = lm cos 8, где MQ=lm - взаимная индуктивность обмоток при со­вмещении их осей. С учетом выражения (п.2.2) и того, что дь = 2ті/3 и 8С = -2п/3, выражение (1.8

Индуктивность Ц = L]r_ + Lm соответствует полной индуктивности статорной обмотки, включающей ее индуктивность от потока рассеяния, индуктивность от части основного магнитного потока, созданного самой обмоткой 1т, и индук­тивность от части основного потока, созданной двумя другими обмотками статора 1т/ 2. Таким образом, полная индуктивность обмотки статора от основного

магнитного потока Lm в 3/2 раза больше ее индуктивности 1т, рассчитанной

*

при отсутствии токов в других обмотках.

В силу симметрии статора, для других обмоток можно записать аналогичные выражения - ynb=ilbLx и \)Uc = іХсІл, а затем объединить фазные проекции в обобщённый вектор потокосцепления статора при отсутствии токов ротора -

2 2 Vn = з (Vila ++УпУ) = з A [ha + hba + гіУ) = M (1-Ю)

Наличие токов в обмотках ротора приведет к появлению дополнительных со­ставляющих потокосцеплений обмоток статора. Если ось фазы а ротора смещена в пространстве на некоторый угол у (см. рис. 1.4), то взаимные индуктивности обмоток ротора и фазы а статора можно определить через соответствующие уг­лы, образуемые их осями, в виде -

Maa=Moacosr, М ba = М 0b cos(y + 2к / 3); Мса =М0с cos(y - 2тг/3)

где М0а, Моь, М0с - взаимные индуктивности обмоток при у = 0. Но взаимная индуктивность обмоток статора и ротора при нулевом смещении осей равна 1т, т. к. параметры обмоток ротора приведены к статорным и можно считать, что при совпадении их осей картина магнитного поля будет такой же, как при совпадении осей статорных обмоток. Поэтому М0а =М0Ь =М0с = М0 =1т и

маа=1т Mfce =/м cos(y + 2тс/3) і М са = lm cos(y - 2тг / 3)

Тогда полное потокосцепление обмотки фазы а статора при наличии токов ротора с учетом (п.2.2) будет

Vl2. =Maaha + Мbahb + Мcahc = Kha COSy/2 = LJ2a COSy

и по аналогии для двух других фаз:

Ч'ш = Mabha +Mbbhb + Mcbhc = Lmhb cos(y + 2тт / 3);

Vl2C = Macha +Mbchb +Mcchc = Lmhc “ 2тГ/3).

/ ҐЛ Ч **

По этим проекциям аналогично (п.2.1) можно построить вектор потокосце­пления статора с ротором

2

Vl2 = ^(Vl2a + Vl26« + Vl2c«2 ) =

3

i2a cosy + i2b cos(y + 2n/3)a + i2c cos(y -2n/3)a

и, суммируя с |УП из (1.10), получить общее потокосцепление статора, соответст­вующее режиму протекания токов в обмотках статора и ротора

Щ = Щі+Щ2= +LmheJy

В силу симметрии связей между статором и ротором аналогичное выражение можно записать для потокосцепления ротора с учетом того, что для него угол у будет отрицательным, т. к. по отношению к статору этот угол отсчитывается в от­рицательном направлении -

4*2 — 4^21 + 4*22 — ^mhe Л + ^2*2

В выражениях (1.11) и (1.12) векторы тока статора и ротора записаны в раз­личных системах координат. В первом выражении ток статора записан в непод­вижной системе координат аР, связанной со статором, а ток ротора во вращаю­щейся (смещенной на текущий угол у) системе координат uv, связанной с рото­ром, т. е. в полной записи с индексами систем координат -

Если обе части уравнения потокосцепления ротора умножить на оператор по­ворота еп, то оно будет преобразовано в систему координат статора аР и примет вид

Таким образом, форма уравнений для обобщённых векторов потокосцепле - ний не зависит от выбора системы координат и индексы системы в них можно опустить. Тогда окончательно потокосцепления статора и ротора с учетом всех токов АД можно представить в виде

|/j - Цц + Lmi2 - і|/п + У12 4^2 = Lmi + L2h = 4*21 + ^22

Из выражений (1.13) следует, что потокосцепления статора и ротора раскла­дываются на составляющие обусловленные собственным током (|/п и |/22) и то­ком другой части АД (|/12 и |/21).

Пользуясь тем, что сумма токов статора и ротора образует ток намагничива­ния АД, т. е. іх + і2 = іт, потокосцепления можно также представить через основ­ной магнитный поток \jm = Lmim = Lm (ix + i2) и потоки рассеяния статора Vi* = LA и Ротора |/2ст = L2J2 -

Асимметрия параметров АД и/или источника питания при наличии нулевого провода приводит к появлению в обмотках статора токов нулевой последователь­ности. Но для нулевой составляющей справедливо ia0 = //)0 = /с0 = /0, поэтому, под­ставляя эти значения в (1.9), получим для фазы а статора

ЧЛао = АсЛао +lmhao+ cos2тг/3• im + lmcos(-27t/3) • /1с0 = + 1т - 1т/2- 1т12) = ZqZ^

Очевидно, что аналогичные выкладки для потокосцеплений рассеяния обмо­ток фаз Ъ и с приведут к такому же результату, т. е. V|/la0 = |/ш = V|/lc0 = LXJ0. Та­ким образом, потокосцепления составляющих нулевой последовательности для всех обмоток одинаковы и определяются индуктивностью рассеяния 1^.

1.1.1. Уравнения статора и ротора в векторной форме

Уравнения Кирхгофа для фазных напряжений статора АД имею вид

dxViа. V „ , d\flb. ^ W, d\rlc *

Ща = har + —f~’ иъ = 11ЪГ1 +—JT’ и1 С = НЛ + ' .

at at dt

Перейдем к векторной форме записи, умножив второе уравнение на а, третье на а2, а затем складывая все три уравнения.

|(мі« + Щь<* + исаг) = |(*ia + hba + hca2) rx + a + Vi ъ“ + Vic«2)

В результате мы получим уравнение в векторной форме

d\fx

Щ = Щ+—Г (! -15)

dt

Аналогичные преобразования можно выполнить в системе координат uv, вращающейся синхронно с ротором, и получить

u2=hr2+^7- (1Л6)

dt

Уравнения (1.15) и (1.16) записаны в разных системах координат. Для пере­вода уравнения (1.16) в неподвижную систему координат еф умножим его на

оператор поворота ejA и представим потокосцепление ротора как = ц№)е-&

e^d[^]e-^)ldt.

Опуская после преобразований индексы системы координат, получим

. duп. dQ. dif о (л л п

Щ=Нгг 2 = hh +—7r-J^2

dt dt dt

где со = d&/dt - текущая частота вращения ротора.

Переход к неподвижной системе координат в уравнении ротора привел к раз­делению слагаемого, соответствующего ЭДС индукции, на две составляющие. Первая составляющая d\f2 / dt связана с изменением потокосцепления во времени вследствие изменения во времени токов и называется ЭДС трансформации, по аналогии с процессом ее возбуждения в соответствующей электрической машине. Вторая - со|/2 связана с изменением потокосцепления вследствие вращения ротора и называется ЭДС вращения. Разложение ЭДС индукции на составляющие яв­ляется математической операцией, связанной с преобразованием системы коор­динат при условии инвариантности мощности, но в некоторых случаях его можно истолковать, исходя из физических процессов в машине.

Уравнения (1.15) и (1.17) записаны в неподвижной системе координат и их можно объединить в общую систему для решения. Кроме того, оба уравнения можно представить в некоторой произвольной системе координат тп, вращаю­щейся с угловой частотой со(""^ • Для этого нужно проделать преобразования ана­логичные преобразованиям, выполненным при выводе выражения (1.17),

Из выражений (1.18) уравнения для любых систем координат получаются простой подстановкой соответствующей частоты вращения а/™"). В дальнейшем, если это не оговорено особо, мы будем использовать индексы систем координат, сведенные в таблицу приложения 3

Выражения (1.18) показывают, что выбором системы координат можно, ис­ключить ЭДС вращения, но только в одном из уравнений. Полагая со(“и) = 0 , мы получим уравнения в неподвижной системе координат и исключим ЭДС враще­ния в уравнении статора, а в системе координат, вращающейся синхронно с рото­ром (со^) = со), ЭДС вращения обращается в нуль в уравнении ротора.

При выборе системы координат следует учитывать, что в любой электриче­ской машине угловые частоты вращения магнитных полей статора Q, и ротора

Q2 связаны с угловой частотой вращения вала ротора Q соотношением - Q, = Q ± Q2, где положительный знак соответствует согласному направлению вращения. Но частоты вращения полей статора и ротора определяются частотами соответствующих ТОКОВ И ЧИСЛОМ пар ПОЛЮСОВ обмоток Z, Т. е. Q^COj/z^H

Q2 = со2 /z, где coj и со2 - частоты токов статора и ротора. Отсюда

coj = Q ■ zp ± со2 = со ± со2 где со = Q • zp - угловая частота вращения ротора электрической машины с одной парой полюсов.