ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ КОРОТКОЗАМКНУТОГО ДВИГАТЕЛЯ

Для аналитического расчета динамики электроприводов с замкнутой цепью частотного управления [41—44] необ­ходимо иметь выражение передаточных функций или ам­плитудно-фазовых частотных характеристик участка зам­кнутой цепи, содержащего асинхронный двигатель с пре­образователем амплитуды и частоты питающего его на­пряжения.

Под частотными характеристиками двигателя при ча­стотном управлении следует понимать зависимость ампли­туды и фазы вынужденных колебаний угловой скорости двигателя, возбуждаемых гармоническими колебаниями амплитуды и частоты напряжения, питающего статор дви­гателя. Частота напряжения при этом модулируется (по частоте же) сигналом управления.

Получить точное выражение таких передаточных функ­ций, отражающих электромагнитные переходные процессы, не представляется возможным, потому что указанная часть цепи обладает рядом существенных нелинейностей, обус­ловленных преобразованием управляющего сигнала в ча­стоту напряжения, питающего двигатель, нелинейностямикоммутации тока в вентильных преобразователях и нели­нейностью произведения токов, образующих момент двига­теля. В данном случае вопрос осложняется еще наличием двух контуров регулирования по двум взаимосвязанным входам — амплитуде и частоте напряжения.

Возможность удовлетворительной линеаризации вен­тильных преобразователей, по-видимому, можно считать доказанной. Попытки же аналитического выражения про­цессов переменной частоты далеко нельзя считать завер­шенными и даже разрешимыми. То же можно сказать про нелинейность произведения. Поэтому для электроприводов с частотным управлением особо важное значение должны получить методы расчета на аналоговых и цифровых вы­числительных машинах, которым посвящен ряд работ.

Однако использование методов моделирования и чис­ленного расчета динамических процессов не может снять актуальности аналитических методов исследования.

Без учета электромагнитных переходных процессов пе­редаточная функция асинхронного двигателя при частот­ном управлении описывается приближенно апериодическим звеном. Вопрос значительно усложняется даже при при­ближенном учете электромагнитных процессов.

Точные дифференциальные уравнения асинхронного двигателя описываются через комплексные величины из­вестными уравнениями:

(4.12)

Момент двигателя запишется уравнением

М = Re (/Т,/',) = ^-р (ЧГв/р ~ V»)’

а уравнение движения

М = Мст

В этих уравнениях потокосцепления

Для линеаризации системы уравнений, будем рассма­тривать малые отклонения системы от установившегося ре­жима. Ввиду малости отклонений будем при перемноже­нии двух функций пренебрегать всеми произведениями от­клонений высших порядков, ограничиваясь произведением отклонения на установившуюся величину. В результате после разложения комплексных уравнений на действитель­ные по ортогональным осям а и р и линеаризации получим систему

Передаточную функцию системы, представляющую со­бой зависимость угловой скорости ротора со от времени при скачкообразном изменении частоты питающего напря­жения, определить аналитически из линеаризованной схе­мы весьма трудно. Однако это можно легко сделать за счет дальнейших упрощений.

Структура постоянной k и уравнение (4.18) показыва­ют, что влияние произведения pb ДІ с увеличением ча­стоты ию уменьшается. Поэтому для повышенных частот система может быть описана только двумя последними уравнениями (4.17). Это означает, что исследуется враще­ние ротора в магнитном поле постоянной амплитуды, вра­щающемся с заданной частотой.

Исследования на моделирующей установке показали, что с умень шением частоты сою запас устойчивости системы понижается. На рис. 4.5,s, г по'хазаны временные функции для пониженной частоты а>іо = 0,2соіноч при тех же значеннях момента инерции, что и на рнс. 4.5,а, б.

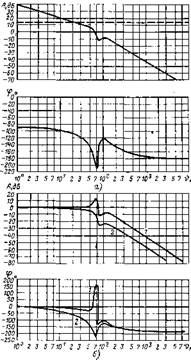
На рис. 4.6,а приведены амплітудно - и фазо-частотные характе­ристики разомкнутой системы для тех же (рис. 4.5) случаев нормаль­ного и пятикратного момента инерции. В последнем случае постоян­ные уравнения (4.59): ft,=-3,79-10-2 с 4; ^2=0,061; Т5=0,0127 с. По­стоянные схемы рис. 4.5 Гг =10,25-10”3 с; Т3— 15,2-10~3 с; <4 = 0,22 и Ыг^/ай = 102 с -1, 40,3 дБ. Пунктиром показана нулевая линия для случая пятикратного момента инерции, а = 0,25.

На рнс. 4.6,6 показаны такие же характеристики замкнутой систе­мы при нормальном (кривые 1) и пятикратном (кривые 2) моменте ниерции, также при пониженной частоте, а = 0,25. На частоте сигнала v = 65 Гц виден пик резонанса, соответствующий колебаниям на вре­менной характеристике рис. 4.5,а. При нятнкратном увеличении момен­та временная характеристика (рис. 4.5,г) становится апериодической н частотная характеристика (рнс. 4.6,6, кривая 2) ие имеет пика резо­нанса. Анализ этих кривых показывает, что для

низких частот следует пользоваться структурной схемой рис. 4.4.