ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

Основная характеристика выпрямителя

Основной характеристикой выпрямителя является внешняя харак­теристика, выражающая зависимость среднего значения выпрямленно­го напряжения от среднего значения выпрямленного тока при некото­ром постоянном значении угла включения а. Внешние характеристики обычно изображают семейством кривых U°=F(ia) при разных а= =const.

Ha рис. 3.15 показан вид внешней характеристики при a=const. Она состоит из двух частей, соответствующих прерывистым (/Ср< </кр) и непрерывным (/ср>/кр) токам.

В области прерывистых токов с уменьшением тока напряжение круто возрастает при появлении скважности тока: чем уже импульсы тока, тем большее нужно напряжение, чтобы получить требуемое сред­нее значение тока. Аналитическое выражение внешних характеристик в области прерывистых токОв получить невозможно, но можно их рас­считать.

В области непрерывного тока внешняя характеристика бестранс - форматорного выпрямителя при отсутствии сопротивления (в частно­сти, если пренебречь сопротивлением вентиля) проходит параллельно оси абсцисс (рис. 3.15, кривая 1), а ее ординаты определяются фоо - мулой (3.17).

У выпрямителя с трансформатором (а также без трансформатора, но с индуктивным сопротивлением между источником энергии и УВК) напряжение с ростом тока уменьшается из-за падения напряжения в со­противлениях трансформатора и перекрытия вентилей при коммутации (рис. 3.15, кривая 2). Теория коммутации недостаточно разработана вследствие большой сложности уравнений и дает противоречивые суждения о роли пер­вичной обмотки трансформатора. Поэтому ограничимся приближенны­ми соотношениями, пренебрегая полными сопротивлениями первичных обмоток трансформатора и омическими сопротивлениями вторичных обмоток.

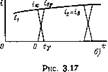
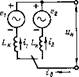
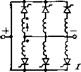
В интервале перекрытия вентилей (рис. 3.16) действительны два уравнения по контурам с вентилями:

Здесь

LK=La--LBm

— индуктивное сопротивление в одной фазе коммутирующего контура, равное сумме вторичной индуктивности рассеяния трансформатора Ьц и внешней индуктивности Z. BHI Выпрямленный ток

^2- (3.19)

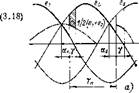
Сложив и разделив пополам уравнения (3.18), получим (рис. 3.17):

е,+е„ 1 r diB

«и= 2 2 к ~dt ' ^^

Это уравнение показывает, что в зоне перекрытия цепь коммута­ции можно записать уравнением одного эквивалентного контура, в ко­тором действующая ЭДС равна полусумме ЭДС коммутирующих фаз, а индуктивности LK соединены параллельно.

Оно образует ступенчатую функцию времени с теми же интервала­ми Тп> что и напряжение, и с ординатами iB/Tn в каждом интервале,

Важно обратить внимание на парадоксальный вывод: индуктив­ное сопротивление Хк в снижении напряжения с увеличением тока нагрузки обладает свойствами активного сопротивления, но оно не рассеивает энергии, а только уменьшает коэффициент мощности вы­прямителя.

Изложенные здесь выводы справедливы в рамках сделанных до­пущений только прн «-простой» коммутации, когда угол перекрытия вентилей y<2я/m, что и имеет место при нормальных нагрузках мо­стовых схем УВК. При этом не требовалось определять угол комму­тации y=io0tK.

Угол коммутации тем больше, чем больше электромагнитная энергия, запасенная в индуктивности контура коммутации, т. е. чем больше ток в начале коммутации. Из уравнений (3.18) можно полу­чить известную приближенную формулу для вычисления угла комму­тации

cos ос — cos (а + y) =; /в, ср-

где

Рассмотрим энергетические характеристики выпрямителя. Коэф­фициент мощности выпрямителя определяется как отношение актив­ной МОЩНОСТИ, потребляемой ИЗ сети Ііереме.-ШОГО тока Р1, к полной мощности на входе выпрямителя S:

(3.25)

Если напряжение на входе выпрямителя синусоидальной формы, то активная мощность выпрямителя Pi определяется только основ­ной гармоникой тока и для трехфазного выпрямителя

Р, = 3t/1/(i> cos ф(і),

где Uі — действующее значение фазного напряжения сети; /(и — дей­ствующее напряжение основной гармоники первичного тока; <p(i> — угол сдвига между фазным напряжением сети и основной гармони­кой первичного тока.

Полная мощность на входе выпрямителя

S—rriiUtlin,

где /|Д — полное действующее значение первичного тока.

Угол сдвига фазы сро) зависит от угла перекрытия Y, а также от намагничивающего тока трансформатора и при у>Ю_1_20о уменьша­ет коэффициент мощности X.

КПД выпрямителя может быть определен как произведение двух сомножителей

Т)=Т| т Т| в 5

где т|т — КПД трансформатора; т)в — КПД реального УВК,

Рг

Чв - рг + рв •

В последней формуле: Р2 — выпрямленная мощность, отдаваемая нагрузке; Рв —• суммарная мощность пОгерь в вентилях.

В пренебрежении пульсацией выпрямленного тока

P2=UBlB.

Габариты и мощность выпрямительного трансформатора опреде­ляются полными мощностями его первичной и вторичной цепей.

Коэффициент мощности выпрямителя согласно (3.25) опреде­ляется произведением

Л=ц cos фь

Здесь cos фі — коэффициент сдвига фазы первичного тока; [г= =Лпд/Лд — коэффициент искажения синусоидальности (отношение действующего значения основной гармоники первнчного тока /о)Д к полному действующему значению первичного тока Лд).

В пренебрежении пульсацией выпрямленного тока коэффициент искажения равен коэффициенту выпрямления (3.5):

т я V-=km = — sin—.