ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Обобщённая электрическая машина
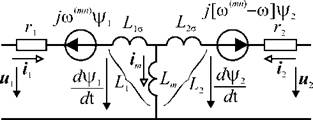
Уравнения (1.18) можно графически представить электрической схемой, показанной на рис. 1.5. Она отличается от схемы замещения трансформатора наличием источников ЭДС вращения в цепях статора и ротора.
|
|
|
U2n=r2hn + |
|
dt |
|
+ [coirawj-co]y |
|
2m |
|
Рис. 1.5. Схема замещения обобщённой электрической машины. |
|
(1.19) |
|
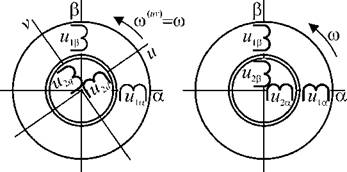
Проекции векторов на оси координат можно рассматривать как величины, соответствующие обмоткам, расположенным на взаимно-перпендикулярных осях. В этом случае уравнения (1.19) будут соответствовать двухфазной электрической машине с одной парой полюсов, модель которой показана на рис. 1.6. Такая электрическая машина называется обобщённой (ОЭМ). Если уравнения статора и ротора представлены в собственных системах координат, то модель ОЭМ будет соответствовать рис. 1.6. а). В случае записи обоих уравнений в неподвижной системе координат статора (еф) моделью ОЭМ будет трансформатор с двумя независимыми обмотками на статоре и двумя обмотками на роторе (рис. 1.6. б), в которых эффект движения ротора будет представлен посредством ЭДС вращения. Уравнения для фазных величин в этом случае мы получим из (1.19) полагая со^ = О dVla. ,^1Р. |
|
rlha+- |
|
щ+- |
|
U |
|
и |
|
1а |
|
ip |
|
dt ’ dy 2а |
|
dt ’ d\f2 р |
|
Г212а + |
|
+ |
|
r2h$ + |
|
соу2с |
|
U |
|
2а |
|
dt ‘dt При выводе уравнений (1.18) использовался ряд допущений, поэтому все они должны быть распространены и на модель обобщённой машины, т. е.: 1. машина симметрична и имеет равномерный воздушный зазор; 2. магнитопровод машины ненасыщен; 3. МДС обмоток имеет синусоидальное распределение по рабочему зазору. Модель ОЭМ универсальна и при принятии определенных условий, из нее можно получить все типы электрических машин как частные случаи. Например, при питании обмоток статора от двух источников переменного синусоидального тока, смещенных по фазе на 90° |
щающееся магнитное поле. Если одну из обмоток ротора подключить к источнику постоянного тока, то мы получим модель синхронной машины. Если обе обмотки ротора замкнуть накоротко, то образуется модель асинхронной короткозамкнутой машины. Наконец, если одну из обмоток статора подключить к источнику постоянного тока, а обмотки ротора подключить к двум источникам переменного синусоидального тока с частотой, равной частоте вращения ротора, и фазовым смещением в 90° , таким образом, чтобы поле ротора вращалось в направлении противоположном направлению вращения его вала, то мы получим модель машины постоянного тока. В этой модели поле ротора формируется источниками питания переменного тока с управляемой частотой, роль которых в реальной машине играет источник постоянного тока и коллектор, выполняющий функцию механического инвертора.
|
|
|
а) |
|
Рис. 1.6. Пространственная модель обобщенной электрической машины в различных системах координат. |
|
б) |
Основной конечной величиной характеризующей электромеханическое преобразование является электромагнитный момент на валу. Он образуется в результате взаимодействия магнитного поля и тока, протекающего в обмотках статора или ротора, и может быть представлен в виде векторного произведения
m = ^zpC{axb), *
где - zp число пар полюсов машины, а С - коэффициент, зависящий от выбора векторов а и b (см. таблицу 1.1).
|
Коэффициенты С уравнения электромагнитного момента Таблица 1.1
|
|
В таблице 1.1: kx = Lm! L{, к2 = Lm /L2‘, CJ = 1 — kxk2 - соответственно, коэффициенты электромагнитной связи статора и ротора и коэффициент рассеяния; * - означает, что электромагнитный момент не может быть выражен через произведение основного потока и потоков статора и ротора. |
В выражениях для момента физический смысл имеет только модуль вектора т и его можно определить через проекции векторов сомножителей как
Множитель 3 в уравнении момента в общем случае равен числу фаз статора /иьа делитель 2 = [2 ■ sjl соответствует преобразованию модулей векторов сомножителей в действующие значения.
ґ * л ab
|
m = —zC -1т 1 1 2 р |
|
= 2ZPC(ambn-anbm)- |
v у
Например, в произвольной системе координат электромагнитный момент определяется через потокосцепление и ток ротора в виде
3 3 3
|
т |
= ~^2р(Ът + Mn)X(l2m +Jhn) = ~llZp(V2mhn-V2nhm)=^Zp(V2nhm-V2mhn)