ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

Информационная функция УВК

Информационная функция УВК в замкнутых системах автоматического управления по существу сводится к уси­лению напряжения, так как мощность определяется обыч­но не управлением привода, а нагрузкой приводимой ма­шины.

Напряжение на выходе УВК содержит непрерывную полезную составляющую выпрямленного напряжения иъ и составляющую искажений квантованием Д:

ив=и%--А,

Полезная составляющая представляет собой модули­рованное сигналом управления иу среднее значение вы­прямленного напряжения

ыРв ““ Ку^у,

а искажения квантования — модулированные пульсации. Они являются случайной функцией времени — шумом квантования, так как их фаза неизвестна.

Коэффициент усиления для неискаженного воспроизве­дения сигнала должен иметь постоянное, в пределах до «насыщения» значение. Обобщим на режим управления определение полезной составляющей в стационарном ре­жиме, основанное на интегральной, среднеарифметической оценке пульсаций:

а = 7^ j (uB—Kyuy)dt,

О

где tn = ^Тп; Wn— продолжительность п-го интервала кван-

П

тования.

Таким образом,

тп

2л п П О п

где t — время, отсчитываемое от начала каждого интер­вала.

Усиление будет неискаженным, если Д = 0 при всех п. Для этого достаточно, чтобы на каждом интервале

Тп

An==77 j (и*п- Kyn“n)dt-=0, (3.4)

о

а коэффициент усиления не зависел от номера интервала:

/Cyn=/Cy=COnst,

откуда

т т

П П

j uBdt = Ky j Uydt. о о

Следовательно, для неискаженного усиления сигнг управления выпрямителем достаточно, чтобы в кажд интервале квантования (непрерывности) среднее значен выпрямленного напряжения равнялось среднему значен сигнала управления, умноженному на коэффициент уси„ ния, а коэффициент усиления имел постоянное значеі во всех интервалах.

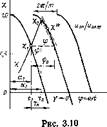
В случае вертикального управления «арккосинусны СИФУ возникают нелинейные динамические искажен зависящие от сигнала управления и его производной, причина заключается в том, что продолжительность иьт вала квантования (и их частота, соответственно) п управлении не остается постоянной, а уменьшается с ус* рением и возрастает с замедлением сигнала управлен. (рис. 3.10).

Отсюда возникает динамическая погрешность Ап=Е (km п kmo) Хсри, или в относительных единицах

&п=— An / ^Хср n—^fem п &т0,

которая однозначно определя­ется длительностью интерва­

ла ij3n, а последний, в свою очередь, зависит от сигнала

управления и его производной.

Эти зависимости можно

Облучить с хорошим приближением из двух уравнений (см, рис. 3.10):

1 , ,

/л /л, л X *Y

(to - ф) vі - у:

где tg q>=cos у, a sinv=x*; Xi<%*

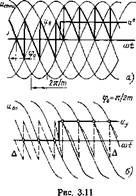
Длительность интервала i|) ограничена пределами 0^ <і])<2я//п + я. Ускорение сигнала не ограничено, а замед­ление ограничено. Однако удобно считать, что УВК отра­батывает скачок сигнала обоих знаков без инерции, но

с изменением спектра шума квантования (рис. 3.11). В действительности скачок сигнала управления не может вызвать реакции УВК внутри интервала непрерывности, и это явление иногда рассматривается как чистое запазды­вание на время т, которое является случайной величиной 0<т-<7’и. Отнесение ее к шумам упрощает описание про­цесса.

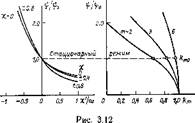
Попытки заменить статический коэффициент усиления /Су динамическим звеном, чтобы уменьшить в расчетах ошибку Д, видимо, не актуальны, так как возможность удовлетворительной аппроксимации нелинейной, трансцен­дентной функции более чем сомнительна. С другой стороны, динамическая ошибка УВК в ряде случаев пренебрежимо мала. На рис. 3.12 показана зависимость функции km от интервала гр, а г|) — от производной относительного сигнала х ПРИ разных его значениях. Погрешность 8=Кт—Кро ограничена потому, что ограничен интервал гр. Она умень­шается с увеличением числа фаз т и мала при т=6.

Благодаря введению постоянного коэффициента усиле­ния и шумов квантования осуществляется переход от ди­скретного описания процессов УВК к непрерывному со всеми преимуществами последнего. Невязка между не­прерывным представлением и дискретной природой про­цессов в УВК уходит в область шумов. Шумы же также аппроксимируются суммой непрерывных гармоник, моду­лированных сигналом управления.