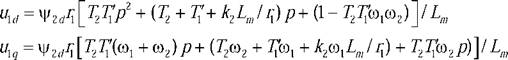ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Информационная часть систем трансвекторного управления
При построении систем трансвекторного управления в той или форме используются математические модели АД, позволяющие создать независимые каналы управления продольной и поперечной составляющими тока статора.
Рассмотрим это вначале на примере токового управления, т. е. такой системы управления, которая формирует фазные токи статора. Для упрощения выражений ограничимся двухфазным представлением машины, т. к. отличие его от трехфазного заключается в несущественном для нашей задачи преобразовании числа фаз умножением на постоянные коэффициенты.
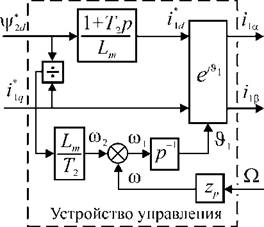
Из выражения (2.16) для электромагнитного момента АД управляемого током статора следует, что регулирование может осуществляться двумя сигналами: потокосцеплением i|j2d, а также частотой ротора со2 или поперечной составляющей тока статора iXq. Остановимся вначале на системе с управляющими сигналами i|J2d и со2. Внутри АД (рис. 2.19) продольная ixd и поперечная iXq составляющие формируются из синусоидальных фазных токов iXa и ijp переходом к синхронной системе координат с помощью ротатора е7'и'. Поэтому, если в устройстве управления (УУ) осуществить обратное преобразование e'!i' и реализовать уравнения (2.14), связывающие составляющие тока ild и i](/ с потокосцеплением
|
Рис. 2.20 Устройство управления с поперечной составляющей тока в качестве входного сигнала |
координат (РК), т. к. он формирует сигналы, соответствующе независимым (развязанным, разделённым) проекциям вектора тока статора.
Если в качестве входных сигналов устройства управления использовать цj2d и ilq,
то структура УУ будет иметь вид рис. 2.20 По структурной схеме рис. 2.19 нетрудно проследить, что передаточная функция блоков, включенных между точками схемы соответствующим сигналам потокосцепления и частоты ротора равна единице
(М72d = Чh<i' ю2 = ^г)’ т-е - устройство управления по существу является частью модели двигателя с обратными передаточными функциями. Поэтому при отсутствии погрешностей в определении параметров АД структура рис. 2.19 полностью идентична структуре рис. 2.21 а. Передаточная функция устройства рис. 2.21 а) по моменту соответствует безинерционному звену, а по скорости вращения - интегрирующему
т{р) _3zpVL _ h. O(jo) _ 1
|
ю2(р) |
|
2 г, |
ю2Ы Ттр
|
где Т = |
= J/h - механическая постоянная времени, ah - жесткость ме
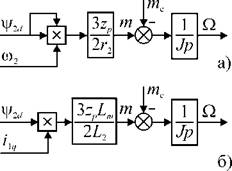
ханической характеристики (2.17). При использовании в качестве входного сигнала поперечной составляющей тока эквивалентная схема системы трансвекторного управления имеет вид рис. 2.21 б).
|
Рис. 2.21. Эквивалентные структурные схемы АД при трансвекторном управлении различными входными сигналами. |
В статическом режиме АД в этой
системе имеет абсолютно мягкую механическую характеристику и для получения характеристик, соответствующих выражениям (2.17)-(2.18), требуется обратная связь по скорости вращения.
Следует отметить, что УУ рис. 2.19 может выполнять свои функции только при условии, что параметры АД, входящие в передаточные функции его звеньев соответствуют истинным значениям, в противном случае возникает рассогласование систем координат двигателя и устройства управления, приводящее к потере работоспособности привода. Это обстоятельство создает значительные трудности при реализации систем векторного управления на практике, т. к. параметры АД изменяются в
процессе работы. В особенности это относится к значениям активных сопротивлений.
Система управления на рис. 2.19 предполагает формирование токов в обмотках статора, т. е. питание двигателя от источника электрической энергии, обладающего свойствами источника тока. Однако на практике возможно использование источников ЭДС или напряжения. В этом случае принцип построения системы управления остается прежним, но в ней используются уравнения модели АД, управляемого напряжением статора. Собственно, это касается только блока развязки координат. При выборе для УУ тех же входных сигналов (v|f2d и со2),
преобразуем уравнения проекций напряжения статора (2.21) к виду
|
|
Очевидно, что реализация этих функций затруднительна и на практике ошибки выполнения математических операций и отклонения параметров АД от значений включенных в передаточные функции звеньев приведут к полной неработоспособности устройства. Облегчить задачу можно, если учесть, что ротор АД обладает очень большой электромагнитной постоянной времени и его потокосцепление может изменяться только относительно медленно, т. е. d\f2d/ dt~ 0 . Тогда уравнения (2.22) преобразуются к виду
= V2^(!- Т2Т^2)Ит: ulq = ^2drl[Tl(0l + T2{l+T;p)m2]/Lm
|
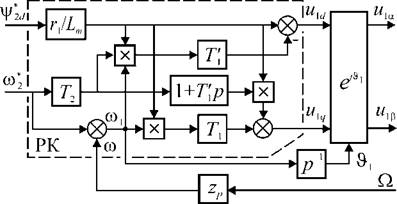
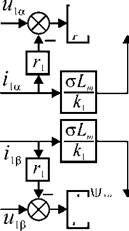
Рис. 2.22. Структурная схема устройства управления напряжением |
Структурная схема устройства управления, в котором реализованы эти функции приведена на рис.
2.22. Оно существенно сложнее, чем устройство управления для системы с формированием тока статора АД (см. рис. 2.19). Кроме того, в нем использованы приближенные выражения, вносящие ошибку в динамических режимах. Поэтому системы управления с формированием напряжения статора применяются редко.
Выбор частоты ротора со2 в качестве входного сигнала УУ не является обязательным. Часто трансвекторные системы строятся с использованием поперечной составляющей тока статора ilq вместо со2. Функциональная схема одной из
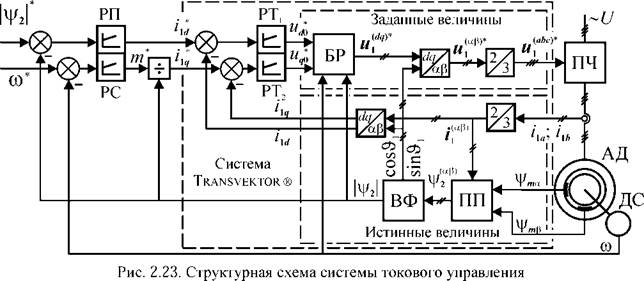
первых эффективных реализаций такого устройства, применяемых в различных вариантах до настоящего времени, показана на рис. 2.23.
Это справедливо только для синхронной системы координат.
|
|
Здесь трехфазный АД питается от преобразователя частоты, обладающего свойствами источника напряжения. В рабочем зазоре двигателя размещены датчики Холла, с помощью которых измеряются ортогональные составляющие основного магнитного потока и ц/^. В двух фазах статора установлены также
датчики тока, сигналы которых ila, ilb затем преобразуются (3/2) в ортогональные проекции вектора тока статора в неподвижной системе координат.
С помощью полученных проекций векторов тока статора и потокосцепления в зазоре в блоке преобразования потока (ПП) вычисляется потокосцепление ротора в неподвижной системе координат в соответствии с выражением
ч4“р) =v«p>y—^“wAo =>ч'2« = ч'дП^“-4аАо:ч'гр = ч'дР^“-4рАа-
т т т
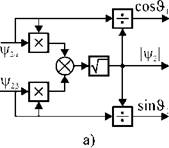
Затем с помощью так называемого вектор-фильтра (ВФ) (рис. 2.24 а) вычисляются модуль потокосцепления ротора ||/21 = +^2р и тригонометрические
функции, определяющие текущее положение синхронной системы координат в пространстве - cosS1 = vj/2a/|j/21; sinS1 = vj/2p/|ц/2|. Таким образом, с помощью
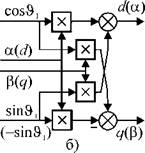
описанных блоков формируются сигналы, обеспечивающие переход от неподвижной системы координат к синхронной и наоборот. Последним этапом преобразования величин, полученных измерением (истинных величин), является вычисление продольной и поперечной составляющих тока статора ild и iXq с помощью ротатора (ар/dq). Структура ротатора показана на рис. 2.24 б). Изменение знака синусной функции приводит к изменению направления вращения, т. е. преобразование а(3/dq изменяется на противоположное dqlар.
Система управления рис. 2.23 имеет два независимых внешних контура обратных связей: по скорости вращения и по потокосцеплению ротора и два подчиненных контура по составляющим тока статора, образующим вместе отрицательную связь по вектору тока. Информация о частоте вращения поступает с
выхода датчика скорости (ДС).
|
|
|
|
|
Рис. 2.24. Структурные схемы вектор-фильтра (а) и ротатора (б). |
После вычитания из сигнала задания со*, полученный сигнал ошибки подается на регулятор скорости (PC), на выходе которого формируется сигнал задания момента т, а затем, после деления на величину модуля |ц/2|, сигнал задания поперечной составляющей тока статора ilq. Стабилизация потокосцепления осуществляется с помощью регулятора потока (РП), формирующего сигнал задания продольной составляющей тока статора ild. Преобразователь частоты (ПЧ), питающий статор АД, управляется сигналами задания фазных напряжений u[abc)*, но, будучи охваченным отрицательной обратной
связью по току статора, работает в режиме источника тока.
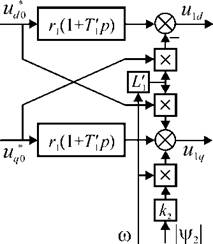
Блок развязки координат (БР) можно построить на основе уравнений модели АД, управляемого напряжением (2.22). В них можно положить d\i2d/dt& 0 и
C0j ^со. Тогда, с учетом того, что цJ2d = |v|/2|; udQ =ild uqQ =ilq, уравнения БР будут иметь ВИД
qrf = *wi(i+А'
% = VI (1+ Щ + +4^2 1*2
представленный в виде структурной схемы на рис. 2.24.
|
Рис. 2.25. Структурная схема блока развязки координат. |
Полученный на выходе БР вектор заданного напряжения статора u[dq)*, преобразуется далее ротатором dqt а(3 в неподвижную систему координат ц(сф) а затем разделяется на фазные проекции u[abc) которые являются сигналами управления для ПЧ.
В системе трансвекторного управления рис. 2.23 в качестве входных сигналов использовались фазные токи и ЭДС датчиков Холла, измеряющих магнитный поток в зазоре АД. При использовании достаточно мощного процессора для обработки информации можно отказаться от датчиков магнитного потока и вычислять потокосцепление ротора, пользуясь уравнениями статора и потокос - цеплений в неподвижной системе координат
= ц - VI>г = (V|Zj - ipL /k^lкг (2.23)
dt
kx = LJД; к2 = LmlL2 g = 1 - кхк2 - соответственно коэффициенты электромагнитной связи статора и ротора и коэффициент рассеяния. В результате потокосцепление ротора будет определяться по мгновенным значениям напряжения и тока статора так, как это показано на структурной схеме рис. 2.26.
|
і пі |
|
1 Ч"1а ^ |
|
-р — |
|
Рис. 2.26. Структурная схема устройства идентификации потокосцепления ротора. |
|
|
|
V2c |
|
ML |
В системах трансвекторного управления предназначенных для широкого применения обычно не используют датчиков скорости, т. к. её также можно вычислить по легко наблюдаемым фазным напряжениям и токам статора
И далее, разделяя проекции векторов -
|
|
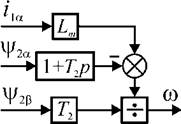
Ч>га(1+ТгР)+Ц>2^Тг=а1ш
Уг^1 + ТгР)-Уго&Тг=к$1т Для вычисления со можно использовать любое из двух уравнений, но в первом из них ток статора представлен ос - проекцией, т. е. истинным значением тока в фазе a. Поэтому для уменьшения погрешно-
^ой^а^датафикадии3 сти лУчше этой Иели выбрать его - частоты вращения АД. ш = ^ (1 + Тг р)/у г? Т2
Таким образом, используя проекции вектора тока статора и полученные с помощью выражений (2.23) проекции потокосцепления ротора, можно определить угловую частоту вращения ротора АД.
В устройствах управления всех рассмотренных выше трансвекторных систем обработка информации производится в ортогональных системах координат. Однако большинство АД имеют трехфазные обмотки статора и сигналы, формирующие токи или напряжения в них, должны быть представлены в трехфазных координатах. Соответственно и измеряемые значения фазных токов и/или напряжений перед обработкой информации должны быть преобразованы в ортогональную систему координат. Эти преобразования представляют собой элементарные арифметические операции никоим образом не влияющие на процессы в системе. Поэтому во многих задачах анализа они могут быть опущены, но в реальных устройствах преобразователи числа фаз в программном или аппаратном виде присутствуют. Их также нужно включать в модель АД, если исследуются
процессы в системе совместно с преобразователем частоты или усилителем мощности.