ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Электромагнитный момент
Определим электромагнитный момент АД, воспользовавшись векторным представлением токов намагничивания и ротора
|
|
|
где тх - число фаз статора; zp - число пар полюсов; i2 и im - пространственные векто - jx ры токов ротора и намагничивания; /2тах и |
|
|
|
+J |
|
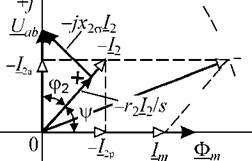
Рис. 1.18. Векторная диаграмма АД при токовом управлении |
|
2 max |
|
Ля max _ их модули или амплитуд, a sinv)/ - / угол между векторами (рис. 1.18). Но |/ + ф2 = 7г/2 sinvj/ = С0Бф2. Учитывая это |
|
равенство и переходя к действующим значениям, получим |
|
|
где /2а - активная составляющая тока ротора.
Хо
Нетрудно заметить, что выражение (1.38) представляет собой формулу Клос - са, но в отличие от режима питания источником ЭДС, в ней отсутствуют элементы asK = isK /r2. Это вполне объяснимо, т. к. питание от источника тока исключает влияние на процессы в АД падения напряжения в цепи статора (rx + yxlCT) и в этом смысле эквивалентно условию гх = х1а = 0. Как следствие этого, критические моменты при токовом питании в двигательном и генераторном режимах одинаковы (сплошная линия на рис. 1.19) и вся механическая характеристика симметрична относительно точки холостого хода. Сравнивая критические моменты в двигательном режиме при двух видах питания и полагая, что ток статора равен номи
На самом деле это отношение будет большим, т. к. номинальный момент здесь рассчитывается по значению тока ротора при условии приближенного равенства /2 « /1ном, в то время как /2 < /1ном. Способность АД развивать больший
момент при питании от источника тока широко используется для разгона гиродвигателей.
Проанализируем теперь влияние частоты источника питания на механическую характеристику АД. В соответствии с (1.38) эта характеристика полностью определяется двумя параметрами - критическим моментом Мк и скольжением sK.
Величина критического момента не зависит от частоты, а критическое скольжение можно представить в виде
|
|
х2 0^2
|
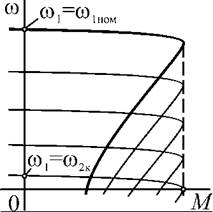
Рис. 1.20. Механические характеристики АД при частотнотоковом управлении |
Но скольжение по определению является отношением частоты ротора к частоте статора, т. е. sK = о2к /coj. Следовательно, частота ротора соответствующая критическому скольжению равна Ш2к —1/7^ = const = GDj - сок, поэтому при ИЗМЄНЄ - нии частоты питания coj частота вращения соответствующая критическому скольжению сок будет изменяться так, чтобы разность этих частот оставалась постоянной. Таким образом, с изменением частоты механические характеристики будут просто смещаться параллельно естественной характеристике (рис. 1.20).
Предельный случай снижения частоты пита-
ния с сохранением перегрузочной способности двигателя показан на рис. 1.20. Он соответствует равенству пускового и критического моментов (Мп = Мк) или условию се^ = се>2к, т. к. при дальнейшем смещении характеристики вниз ее рабочий
участок и запас устойчивости уменьшаются, будучи ограничены пусковым моментом. Тогда диапазон регулирования скорости вращения составит
|
|
и будет существенно больше, чем при питании от источника ЭДС. В реальной машине это значение несколько меньше, т. к. на него влияют насыщение магнито - провода, вызывающее уменьшение Lm и, следовательно, L2, а также нагрев обмотки ротора, приводящий к увеличению г2.