ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

ЧАСТОТНЫЙ ПУСК, РЕВЕРС И ТОРМОЖЕНИЕ

При исследовании переходных процессов в электропри­водах с асинхронными двигателями в первом приближе­нии пренебрегают электромагнитными переходными про­цессами и ограничиваются электромеханическими, считая, что время установления электромагнитных процессов пре­небрежимо мало по сравнению с механическими процесса­ми изменения угловой скорости и момента, которые замед­лены. моментами инерции системы привод'—рабочая ма­шина^

Аналитическое исследование и тем более расчет элек­тромагнитных процессов встречают большие трудности изза существенной нелинейности системы дифференциальных уравнений, описывающих двигатель, обусловленной тем, что момент выражается через произведение токов (см. § 4.3). Кроме того, не всегда можно пренебрегать насы­щением стали машины. Поэтому представляется целесооб­разным во многих случаях аналитическое исследование переходных процессов ограничивать электромеханически­ми процессами, а электромагнитные процессы исследовать с помощью аналогового и цифрового моделирования. Ме­тодика последнего разработана в настоящее время доволь­но полно и представляет самостоятельный вопрос. Поэто­му рассмотрим сначала механические переходные процес­сы частотного управления, которые можно основывать на характеристиках электропривода, полученных в установив­шемся режиме и рассмотренных в гл. 1.

При таком подходе в ряде случаев электромагнитные процессы можно исследовать в стационарном режиме, счи­тая скорость постоянной, что существенно облегчает за­дачу.

Рассмотрим сначала качественную сторону переходных процессов пуска, реверса и торможения короткозамкнуто­го асинхронного двигателя при управлении плавным изме­нением частоты в номинальном режиме f//f=const. •

С этой целью воспользуемся методом фазовых траекто­рий, но не в обычно применяемой системе координат (про­изводная в зависимости от самой координаты), а в коор­динатах механических характеристик двигателя скорость— момент (см. рис. 2.8,6).

В применении к исследованию задач динамики электро­привода такая система координат более удобна. Она уста­навливает соотношение между параметрами двигателя и его статической и динамической нагрузкой, описываемой при переходных процессах траекторией, изображающей точки ш, М с временем в качестве параметра.

Все дальнейшие рассуждения и выводы мржно распро­странить и на управление группой одинаковых двигателей при условии, что изменение их скорости в процессе управ­ления происходит строго синхронно.

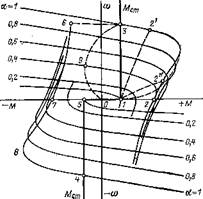
Пусть цикл частотного управления — пуск, реверс н торможение начинается с процесса пуска увеличением ча­стоты статора при включенном на преобразователь непод­вижном двигателе (рис. 4.1, точка О). С возрастанием ча­стоты, т. с. параметра управления а, момент двигателя растет, переходя с одной характеристики a=const на дру­гую при неподвижном двигателе, т. е. |3=0. Когда он пре - 11* 163 высит значение, равное статическому моменту (точка 1), двигатель начинает разбег. В этой граничной точке, как и во всей рассмотренной области неподвижного двигателя, частота ротора равна частоте статора, т. е. а=р, так как угловая скорость ротора оо=0.

С дальнейшим повышением частоты изображающая точка сої, М, переходя с одной характеристики a=const па другую, опишет в плоскости механических характери­стик некоторую кривую — траекторию, для которой время является параметром.

Когда частота достигнет верхнего постоянного значе­ния, например при а=1, траектория изображающей точки выходит на соответствующую механическую характеристи­ку в какой-либо точке, например 2. Далее пуск заканчива­ется при постоянной частоте и изображающая точка 2 пермещается по этой механической характеристике (например, а=1), от граничной точки 2' к точке уста­новившегося состояния 3, где М=Мст, ш=соУст. Положе­ние точки 2', разграничивающей область частотного пуска от области пуска при постоянной частоте, зависит от ско­рости нарастания частоты, т. е. от dfi/dt. В одном пре­дельном случае весьма медленного увеличения частоты точ­ка 2 переходит ИЗ ТОЧКИ 1 В точку 3 ПО прямой М=МСт. 164

В другом предельном случае бесконечно быстрого увеличе­ния частоты скачком до установившегося значения имеем пуск прямым включением и траекторией, изображающей точки в области частотного пуска, является отрезок 1—2 оси абсцисс.

Из рассмотрения траекторий изображающей точки не­трудно установить, что, в зависимости от скорости нара­стания частоты, т. е. от ускорения вращающегося поля двигателя, можно различать два режима частотного пуска: «мягкий» и «жесткий».

При малых ускорениях вращающегося поля весь про­цесс пуска происходит при скольжениях, меньших опроки­дывающего s<Sft (траектория 1—2'), т. е. изображающая точка переходит с одной характеристики a=const па дру­гую, оставаясь всегда на устойчивой ветви характеристики. Такой режим назовем мягким.

При больших ускорениях вращающего поля весь про­цесс частотного пуска происходит при скольжениях, боль­ших критического (s>>sh, траектория 1—2"), т. е. по не­устойчивой ветви характеристик a=const; тогда мы имеем жесткий режим пуска.

Границу между этими двумя областями траекторий да­ет такой режим пуска, при котором изображающая точка переходит с одной характеристики на другую в точках опрокидывающего момента и соответствующего ему сколь­жения Ми, Sk каждой характеристики, описывая траекто­рию 1—2 (рис. 4.1) с параметром а.

Так как в этом граничном режиме, который назвали критическим, момент двигателя имеет максимальное зна­чение при любом значении нарастающей частоты, продол­жительность пуска в области переменной частоты будет минимальной (это еще не говорит о продолжительности всего процесса пуска, поскольку он заканчивается при по­стоянной частоте).

Соответствующий закон изменения частоты во времени и ускорение вращающегося поля будем также называть критическими.

Процесс реверса начинается в точке 3 установившейся скорости прямого направления и кончается в точке 4 прак­тически установившейся скорости обратного направления. Как и в случае пуска, вид траектории изображающей точ­ки зависит от скорости изменения частоты, т. е. от уско­рения вращающегося поля двигателя.

При бесконечно медленном изменении частоты траек­тория проходит по отрезкам М=МСТ через точки З, 1, 0, 5,

4. В другом предельном случае мгновенного изменения ча­стоты с одного значения на другое при обратном следова­нии фаз мы получаем реверс переключением, описываемый траекторией 3, 6, 7, 8, 4. При конечной скорости изменения частоты изображающая точка переходит с одной характе­ристики a=const на другую, описывая некоторую кривую. Если замедление вращающегося поля достаточно велико, машина переходит в генераторный режим с рекуперацией энергии (траектория 3, 9, 0) и замедляется под действием суммы момента машины и статического момента.

Теоретически рекуперативное торможение, подобно пу­ску, возможно и в мягком, и в жестком режимах. Но прак­тически применение жесткого режима торможения ограни­чено вследствие недопустимо больших значений тока и замедление.

В области малых частот момент двигателя уменьшается и обращается в нуль в точке реверса вращающегося поля. При определенных условиях здесь возможна зона непод­вижного состояния в течение некоторого времени.

При дальнейшем нарастании частоты с обратным на­правлением вращающегося поля двигатель переходит в стадию пуска. Ускоряющий момент будет равен разно­сти момента двигателя и статического момента. На этой стадии реверса, как и при простом пуске, возможны оба режима — мягкий и жесткий.

Рассматриваемый цикл заканчивается торможением, ко­торое не отличается от первой стадии реверса. Предельно­му случаю торможения, т. е. при мгновенной остановке вращающегося поля, соответствует динамическое тормо­жение, при котором в статор включается постоянный ток, возбуждающий неподвижное поле.

Аналитическое исследование переходных процессов ча­стотного управления представляет значительные трудно­сти, так как нелинейная задача осложняется наличием двух переменных, в функции которых изменяется момент двигателя: параметра управления а и параметра абсолют­ного скольжения р.

Переходные процессы в общем случае описываются следующей системой уравнений:

М=ф (a, Р);

Параметр частоты а в данном случае управления по разомкнутому циклу является независимой, заданной функ­цией времени.

Подставив в уравнение движения (4.2) угловую ско­рость двигателя со из (4.3), получим одно уравнение

М = Мст + Мп, ш~ - ^11ЮМ|-, (4.4)

в котором динамический момент распадается на две со­ставляющие соответственно двум составляющим скорости. Одна из них

Mia = Uitl0Md^ = Jd^JS

обусловлена изменением частоты статора, т. е. угловой* скорости вращающегося поля. Она равна такому значению динамического момента, которое развил бы двигатель, если бы его ротор разгонялся с постоянным скольжением.

/Щи пуске включением двигателя на напряжение посто­янной частоты первая составляющая равна нулю, а вто­рая имеет знак, противоположный знаку момента двигате­ля и совпадающий со знаком статического момента, так как абсолютное скольжение в этом случае уменьшается. При пуске изменением частоты первая составляющая име­ет знак, противоположный знаку момента двигателя и одинаковый со знаком статического момента, и вторая арифметически суммируется с моментом двигателя, так как абсолютное скольжение растет. Такое соотношение момен­тов объясняется тем, что при пуске с постоянной частотой ускорение ротора достигается только за счет уменьшения скольжения, т. е. за счет динамического момента сколь­жения. При пуске же с переменной частотой ускорение ротора обеспечивается за счет возрастания скорости вра­щающегося поля, увеличивающего запас кинетической энергии ротора, в соответствии с чем синхронный момент и имеет отрицательный знак. Скольжение ротора относи-

167

тельно поля замедляет нарастание скорости ротора и сни­жает темп накопления им кинетической энергии в зависи­мости от динамического момента скольжения, который имеет поэтому один знак с моментом двигателя.

Из сказанного следует, «то синхронный динамический момент можно рассматривать как некоторый фиктивный статический момент, отличающийся тем, что он является независимой функцией времени, заданной законом измене­ния параметра управления а.

На этом основании уравнение (4.4) можно записать в виде

■М = М„' ф •/°))Н0М >

где Мст, ф=Мст+/ш, ііом dajdt — полный фиктивный стати­ческий момент.

Переходные процессы, протекающие в мягком режиме, можно исследовать аналитически, если сделать некоторые допущения, вполне приемлемые для практических целей.

Из рассмотрения механических характеристик рис. 4.1 видно, что все кривые a=const в области малых сколь­жений s<Sft конгруэнтны, а все кривые момента в зави­симости от параметра абсолютного скольжения (рис. 2.4,6) имеют общую касательную с кривой момента при номи­нальной частоте в начальной точке м=0, М—0.

Поэтому, если в мягком режиме пуска ускорение вра­щающегося поля двигателя не превосходит некоторого зна­чения, которое несколько меньше критического gKp, то тра­ектория изображающей точки на плоскости М, р, переходя с одной кривой a=const на другую, остается в окрестно­стях кривой момента при номинальной частоте (а=1) и может быть аппроксимирована некоторой прямой.

Следовательно, момент двигателя в мягком режиме ча­стотного управления можно выразить линейным уравне­нием

М=К$. (4.5)

Пользуясь полученными результатами, рассмотрим про­цесс частотного пуска в простейшем случае линейного из­менения во времени частоты статора (e=const).

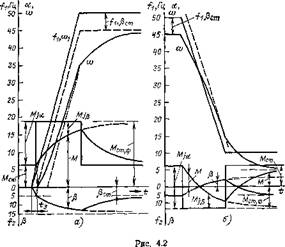
Интегрирование уравнений (4.6) и (4.7) дает следую­щие выражения для пуска при изменении частоты от мо­мента трогания t=t3 (рис. 4.2,а). Параметр абсолютного скольжения (3 изменяется при пуске по закону

Р = М^.± /е (1 _ е~#/Г«>«) _J_ ро^-</Гном> (4 Щ

ДЕ»

где Гном = /соіном5номШном — электромеханическая посто­янная времени, отнесенная к номинальному моменту.

Начальная постоянная определяется из условия, что в момент трогания М^МСТ, а

Окончательно получим:

Р = Ри + £(1-е~'"ио'')- (4.9)

Уравнение скорости согласно (4.3) будет:

<о = е[і_Гно„(1 - е_'/Гно'')|, а уравнение момента двигателя, на основании (4.5)

М = Мст + Уе(1 - e~t/TmM).

После того как частота статора достигнет постоянного, например номинального, значения, пуск будет описывать­ся новым уравнением, которое можно получить из (4.8), подставив в него /е=0, а (3=|3Гр. Если вести отсчет време­ни от новой границы, то получим уравнение

Р = (1 _ e-*/rm«)_i_prpe-"THOU' (4> щ

Значение ргр находится из (4.9):

Ргр = Рст+^(1-^'‘/Гн°'').

где te = -1 ~ -1 = —1-”— (а' — а") — время пуска при изме­

нении частоты, а соїнома' и сошома" — граничная и началь­ная угловые скорости вращающегося поля.

Так как в данном случае скорость ротора

со;=о)1ном (а" |3),

то из (4.10) получим:

—tlT

ш = Шу — (юу — шгр) Є ном,

где o)y=co//i(l—рст) —установившаяся скорость двигателя. 170

Уравнение момента двигателя из (4.5) и (4.10) будет: М — Мст - j - (Mrp— Мст) e~t/Tll0M.

На рис. 4.2,а показаны также кривые момента и пара­метра абсолютного скольжения в зависимости от времени при пуске в мягком режиме. Из этого графика, а также из всего изложенного анализа нетрудно заметить анало­гию между поведением двигателя при пуске повышением частоты и при ударной нагрузке при постоянной частоте.

В нашем случае статический момент играет роль мо­мента холостого хода, а синхронный момент — роль удара нагрузки. Физически это вполне понятно: поведение двига­теля определяется его абсолютным скольжением (и пото­ком). При пуске изменением частоты скольжение увеличи­вается за счет возрастания скорости вращающегося поля, а при ударной нагрузке в случае постоянной частоты —за счет снижения скорости ротора.

Эта аналогия позволяет применять к частотному управ­лению методы теории электропривода при ударной на­грузке.

Закон изменения частоты во времени, обеспечивающий критический режим пуска при максимальном опрокиды­вающем моменте двигателя, можно установить из-уравне­ния движения (4.2). Учитывая, что в критическом режиме М—Мтах> s=sKp. а —sKp), запишем уравнение (4.2)

в виде

do.

^max Л4СТ ~І- ^®іном 0 ®Кр).

Отсюда следует, что искомый закон ^изменения пара­метра управления определяется нелинейным дифференци­альным уравнением

da___ Мтах МСТ _ q

dt /со! НОм (1 sKp)

в котором Мтах и sKp являются функциями параметра а.

В случае торможения изменением частоты (рис. 4.2,6) в уравнении (4.5) меняется знак ускорения вращающегося поля:

М = Мст - 7<о11ЮМ ^ - - Um0M - J-,

т. е. синхронного динамического момента.

Абсолютное скольжение изменяется согласно уравнению

$ = ?СТ-ТНО! Ле(1-е-ІІТП. (4Л1)

Скорость двигателя может быть определена из уравнен ния (4.2), которое теперь примет вид:

(й==(ІИном (и о et—Р) ,

где с/о — начальное значение параметра управления. Подставив сюда р из (4.11), найдем:

« = «'-*[* — Тнт( - е~*1Т™%

где <о'— начальная скорость ротора.

Для момента двигателя получим:

M = MCT-Js(l-e~ilTnov).

В начальной стадии торможения скорость вращающего ся поля больше скорости ротора, т. е. скольжение поле жительно.

Если замедление вращающегося поля и момент инер ции привода достаточно велики, то в определенный мс мент времени скорость поля сравняется со скоростью роте, pa (а=р), а затем станет меньше последней. Скольжени станет отрицательным, и двигатель перейдет в генератор ный режим рекуперативного торможения (см. рис. 4.1,а, б" Если торможение происходит не до полной остановка а до некоторой промежуточной скорости, то с граничног момента, когда частота перестанет уменьшаться и устане вится на постоянном значении a=const, движение буде описываться новым уравнением. Ускорение вращающегос поля обратится в нуль и уравнение (4.11) с новым отсче том времени, примет вид:

Р = РсТ+(Ргр-РОТ)^#/ГнОМ.

где ргр — параметр абсолютного скольжения в гранично^ точке (/=0).

Уравнение для скорости ротора будет:

со =о)" -|— (а)гр — <о") е ^ ||С™,

а для момента

M = Mcr + (Mrv-MCr)e~tlT«™.

При торможении до полной остановки в интервале, ког да частота, а следовательно, и момент двигателя обратят ся в нуль, имеет место режим свободного выбега. Кинети ческая энергия вращающихся масс будет затрачиватьс только на преодоление статического момента, и скорост 172

двигателя будет изменяться по закону

/ /.

На рис. 4.2,6 показаны кривые моментов и абсолютного скольжения при торможении. Синхронный динамический момент (удар нагрузки) в этом случае имеет отрицатель­ное значение. При постоянной частоте такой режим можно получить, если к валу двигателя внезапно приложить из­вне движущий момент, превышающий момент статического сопротивления, под воздействием которого двигатель пе­рейдет в генераторный режим.

Процесс реверса при изменении частоты описывается теми же уравнениями, что и процесс торможения, до тех пор, пока скорость двигателя не достигнет нуля. При ш=0 статический момент меняет знак, и с этой точки переход­ный процесс будет описываться уравнениями пуска с под­становкой в них соответствующих граничных значений.

В жестком режиме пуска є>єкр или при умеренной скорости нарастания частоты, но при больших моментах инерции привода двигатель в процессе разбега выходит в область больших скольжений, близких к опрокидываю­щему моменту или превышающих его. В этом случае из­ложенное выше приближенное аналитическое решение уравнения движения (4.2), основанное на приведении к ли­нейному виду нелинейного уравнения (4.1), неприемлемо и следует использовать ЭВМ.

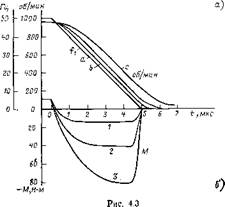
Для иллюстрации различных режимов пуска на рис. 4.3,а приведены кривые угловой скорости и момента двигателя в зависимости от времени ири скорости измене­ния частоты: а — 5 Гц/с, Ь—-10 Гц/с и с —20 Гц/с и при моменте инерции 2,4 кг-м2 или при одной скорости нара­стания частоты 10 Гц/с (шкала времени Ь), но при. раз­личных значениях момента инерции а—1,2, b — 2,4 и с — 4,8 кг-м2.

Из кривых ясно видно, как с увеличением ускорения вращающегося поля частотный пуск приближается к пуску прямым включением.

На рис. 4.3,6 приведены аналогичные кривые торможе­ния для тех же условий (масштабы времени а—5 Гц/с и с — 20 Гц/с не показаны).

т. е. мощность потерь в роторе в мягком режиме управ ления пропорциональна квадрату параметра абсолютное, скольжения.

Следовательно, энергия потерь в роторе в области п^ ременной частоты равна:

Подставляя сюда р из приведенных выше формул, мож­но вычислить потери в рогоре.

С увеличением ускорения вращающегося поля потери растут. Они достигают максимума в предельных случаях прямого пуска, а также торможения противовключением п реверса переключением. Продолжительность переходных процессов соответственно уменьшается. Ускорение выше критического быстро увеличивает потери при незначи­тельном сокращении продолжительности пуска. Для дви­гателей, имеющих специальную форму паза ротора, поло­жение меняется в пользу больших ускорений.

Применение жесткого режима управления ограничива­ется на практике не только экономическими соображения­ми, связанными с потерями, но и с нагревом двигателя, так как токи в жестком режиме в большинстве случаев превосходят допустимые значения и тогда приемлемы толь­ко мягкие режимы.

Область мягких режимов существенно расширяется при управлении по законам поддержания постоянного полного потока (//^-компенсации) и, особенно, постоянного рабоче­го потока.