АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Уравнения равновесия жидкостей
Раздел гидравлики, посвященный изучению покоя и равновесия жидкостей и газов, называют гидростатикой. В случае покоя жидкости силы внутреннего трения отсутствуют и5 следовательно, будучи в равновесии, масса реальной жидкости находится в условиях, близких к идеальной жидкости.
Гидростатическое давление. Внутри жидкости, находящейся в равновесии, можно представить себе элементарную площадку AF. На эту площадку по нормали к ней внутрь жидкости будет действовать сила АР давления столба жидкости. Если бы эта сила была направлена под углом к элементарной площадке жидкости, на которую она действует, то ее можно было бы разложить на две составляющих: направленную нормально и направленную касательно к площадке. Последняя вызвала бы перемещение элемента жидкости и вывела бы жидкость из состояния равновесия.
АР
Силу АР, отнесенную к единице площади, т. е. называют средним гидростатическим давлением.
Предел этого отношения lim =Р будет характеризовать
Напряжение гидростатического давления в данной точке. Последнюю величину в дальнейшем будем называть просто гидростатическим давлением и обозначать буквой р. Д Р
Из отношения следует, что гидростатическое давление измеряется
В единицах силы, отнесенных к единице площади, т. е. в кгс/м2.
Величина гидростатического давления в ка - к о й-н ибудь произвольно взятой точке жидкости не зависит от выбранного направления. Иными словами, как бы мы ни проводили плоскость через данную точку жидкости,
Величина давления на плоскость будет одна и та же. Это положение доказывается при выводе уравнений равновесия жидкости.
Однако гидростатическое давление в. разных точках жидкости будет различным в зависимости от положения этих точек в жидкости.
Давление в точках жидкости, расположенных ближе к поверхности. будет иным, чем в точках, удаленных от этой поверхности. Математически это выражается так: p—f(x, у, г), т. е. гидростатическое давление является в общем виде функцией пространственных координат точки.
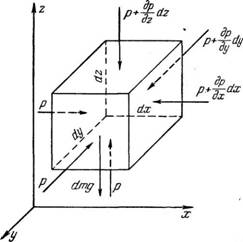
Дифференциальные уравнения равновесия Эйлера. Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед объемом dV с ребрами dx, dy, dz (рис. 1).
Согласно основному принципу статики сумма проекций на оси координат всех сил, действующих на выделенный и находящийся в равновесии параллелепипед, должна быть равна нулю.
В жидкости, находящейся в покое, действуют объемные силы (силы тяжести) и силы гидростатического давления.
Рассмотрим проекции этих сил на ось г. Действие силы тяжести на элементарный объем жидкости пропорционально массе жидкости dm, заключенной в этом объеме, и ускорению силы тяжести g. Сила тяжести направлена вниз и параллельно оси г. Поэтому она будет проектироваться на эту ось со знаком минус:
— Gdm = — PgdV = — Pg dx dy dz
Где p—плотность жидкости.
Сила гидростатического давления, равная pdxdy, проектируемая на ось z, действует по нормали к грани dx, dy. На противоположную грань действует сила, равная
+ Dz^dxdy
Dp j
|
Рис. 1. К выводу дифференциального уравнения равновесия Эйлера. |
Где dz—изменение гидростатического давления в направлении оси г по всей длине ребра dz.
Проекция равнодействующей силы давления на ось г, очевидно, будет равна
Pdxdy — + Dzjdxdy = — ^-Dzdxdy = — DV
И, следовательно, сумма проекций всех действующих сил на ось z равна
-9gdV-^-dV = 0 После сокращения на dV получим
|
Для оси у |
Суммы проекций сил на оси хну будут содержать лишь члены, учитывающие изменение гидростатического давления в направлении соответствующих осей, так как проекции сил тяжести в данном случае равны нулю.
Соответственно получим: для оси х
-•1=0 (1-5)
-1 = 0 (1 5а)
И по предыдущему для оси г
Эти уравнения носят название д ифференциальныхурав- нений равновесияЭйлера. Они определяют условия равновесия элементарного объема жидкости и вместе с тем показывают правильность приведенного выше важного положения гидростатики о том, что гидростатическое давление в произвольно взятой точке жидкости не зависит от выбранного направления.
Указанные уравнения выведены при условии, что элементарный объем жидкости находится под действием силы тяжести, направленной параллельно оси z.
Если сила тяжести направлена под некоторым углом к осям координат, она будет проектироваться также и на оси х и у и в уравнения (1—5) и (1—5а) войдут величины проекции этой силы.
Для того чтобы получить в конечной форме выражение законов распределения гидростатического давления р во всем объеме покоящейся жидкости, необходимо проинтегрировать систему уравнений (1—5), (1—5а), (1—56). Интегрирование приводит к основному уравнению гидростатики, широко используемому в технике.
Основное уравнение гидростатики. В системе дифференциальных „ „ dp dp др уравнении равновесия Эйлера частные производные щ, определяют изменение гидростатического давления в точках, расположенных по направлениям соответствующих осей координат.
Для того чтобы найти изменение гидростатического давления не в точках, а по длине ребер dx, dy и dz элементарного параллелепипеда (см. рис. 1), необходимо, как и при выводе уравнений Эйлера, умножить
Частные производные на соответствующие длины ребер—
Др, . др А. дР. Dx, Dy, Dz: Ах, - щ Ay, ~д - йг.
Совокупность одновременного изменения гидростатического давления в трех направлениях определяет изменение давления во всем объеме жидкости, заключенной в параллелепипеде с ребрами dx, dy, dz, и представляет собой полный дифференциал гидростатического давления:
Dp = ^dx+^dy + ?fzdz
С учетом действия объемной силы (силы тяжести) получим общее выражение закона распределения гидростатического давления в объеме жидкости, заключенной в параллелепипеде с ребрами dx, dy, dz и находящейся в равновесии под действием объемной силы:
Или
* —dp — Pgdz = Q (1—6)
Таким образом, система уравнений Эйлера может быть заменена одним уравнением (1—6).
Для того чтобы определить изменение гидростатического давления во всем объеме покоящейся жидкости, достаточно проинтегрировать это уравнение. С этой целью перепишем его в таком виде:
Pg Dz -J- Dp = О
Но так как то получаем
Dz + ±Dp = 0 (1—7)
Удельный вес несжимаемой однородной жидкости является величиной постоянной, поэтому сумма дифференциалов в уравнении (1—7) может быть заменена дифференциалом суммы
D{z + ^= О откуда после интегрирования получим
Z + у = const = С (1—8)
Константа интегрирования С определяется по известным значениям z и р в какой-либо точке жидкости. Обозначим эти величины через г0 и р0, тогда
И уравнение (1—8) примет вид:
Г + JL^ + fk. (1-9)
Уравнение (1—9) является основным уравнением гидростатики. В нем z и z0—высота погружения двух точек жидкости, р и р0—гидростатическое давление в этих точках.
Уравнение (1—9) можно представить в следующем виде:
Р — Ро
Из уравнения (1—10) следует, что частное от деления гидростатического давления на удельный вес жидкости имеет размерность длины, так как
|
И- |
|
]= |
|
Сила |
|
Сила |
|
Площадь ' объем |
= [длина] = [L] = [м]
Размерность длины имеет также и правая часть уравнения (1—10), выражающая разность высот погружения z0—z:
[Z] = [L]
Правую часть уравнения (1—10), представляющую высоту, соответствующую разности давлений р—р0 при pQt равном давлению на поверхности жидкости, называют пьезометрической в ы с о - т о й.
|
(1-11) |
Закон Паскаля. Решая основное уравнение гидростатики (1—10) относительно величины р, получим:
Р = Ро + 7 (z0 — z)
Из последнего равенства следует, что при изменении давления (р0) в любой точке (z0) жидкости на каку ю-л и - б о. величину давление (р)вовсякой другой точке жидкости изменяется на ту же величину.
Равенство (1—11) является математической формулировкой закона Паскаля, согласно которому давление, производимое на жидкость, заполняющую сосуд, передается во все стороны с одинаковой силой.
Сообщающиеся сосуды. Основное уравнение гидростатики позволяет выяснить условия равновесия жидкости в сообщающихся сосудах.
|
|
|
Л |
|
Рис |
|
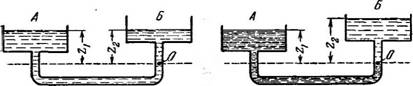
2. Сообщающиеся сосуды, заполненные жидкостью: /—одного удельного веса; II—разного удельного веса. |
|
I |
Пусть два открытых сообщающихся между собой сосуда (рис. 2,/) заполнены однородной жидкостью удельного веса у. Примем некоторую произвольную точку О за начало осей координат. Обозначив ординаты точек, лежащих на поверхности жидкости в сосудах А и Б, через zx и г2, можно для точки О написать: рх = ра + уzx (ра—атмосферное давление), если рассматривать точку О как относящуюся к сосуду А, и р2=Ра + Тгг> если рассматривать ее как точку, относящуюся к сосуду Б.
При наличии равновесия жидкости
|
Pi = P2 Pa +T2i = Pa + T22 |
|
Следовательно отсюда |
Такимобразом, в открытых сообщающихся сосудах заполняющая их однородная жидкость располагается на одинаковом уровне.
Если один из сосудов, например сосуд А, будет закрыт и давление над поверхностью жидкости в нем будет ро, то из условия равновесия рх = р2, и, следовательно,
A)-bTZi = Pa + rZ2
|
Ро Ра |
Откуда
(1 12)
Т. е. в этом случае разность высот уровней в сосудах будет характеризоваться пьезометрической высотой.
Если, наконец, оба сосуда будут открыты, но наполнены различными жидкостями, взаимно нерастворимыми одна в другой, с удельным весом її и Уг» то» располагая точку О на границе между двумя слоями жидкости, как это показано на рис. 2, //, и принимая эту точку за начало осей координат, получим
Pl=Pa + TlZV P2=Pa+ Г 2*2 При условии равновесия, т. е. при р1=р2, имеем
Pa + Llh=Pa + Ї222
Откуда
Її v
Т. е. в этом случае значения высоты уровней жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны удельным весам жидкостей.
Давление жидкости на дно и стенки сосуда. Если жидкость помещена в какой-либо сосуд, то гидростатическое давление на отдельные части площади горизонтального дна сосуда везде одинаково, давление же на боковые стенки возрастает с увеличением глубины погружения; при этом давление на дно сосуда не зависит от формы или угла наклона боковых стенок.
Гидростатическое давление р на уровне дна сосуда при высоте жидкости в сосуде, равной Н, определится следующим образом. .Как было показано выше (1—11):
Р = Ро + ї(2о —
Но
Z0 — Z = Н
И, следовательно,
Р = р0 + тЯ (1-14)
Гдер—давление на дно в кгс/м2\
Ро — давление на поверхности (верхнем уровне) жидкости в кгс/м2; у — уд. вес жидкости в кгс/м3; Н— высота (уровень) жидкости в м.
Общее давление Р на горизонтальное дно не зависит от формы сосуда и объема жидкости в нем. При данном удельном весе жидкости
это давление определяется лишь высотой столба жидкости Н и площадью F дна сосуда:
P = PF Кгс
Или
Р = (р0-|-їЯ)і7 кгс (1—15)
Так как гидростатическое давление жидкости на вертикальную сяенку сосуда изменяется по ее высоте, то общее давление на нее распределяется неравномерно и равно
Р = 7Z) F Кгс (1—15а)
Где z—расстояние от верхнего уровня жидкости до центра тяжести смоченной поверхности стенки; это расстояние зависит от геометрической формы стенки.
Внешнее давление р0 передается жидкостью в одинаковой степени каждому элементу стенки, независимо от глубины его погружения, и, следовательно, равнодействующая внешнего давления имеет точку приложения в центре тяжести поверхности стенки. Давление веса жидкости на вертикальную или наклонную стенку неодинаково по высоте стенки, и чем глубже расположен элемент стенки, тем большее давление веса жидкости он испытывает. Поэтому центр давления жидкости на вертикальную стенку расположен всегда ниже центра тяжести смоченной поверхности стенки.
Центр давления на прямоугольную стенку располагается от верхнего уровня жидкости на расстоянии
С = -|Я (1—156)