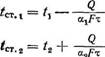АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ

Теплопередача при переменных температурах

Во всех выводах, приведенных выше, предполагалось, что каждая из жидкостей имеет в любой точке поверхности температуру, не изме­няющуюся] ни во времени, ни вдоль поверхности разделяющей стенки. Практически такие условия теплообмена встречаются редко—только в случае, когда одно из веществ, участвующих в теплообмене, является кипящей жидкостью, а другое—конденсирующимся паром. Такой тепло­обмен происходит, например, в выпарных аппаратах, обогреваемых насы­щенным водяным паром.

Обычно температура жидкости изменяется либо по поверхности, оста­ваясь для каждой точки поверхности постоянной во времени, либо одновре­менно и по поверхности и во времени. Первый случай относится к устано­вившемуся состоянию теплообмена, а второй—к неустановившемуся.

Направление іока жидкостей. Теплопередача при переменных тем­пературах в значительной степени зависит от того, в каком направлении вдоль поверхности протекают друг относительно друга жидкости, уча­ствующие в теплообмене.

Практическое значение имеют следующие случаи:

1. Параллельный ток или прямоток (рис. 214, /), при кото­ром обе жидкости, участвующие в теплообмене, протекают вдоль разде­ляющей их стенки в одном и том же

Направлении. ' '

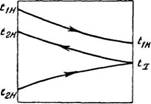
2. Противоток (рис. 214, //), _________ ^ ^________________ 2

При котором участвующие в теплооб­мене жидкости протекают вдоль раз­деляющей их стенки в противополож­ных направлениях.

3. Перекрестный ток (рис. 214, III), при котором жидкости, участвующие в теплообмене, протекают под прямым углом одна относительно Другой.

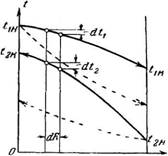
4. Смешанный ток (рис. 214, IV), когда одна из жидкостей про­текает только в одном направлении, в то время как другая жидкость по одну сторону стенки течет в одном направлении, а по другую в об­ратном. Во всех этих случаях температура более нагретой жидкости, от­дающей тепло, уменьшается от начального значения до конечного tlK, а температура менее нагретой жидкости, воспринимающей тепло, увели­чивается от t.2ll в начале до t2K в конце процесса.

Вследствие этого разность температур также будет изменяться от начального ее значения до конечного

Уравнение теплопередачи при параллельном токе жидкостей. Если за время х по обеим сторонам стенки протекают в одном и том же на­правлении с одной стороны более нагретая, а с другой—менее нагретая жидкость и со всех других сторон обе жидкости ограничены теплонепро­ницаемой средой, то теплообмен будет происходить только через стенку.

Температура обеих жидкостей будет изменяться по мере протекания их вдоль поверхности нагрева вследствие теплообмена, но для каждой отдельной точки стенки температура должна быть установившейся.

Пусть стенка, разделяющая жидкости, имеет поверхность F м2 и за время т часов вдоль этой поверхности протекает Gt кгс более нагретой жидкости и G2 кгс менее нагретой.

Обозначим:

Сг и с2—теплоемкость соответственно более нагретой и менее нагретой жидкости в ккал/кгс °С; и t2—температура соответственно более нагретой и менее [нагретой жидкости в °С;

К—коэффициент теплопередачи в ккал! м2- час -°С.

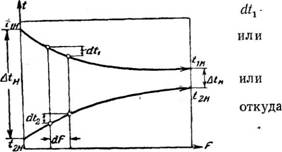
Через элемент поверхности нагрева dF (рис. 215) за промежуток времени х проходит количество тепла:

DQ = Кх (іл — /2) DF

При параллельном токе жидкостей их температуры соответственн® изменяются:

Более нагретой жидкости на dtx= —

Ихс і

Менее нагретой жидкости на dt2—

Знаки минус и плюс в этих уравнениях показывают, что при тепло­обмене температура теплой жидкости понижается, а холодной—повы­шается.

Назовем произведения Gc «водяным эквивалентом» и обозначим

GlCl = Wx

G2c2

1 і 1

Вычитая величину изменения температуры менее нагретой жидкости из величины изменения температуры более нагретой жидкости, получим

MK-ZdF

Обозначив температуры в начале поверхности индексом «н», а в конце—индексом «к» и интегрируя последнее уравнение в пределах от О до F, получим

Vi-h)K F

J =

(H—H)^ О

ИЛИ

ІП ^ік К

Где Л4=^ін——начальная разность температур; Л/к=/1к—t2K—конечная разность температур.

Из этого уравнения получим зависимость разности температур в виде показательной функции

Д Tv = Д Le-M^F-

Где е—основание натуральных логарифмов.

Из уравнения (2—80) следует, что разность температур будет. с течением времени понижаться асимптотически от первоначальной вели­чины Мн до нуля, т. е. до полного выравнивания температур обеих жид­
костей. Это произойдет тем быстрее, чем больше коэффициент тепло­передачи к и поверхность нагрева F и чем меньше водяные эквиваленты и W2, т. е. чем меньше количества жидкостей. После прохождения жидкостей по поверхности F температуры их будут равны и /2К.

Количество тепла, переданное через поверхность F, равно

Откуда

TOC \o "1-3" \h \z _ __________ ------- jl^gK

M~Wl~1~W2 ~ Q

Подставив значение M В ранее выведенное уравнение (Б), получим

, Мк KFx [(/1Н - T1K) + «8к - T№))

Д/н ~ Q

— (4н 4н) (4к 4к)

Или

(4н - О — (4к — UК) = —

И

Q = —KFxUН~А'К = №

1пЖ 1пж

Обозначив среднюю логарифмическую разность температур или средний температурный напор

—д/Г~ =--------------- AFh = /ср - (-г—81)

Нолучим окончательно

Q = KFzAtcp. (2—81а)

Это выражение является уравнением теплопередачи при переменных температурах для установив­шегося состояния процесса в случае параллель­ного тока жидкостей.

Если температура жидкостей вдоль поверхности нагрева изме-

Д/u

Няется незначительно и отношение - г^ <2, то среднюю разность тем-

Нератур А/ср. с достаточной точностью можно определить как средне­арифметическую 0,5 (Д/н4 А/к).

Уравнение теплопередачи при движении жидкостей противотоком. Уравнения (2—81) и (2—81а) остаются верными и для теплообмена при движении жидкостей противотоком. В этом случае при выводе уравнения теплопередачи согласно схеме на рис. 216 следует принять

Dt

°2 Wt

_ J______ 1_

M~Wj w2

Средняя разность температур определяется, так же как и для па­раллельного тока, по уравнению (2—81), причем начальной разностью температур AtH является наибольшая и конечной Д/к—наименьшая разность.

Если G1c1>G2c2, то

^2 к)

Д/,, іЛtо

2н

G2C2>G1C1, то Сін-

А^н = ^2 к

Л/к = /2н

Уравнения теплопередачи при перекрестном токе жидкостей. Расчет процессов теплопередачи при перекрестном токе жидкостей затруднен вследствие сложности ана­литического определения средней разности температур. Для решения технических задач эту разность температур определяют как среднюю разность температур при про­

Тивотоке Д^ср, с теми же начальными и конечными температурами обоих теплоносителей и умножают на поправочный множитель є:

Д^Р; = єД/ср. ,2-82)

Так как поправочный множитель є всегда меньше 1, то средняя разность тем­ператур при перекрестном токе всегда меньше средней разности температур при про­тивотоке.

Значения множителя є приводятся в специальных книгах по теплопередаче [4], В зависимости от вспомогательных величин:

/1н — /1К J Охлаждение горячего теплоносителя

^ ~ T2K'— T2 Н А— нагрев холодного теплоносителя

Чк — А^2 нагрев холодного теплоносителя

^ ~~ /1н — T2H Д£н ~~ разность начальных температур теплоносителей

Наиболее часто при перекрестном токе один из теплоносителей движется раз­дельными потоками (по трубам), а другой—общим потоком (в межтрубном пространст­ве). В этом случае средняя разность температур может быть определена по формуле

Д, пер. = -------------------------------------------------------------------------------------------------------------------------------------------------------------- (2—82а;)

2,318

Где Д^тр. и Д^МТр.—разность температур в трубном и межтрубном пространстве;

ДFH—разность начальных температур теплоносителей.

Уравнения теплопередачи при смешанном токе жидкостей. Теплообмен при сме­шанном токе жидкостей не имеет каких-либо преимуществ по сравнению с противоточ - ным.

Однако если в результате теплового расчета трубчатого теплообменника полу­чают малое число трубок и чрезмерно большую длину их, то для создания более ком­пактного аппарата делают теплообменник многоходовым со смешанным током жид­костей.

Для расчета теплообмена при смешанном токе жидкостей можно пользоваться уравнением

Q = №Д/ср, см.

Где Afcp. См.—средняя разность температур при смешанном токе.

J^ Различают Простой смешанный ток и многократный смешанный Ток.

---- TZH

TZH

TOC \o "1-3" \h \z / N

Рис. 217. Изменение температуры при простом смешанном токе.

В теплообменнике с простым смешанным током жидкостей имеется только один межтрубный ход и несколько трубных.

Теплообменник по схеме на рис. 217 имеет один ход в межтрубном пространстве И два хода в трубном. Более нагретая жидкость дви - ^ жется в межтрубном пространстве, а менее нагретая І2/T

Движется в первом ходе параллельным током и во I " втором—противотоком (рис. 217, /). —

Если изменить направление тока менее нагре­той жидкости, направив ее в первый ход противото­ком, а во второй—параллельным током (рис. 217, //), то она может быть также нагрета до температуры T2K Более высокой, чем конечная температура более на­гретой жидкости T1K.

При простом смешанном токе и четном числе трубных ходов относительное движение жидкостей не влияет на величину Afcp. См.. В случае нечетного числа трубных ходов а^ср. см. выше, если число про - ,тивоточных ходов больше, чем параллельноточных.

При простом смешанном токе для подсчета средней разности температур можно пользоваться уравнением В. С. Яблонского

(*1Н — Ьк) + (кк — *2н) + V (TlK — T1K)2-H (^к —?2н)2

- к) ~Ь у (кн ^ік)2 Ф (T2K------ ^2н)2

Многократный смешанный ток применяют в тех случаях, когда в теплообменнике межтрубное пространство, так же как и трубное, имеет несколько ходов. При многократном смешанном токе обе жидкости при движении через тепло­обменник несколько раз изменяют свое направление (рис. 218).

Среднюю разность температур при многократном смешанном токе определяют по уравнению

U + / (T1H - *1К)2 -F (T2K - T^F

(гда N—число ходов в межтрубном пространстве) и

N

Ь = №,„ - Uk) - «« - WJ Y^izM

N

/ ('ін — 4к) — V(t* к — ^ян)

При любом варианте смешанного тока средняя разность температур меньше, чем при противотоке, но больше, чем при параллельном токе. Если в процессе теплообмена температура одного из теплоносителей остается постоянной, то средние разности темпе­Ратур для противотока, параллельного и смешанного тока не будут отличаться друг от Друга.

Выбор направления тока жидкостей. В тепловых процессах с уста­новившимся тепловым режимом изменение температур жидкостей может происходить следующим образом.

1. Обе жидкости, участвующие в теплообмене, имеют постоянную температуру как по поверхности теплообмена, так и во времени. Такой случай наблюдается, например, когда по одну сторону разделяющей стенки происходит конденсация насыщенного пара, а по другую нахо­дится кипящая жидкость.

2. Одна из жидкостей, участвующих в теплообмене, имеет в тече­ние всего времени протекания процесса теплообмена постоянную темпе­ратуру, а температура другой изменяется от tH до tK.

3. Температура обеих жидкостей изменяется при любом направле­нии их движения вдоль разделяющей стенки.

В первых двух случаях теплопередача и расход теплоносителя не зависят от того, будут ли жидкости направлены параллельно, противо­током, перекрестным током или смешанным током, так как это не отра­зится ни на температурах, ни на разности температур. Поэтому напра­вление тока жидкостей выбирают, исходя только из конструктивных и технологических соображений.

Когда температура обеих жидкостей в процессе теплообмена изме­няется, то направление их движения будет существенно сказываться на процессе теплообмена и прежде всего на конечной температуре жидко­стей. При изменении конечных температур будут изменяться разность температур и расход теплоносителя.

Наиболее расходящиеся результаты получаются при сравнении параллельного тока с противотоком.

Обозначим:

Gt и G2—количество теплой и холодной жидкости в кгс; сх и с2—удельная теплоемкость их в ккал/кгс-°С; t1H и t1K—начальная и конечная температура теплой жидкости в °С; и —начальная и конечная температура холодной жидкости в °С.

При отсутствии потерь тепла, по закону сохранения энергии, должно соблюдаться равенство

= G2C2 (t2К 4н) = Q из которого можно найти расход теплой жидкости при нагревании:

Q __ Gypz (^2 К ^2н)1 _ ____ Q_____

1 TOC \o "1-3" \h \z СІ — ^ік) СГ —

Или расход холодной жидкости при охлаждении: Q __ GlCl (*1Н — _ Q

2 С2 0-2К. ^2н) С2

Из последнего уравнения следует, что при заданных значениях ^і» hm і\к и расход охлаждающей жидкости G2 зависит только от конечной ее температуры t2K: с увеличением конечной температуры рас­ход охлаждающей жидкости будет уменьшаться и, наоборот, с пониже­нием температуры—увеличиваться.

Температура жидкости t2K при параллельном токе всегда меньше tlK, в то время как при противотоке t2K может быть больше t1K, приближаясь как к пределу к Таким образом, при противотоке расход охлаждаю­щей жидкости в процессе охлаждения или нагревающей жидкости в процессе нагревания может быть меньше, чем при параллельном токе.

Сокращение расхода охлаждающей или нагревающей жидкости при противотоке достигается обычно некоторым уменьшением средней разности температур, а следовательно, и увеличением потребной поверх­ности теплообмена.

Однако экономия от снижения расхода теплоносителя при противо­токе всегда значительно превышает дополнительные затраты на изго­товление аппарата больших размеров, который может потребоваться в случае противотока. Если конечную температуру охлаждающей жидко­сти при противотоке принимают такой же, как и при параллельном токе, то расход теплоносителя остается в обоих случаях одинаковым, разность же температур будет большей при противотоке.

Поэтому при непрерывно изменяющихся температурах теплоноси­телей всегда следует устанавливать теплообменники, работающие по принципу противотока.

Перекрестный и смешанный токи жидкостей занимают по разности температур и расходу теплоносителя промежуточное положение между параллельным током и противотоком. Выбор перекрестного или смешан­ного тока диктуется не экономическими, а только конструктивными соображениями.

Температура стенок. Для расчета теплового потока в процессах теплопередачи надо знать температуру, которую будет иметь стенка, раз­деляющая жидкости. Это требуется также для вычисления потерь тепла стенками аппаратов в окружающую среду.

Количество передаваемого тепла для обеих сторон стенки находят по уравнениям

Q = Ct^Fx — TcТ. х) и Q = A2Fx (T„M 2 — T2)

Из этих уравнений можно определить температуру стенок, а именно:

Подставив вместо Q его значение из уравнения теплопередачи

Q = KFxMcp.

Получим

[ ____ 1 __ Лгта<ср.

Ст'1 — 1 a1Fz~

И

4т.2---- 4

Откуда окончательно

(2—86)

(2—87)

Температура стенки всегда ближе к температуре теплоносителя с большим коэффициентом теплоотдачи.

Средняя температура теплоносителей. При расчете коэффициентов теплоотдачи необходимо знать среднюю температуру теплоносителя с каждой стороны стенки. Если процесс теплообмена происходит при изменении агрегатного состояния одного из теплоносителей (конденса­ция, кипение), то его температура остается неизменной вдоль поверх­ности нагрева ^lcp.=/1=const, а среднюю температуру второго тепло­носителя находят по формуле

^іср. — ср. = д*ср. (2—88)

В общем случае средняя температура теплоносителей при неизмен­ном агрегатном их состоянии с обеих сторон поверхности нагрева может быть определена по формулам, предложенным Е. Я. Соколовым: » для противотока

V ____ Rt^K Д^ср. - Ь /О Qrv\

2ср.------------------- і-------------------- v-—

Для прямотока

/ • _____ — Д^ср. "Ь /о ОЛ\

2ср. —--------- /Г+Т----------------------------------------- ' — '

Где

£) _ G2C2 ____ І1и — TiK

Определение поверхности нагрева при переменных теплоємкостях и переменных коэффициентах теплопередачи. При выводе формул для определения средней разности температур теплоемкости участвующих в теплообмене веществ и коэффициенты теплопередачи были прибли­женно приняты постоянными.

Если теплоемкость и коэффициент теплопередачи значительно (более чем в два раза) изменяются в заданном интервале температур, то поверхность теплообмена F определяют методом графического инте­грирования из общего уравнения теплопередачи:

Р __tP Glc1dt J K(h-k)

*ік

Принимая ряд промежуточных значений t2 между t2li и t2K, опре­деляют по тепловому балансу соответствующие им значения tlt а также

Величины с и К и строят кривую — . - в зависимости от t2. Пло-

А Г2) *

Щадь, ограниченная кривой, осью абсцисс и ординатами, соответствую­щими t2н и t2K, равна величине F.

Аналогично можно вести расчет, приняв ряд значений tx.

Уравнения теплопередачи для неустановившегося процесса теплообмена, В тех

Случаях, когда процесс теплообмена проводится периодически, т. е. когда вся нагре­ваемая или охлаждаемая жидкость помещена в одном сосуде и обменивается теплом с другой жидкостью, протекающей вдоль разделяющей их стенки, процесс теплопередачи будет неустановившимся и температуры меняются непрерывно вдоль поверхности и во времени.

Средняя разность температур обеих жидкостей здесь уже не может быть вычис­лена обычным способом, так как конечная температура непрерывно протекающей жид­кости будет изменяться в течение всего процесса теплообмена. Примером одновремен­ного изменения температур как во времени, так и по поверхности может служить про-
несс теплообмена при охлаждении неподвижной (или перемешиваемой при помощи ме­шалок) жидкости в сосуде холодной водой, непрерывно протекающей по змеевику.

Рассмотрим метод расчета теплообмена при неустановившемся состоянии про­цесса для случая охлаждения жидкости (предложен Г. П. Питерским). Обозначим:

Tm—начальная температура охлаждаемой жидкости; Чк—конечная температура охлаждаемой жидкости; t2n—начальная температура охлаждающей жидкости; *2к—конечная температура охлаждающей жидкости; t—температура охлаждаемой жидкости в любой момент; *2ср. к—средняя конечная температура охлаждающей жидкости; <?i—количество охлаждаемой жидкости в кгс; Сх—теплоемкость охлаждаемой жидкости в ккал/кгс°С; G2—расход охлаждающей жидкости в кгс; с2—теплоемкось охлаждающей жидкости в ккал1кгс°С; G4—часовой расход охлаждающей жидкости в кгс/час\ К—коэффициент теплопередачи в ккал/м2-час'°С; F—поверхность теплопередачи в ж2; т—продолжительность процесса теплообмена в час. Начальные и конечные температуры обеих жидкостей являются заданными. За промежуток времени dx на нагрев охлаждающей жидкости будет затрачено

Тепла

DQ = G4C2 (T2K — Tw) Dt

Это количество тепла должно пройти через стенку и, следовательно, может быть выражено так:

DQ = K^Tcv.Fdx

Где

1ПАГк

Для любого момента теплопередачи:

Начальная разность температур A tn~t—12 н Конечная разность температур htK—t—t2K Подставив эти значения в выражение средней разности температур, получим

• ^>н) № ^2к) Агк

"£г п. —

T -- Tav T Ta

При этом уравнение теплопередачи принимает вид

DQ — KF —7і Di = G4c%(t2K — t2K) dx In

T~ U

Откуда

T~ tjK _ KF

К G4C2

KF

При заданных условиях теплообмена величина q ^ является постоянной и следовательно,

T—t.

= const = А

T — t2

Из последнего равенства

T(A — 1) + T2Li

'2К — J^

Количество тепла, отдаваемое более нагретой жидкостью за любой промежуток времени Dx, равно

-GlCldt = KF

Подставив найденное значение T2K, получим

Г Л KF[t{A-\) + tm-At2V\ ,.„-4-1 .. . . . ~GlCldt= ЛІЇЇЛ ^ =

Dt _ Л — 1

" T — T2H~ A In AG& Интегрируя последнее уравнение в пределах от 0 до т и от T1H До T1K , получим

U

Dt _ KFi А — 1 T — *2н Gjq Л In Л

1Н

KFx A - 1

ІП

— *2H <Vi Л In Л

Откуда, умножая обе части уравнения на величину (F1H—T1K) И производя соответствую­щие преобразования, найдем

Q,= GlCl (Fte - /1к) = №--------------- TlH-T2„ ША

In T

Следовательно, в данном случае уравнение теплопередачи имеет вид:

Q = KFzAt'cp (2-91)

Где

TlH — t1K А 1

СР-~ 11H— t2n 2,ЗА \gA

T-TK T,

Общий расход охлаждающей жидкости равен

Q

G2 = —J;---------------------------------------------- R-т- кгс (2—92)

С2 \2Ср. К С2Н/

Причем средняя конечная температура T2Ср. к определяется следующим путем.

Для всего процесса охлаждения соответствует уравнение теплопередачи

Q = ОчС2 (t2cp. к - U * = KFM'^т (б)

Следовательно,

KFAt'

F _________________________ F — _______

*2ср. к 2ч — G4c2

Из приведенного выше равенства (а) следует

1--- Нк "4С2

Подставив это значение в уравнение (б), получим

4ср. к 4н = 1П

Откуда

^2ср. к = Д*ср. ІП Л + t2li (2-93)

Распространяя предыдущий вывод на теплообмен с неустановившимся состоя­нием процесса при Периодическом нагревании, аналогичным путем найдем

Д = ^ — T

Где —начальная температура греющей жидкости; T1K—конечная температура греющей жидкости; T—температура нагреваемой жидкости в любой момент.

Примем обозначения: <2н—начальная температура нагреваемой жидкости: /2к—конечная температура нагреваемой жидкости

Тогда средняя разность температур для всего процесса нагревания может быть определена по формуле

Лі' -------- -------- — *2Н___________ Л — 1 /О__ СЛ\

^-"n o1rT —**н 2, ЗЛ • lg Л ^ Ь4>

2,3 lg 7--------- г-

'1Н *2К

А средняя температура греющей жидкости

Tlcp. = TlK — Ltcp.\NA (2-95)

Потери тепла в окружающую среду. Во всяком тепловом процессе возникают потери тепла вследствие теплообмена между нагретыми поверхностями стенок аппаратов и окружающим воздухом.

Потери тепла в окружающую среду могут быть определены сум­мированием результатов двух самостоятельных процессов: перехода тепла в окружающую среду путем конвекции и путем теплового излу­чения.

Так как температура стенок в процессе потерь тепла в окружаю­щую среду будет выше температуры воздуха, то уравнение теплоотдачи можно написать следующим образом:

Q = (4Т.2 — 4озЛ.) ккал (2—96)

Где у.2—коэффициент теплоотдачи от стенки к воздуху, равный сумме коэффициентов теплоотдачи конвекцией ак и тепло­отдачи лучеиспусканием ал> т. е. а2=а к+;л ккал/м2- час-°С;

Uт.2—температура наружной стенки;

4озд.—температура окружающего воздуха.

Числовое значение коэффициента теплоотдачи ак от стенки к окру­жающему воздуху, находящемуся в состоянии естественной конвекции, определяют по уравнениям (2—60) и (2—61). Для приближенных рас­четов уравнения (2—60) и (2—61) упрощают подстановкой в них средних значений физических констант для воздуха и подбором коэффициентов пропорциональности опытным путем.

При температуре стенки 50—350° применима приближенная фор­мула, предложенная В. П. Линчевским

А2 = 8 + 0,05/Ст.2 ккал! м2-час -°С (2—97)

Для воздуха, движущегося вдоль плоских шероховатых стенок (вынужденная конвекция), можно приближенно принимать: при м/сек

Ак = 5,3 + 3,6ш ккал/м2 ■ час ■ °С (2—98)

При <^>5 м/сек

Ак = 6,7 W0'™ Ккал/м ■ час-°С (2—99)

Где w—скорость движения воздуха в м/сек.

22 А. Г. Касаткин.