АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ

Смеси паров с газами

Основные понятия. Если какая-либо жидкость находится в соприкос­новении с газом, то образующийся при испарении жидкости пар будет смешиваться с газом с образованием однородной (до определенного пре­дела) газовой смеси. Полное насыщениЕ газа парами жидкости произойдет ТОгда, когда парциальное давление паров в смеси станет равным упругости" насыщенного пАра жидкости при данной температуре.

- Обозначим: ' "*""' ——-------------------- —*

Ун—уд. вес насыщенного пара в кгс/мг\ Тг—УД - вес сухого газа в кгс/м3-, уп—уд. вес пара, находящегося в газе, в кгс/м3-, Рн—упрУгость насыщенного пара данной жидкости в кгс/м2-, Рп—парциальное давление паров жидкости во влажном газе в кгс/м2\ РГ—парциальное давление сухого газа в кгс/м2-, ' Р—общее давление влажного газа в кгс/м2-, Т—температура влажного газа в °К; Rr—газовая постоянная сухого газа в кгсм/кгІК', Rn—газовая постоянная паров жидкости в кгсм/кг\К; t—температура влажного газа в °С; сп—теплоемкость перегретого пара в ккал/ кгс°С\ сГ—теплоемкость сухого газа в ккал/кгс°С; /—теплосодержание влажного газа в ккал/кгс сухого газа; і—теплосодержание пара при данной температуре в ккал/кгс-, г0—теплосодержание пара при 0°С в ккал/кгс.

Рассмотрим основные свойства влажного газа: влажность, влаго - содержание, теплосодержание.

Различают абсолютную и относительную влаж­ность газа.

Абсолютная влажность газа. Абсолютной, или объемной, влажностью газа называется вес водяного пара, содержащегося в 1 м3 влажного газа. Объем пара равен объему влажного газа, и поэтому абсолют­ная влажность равна удельному весу водяного пара в смеси—уп кгс/мв.

Относительная влажность газа. Относительной влаж­ностью, или степенью насыщения газа влагой, называется отношение веса водяного пара, содержащегося в 1 ж8 влажного газа, к максимально возможному его весу при данных условиях (при той же тем­пературе и том же общем давлении).

Максимально возможным содержанием пара в 1 ж3 влажного газа является вес 1 м3 насыщенного пара при данных значениях температуры и давления, равный ун. Следовательно, относительная влажность

Ср = —- (3—323)

По уравнению состояния идеальных газов

_L _ _

V Ї RT

Удельные веса могут быть выражены следующими формулами:

7 = Рп и Т = Гп RnT Тн япг

Принимая приближенно, что для парогазовой смеси действительно уравнение состояния идеальных газов и подставляя полученные значе­ния у в выражение относительной влажности, получим

' RnT • RnT

Откуда

? = - Г" (3-324)

Из уравнения (3—324) видно, что относительная влажность газа мо­жет быть выражена отношением парциального давления паров жидкости, находящихся в газе, к давлению насыщенного пара той же жидкости при данной температуре.

Если заданы температура и давление газа, то относительная влаж­ность однозначно определяется величиной Рп парциального давления пара в газе. Так как последнее может изменяться в пределах от Рп—0 до РП=РН. то

Тмакс. ~Ъ ^

Влагосодержание газа. Вес пара жидкости, приходящейся на 1 кгс сухого газа, .называется влагосодержанием газа.

Влагосодержание газа

Подставив в это выражение значение уп и уГ из уравнения состоя­ния идеальных газов, получим

__ РП. ^г ________ RrPn

По закону Дальтона и из уравнения (3—324)

Рп = <?Р»

Подставив эти значения Рг и Рп, получим

<3-325>

Влагосодержание газа при заданных величинах * температуры и давления однозначно определяется значением <р и, следовательно, может

Изменяться от хмин. ==§■ =0 до хмакс. = §-г Рн

RnP—0 Лмакс- Rn Р—Рн'

Если температура газа достигает температуры кипения данной жидкости, то Рн—Р и, следовательно, х=<х>, т. е. газовая фаза будет состоять лишь из одного компонента—насыщенного пара, и испарение переходит в кипение жидкости.

В частном случае, когда жидкостью является вода, а газом—воз­дух, газовые константы имеют следующие значения: R=29,27 кгсм! кгс°К,

Rn=47,06 кгсмікгс0К и = ^0,622.

Соответственно влагосодержание воздуха:

Х = 0,622 (3—326)

£н

Теплосодержание влажного газа. Теплосодержание влажного газа определяется суммой теплосодержаний сухого газа и паров влаги, находя­щихся в нем. Относя теплосодержание влажного газа к 1 кгс сухого газа, получим уравнение

/ = CTt + Зсі Ккал/кгс (3—327)

Для влажного воздуха, содержащего пары воды сг = 0,24 ккал/кгс-°С / = 595л: + 0,46/

Где 595 Ккалікгс—теплосодержание водяного пара при 0° или, что то же самое, теплота парообразования воды при 0°С. Подставив значение сГ и і в уравнение (3—327), определим теплосо­держание влажного воздуха

I = 0,24* + 0,46л;/ + 595/ (3—327а)

Или

/ = (0,24 + 0,46л:) / + 595х (3—3276)

Точка росы. При охлаждении влажного газа с постоянным влаго - содержанием х степень насыщения газа парами жидкости может достиг­нуть величины ср=1 и тогда газ становится насыщенным парами жид­кости. При дальнейшем понижении температуры пар, находящийся в газе, конденсируется и влагосодержание последнего будет уменьшаться.

Температура, при которой газ данного состояния, охлаждаясь при постоянном влагосодержании, становится насыщенным, называется точ­кой росы. Эта температура является пределом охлаждения влаж­ного газа.

Точку росы можно определить из уравнения (3—325). Принимая Ф = 1, получим:

У_ Rr Р»

Х~ Rn Р-Рн

Обозначая ^г через а и решая это уравнение относительно Рн, нахо-

■•Mi

Дим упругость насыщенного пара данной жидкости, соответствующую точке росы:

Рг. р.-^ (3-328)

По найденному значению Ртф. определяют температуру жидкости (по таблицам). Эта температура и будет точкой росы. Уравнение (3—328) показывает, что при постоянном давлении Р точка росы однозначно опре­деляется влагосодержанием и не зависит ни от температуры, ни от сте­пени насыщения газа влагой.

Для смеси воздуха с парами воды а=0,622 и, следовательно

Р*-1>- = оЖ+1с_ <3~328А>

Температура мокрого термометра. При взаимодействии газа с жид­костью в адиабатических условиях, т. е. без подвода и отвода тепла извне, газ насыщается парами жидкости, охлаждаясь при постоянном тепло­содержании.

Пределом охлаждения газа будет температура, соответствующая его полному насыщению (<р=1). Температура, при которой газ, охлаж­даясь при постоянном теплосодержании, становится насыщенным, на­зывается температурой мокрого термометра или тем­пературой предела охлаждения влажных тел. При этой температуре тепло, переходящее от газа к смоченной поверхности, полностью затрачивается на испарение жидкости, а температура последней остается постоянной и находится в пределах между температурой газа и температурой мокрого термометра.

Пусть t и х—температура и влагосодержание газа данного состоя­ния, a tM и хн—температура и влагосодержание этого же газа после охлаж­дения его при постоянном теплосодержании до температуры мокрого термометра.

Тогда можно написать равенство

(сг +X)K:+V0x = (сгШ^Ж+У0хИ (3-329)

Где г0—теплосодержание паров данной жидкости при 0°С.

В уравнении (3—329) два неизвестных—їмихн, причем величина х является функцией tu. Поэтому числовое значение tM находят путем иод - бора. Определяя ряд значений х в зависимости от tM по формуле (3—329), подставляют значения хн и tM в уравнение (3—329) до получения тож­дества. Числовое значение tM, соответствующее этому тождеству, будет температурой мокрого термометра или предела охлаждения влажных тел.

На практике величину tu определяют непосредственно, измеряя тем­пературу данного газа при помощи так называемого мокрого термометра, у которого шарик со ртутью обернут марлей или кисеей, которая по­стоянно смочена жидкостью. Прибор, состоящий из мокрого и сухого термометра (психрометр), позволяет определить фактическое со­держание влаги в газе.

Значения tM, как и других параметров, характеризующих состоя­ние влажного воздуха, могут быть легко определены графически по /— х-диаграмме для влажного воздуха.

Объем и вес влажного газа и воздуха. Влажный газ как паро-газовая смесь занимает тот же объем, что и каждая составляющая этой смеси, но находящаяся под давлением, равным парциальному давлению данной состав­ляющей. Поэтому объем влажного газа определяют обычно по объему абсо­лютно сухого газа.

Обозначим:

Тг—удельный вес сухого газа при данных температуре и давлении в кгс/м3;

Тог—удельный вес сухого газа при 0° и 760 мм рт. ст. в кгс/м3;

Тп—удельный вес паров влаги, находящейся в газе при данной темпе­ратуре и давлении, в кгс/м3;

Топ—удельный вес паров влаги при 0° и 760 мм рт. ст. в кгс/м3; ^вл. г—объем влажного газа в м3/кгс сухого газа;

Vr—объем сухого газа в м3/кгс сухого газа.

Объем влажного газа можно выразить следующим равенством:

И _____ 17 І Т Юззо

^ВЛ - Г ^гц Yor 273 Р— Рп

Пли

^вл. г = 37,8 7ог {РТ_ рп) кгс/м3 сухого газа (А)

*

§При расчете сушилок обычно бывает известно влагосодержание х, а не Рп. Поэтому следует выразить объем влажного газа в зависимости от влагосодержания. По предыдущему влагосодержание выражается отношением

(Б)

Удельные веса пара и газа при данных условиях температуры и давления можно выразить через удельные веса при 0° и 760 мм pm. ст.

— Рп

Тп Топ у Р

__ 273 Р — Рп

Тг Тог у Р

Подставляя эти значения удельных весов газа и пара в отношение (Б), получим

__ Топ_____ Рп

Тог. 'Р-Ріі

Или, имея в виду, что уоп=0,804 кгс/м3:

0,804 Рп Топ \P-Pn

42 д г Касаткин.

Из последнего равенства находим

Рх

0,804

Ij -JUL- ^

(В)

Yon

По значению Рп из равенства (В) можно найти

0,804

TOC \o "1-3" \h \z Р_р P_r, X Yor

0,804 0,804

Yon Yor

Подставляя найденное значение Р—Рп в уравнение (А), получим

/ 0,804 \

37'8Т("ІьГ + л7 ^вл. г= 0 804Р $—330)

Удельный вес сухого воздуха при 0°и760лш рт. ст.—у0.в.= 1,293, поэтому объем влажного воздуха можно выразить формулой:

Квл. в = 47 Т {0'62р + х) кгс/м3 (3—330а)

Вес 1 м8 влажного газа можно найти путем деления 1+* на VM. r:

Тв, г=---- f0(1804^ N (3-3306)

47ТЫг + х)

А вес 1 ж8 влажного воздуха

Кес, м3 (з-ззов)

Диаграмма /—х состояния влажного воздуха. Аналитический ме­тод расчета сушилок весьма сложен. Более простым является графи­ческий метод расчета при помощи I—d-диаграммы влажного воздуха, предложенной Л. К - Рамзиным. Для облегчения технических расчетов в /—х-диаграмме (рис. 456), в отличие от диаграммы Рамзина, влаго­содержание d воздуха выражено не в г/кгс воздуха, а в кгс/кгс сухого воздуха и обозначено через х.

Диаграмма построена в косоугольной системе координат (угол между осями координат равен 135°). По оси абсцисс диаграммы отло­жены величины влагосодержания воздуха х, а по оси ординат—его удель­ного теплосодержания I. Диаграмма составлена для барометрического давления 745 мм pm. ст. \

На /—%-диаграмме нанесены линии постоянного влагосодержания, постоянных температур (изотермы), постоянного теплосодержания, по­стоянной относительной влажности и парциального давления йодяных паров.

Линии постоянного влагосодержайия. Для удобства пользования диаграммой (см. рис. 456) величины влагосодержа­ния нанесены на вспомогательной горизонтальной оси, проходящей через начало координат. Шкала принята в определенном масштабе для влаго­содержания от 0 до 0,15 кгс/кгс абсолютно сухого воздуха. Вертикали,

-проходящие через точки оси абсцисс, представляют собой линии постоян­ного влагосодержания.

Линии постоянной температуры. По оси ординат диаграммы нанесены температуры от —10 до +200° и проведены линии постоянных температур (изотермы), соединяющие точки постоянной тем­пературы при разных значениях lux.

По оси ординат отложены также в определенном масштабе величины теплосодержания 1 кгс абсолютного сухого воздуха сс. в t^ 0,24/ ккалікгс.

При определенном влагосодержании х расстояние по вертикали от изотермы t до оси абсцисс равно

I = Сс. в t + сПхі = 0.24і + 0,46х/ + 595А-

Изотермы представляют собой линии, близкие к прямым, но на­клоненные к вспомогательной горизонтальной оси.

В связи с тем, что теплосодержание водяного пара возрастает с температурой, наклон изотерм увеличивается по мере возрастания тем­пературы.

Линии постоянного теплосодержания. Состояние влажного воздуха определяется точкой пересечения изотермы t с ли­нией постоянного влагосодержания х. Теплосодержание влажного воз­духа, содержащего 1 кгс сухого воздуха и х кгс пара, определяется расстоянием от точки, характеризующей состояние воздуха, до оси абсцисс, т. е. величиной \

I + +

Причем слагаемое 595х предсУшЛ^е^ собой расстояние по линии постоян­ного влагосодержания х от оси абсцисс до изотермы /= 0.

Линии постоянного теплосодержания представляют собой прямые, проведенные параллельно оси абсцисс.

Линии постоянной относительной влажности. Эти линии представляют собой кривые, которое наносят на диаграмму через точки пересечения изотерм t с влагосодержанием х, найденным при данных значениях t и <р согласно уравнению

Х(If «= Const) — Р _ Yp^v

При постоянном значении у—1 находят величины х для ряда тем­ператур. Точки пересечения линий х с соответствующими им темпера­турными линиями (изотермами) являются точками, лежащими на ли­нии <р= 1; соединяя их, получают кривую <р=1. Таким же образом находят точки пересечения температурных линий с линиями х, найденными по приведенному выше уравнению при ср=0,9, и через найденные точки проводят кривую ср=0,9 и т. д.

Кривые rp=const имеют резкий перелом при температуре 99,4°, соответствующей общему давлению 745 мм рт. ст., и направлены верти­кально вверх. Это объясняется тем, что диаграмма построена для суши­лок, работающих при атмосферном (барометрическом) давлении, равном 745 мм рт. ст. В этих условиях при ^>99,4° упругость насыщенного водяного пара, находящегося в воздухе, будет равна общему давлению, т. е. Pf^P' и согласно уравнению (3—71)

*= - 0.622^-

Это означает, что при температуре 99,4° влагосодержание воздух? при данной относительной влажности остается постоянным.

Линия ср = 1 соответствует полному насыщению воздуха влагой при данной температуре. Выше линии насыщения находится область не­насыщенного влажного воздуха, а ниже — область, в которой водяной пар частично конденсируется из воздуха.

Линии парциальных давлений пара. Эти линии проводят через точки величин парциальных давлений водяного пара Рп, вы­численных по формуле

П 0,622 4-х

Эта формула получается из уравнения (3—326), если решить его относи­тельно Рп.

Из последнего выражения видно, что при данном общем давлении парциальное давление зависит только от х, т. е. для одного и того же влагосодержания х парциальное давление пара является величиной по­стоянной, не зависящей от температуры и степени насыщения воздуха. Для реального газа величина х зависит и от температуры. Поэтому сде­ланный выше вывод является не совсем точным, но допустим для техни­ческих расчетов.

Парциальное давление водяного пара определяется на диаграмме точкой пересечения линии A;=const с кривой парциального давления. Значения парциального давления водяного пара нанесены на правой оси ординат диаграммы.

Состояние влажного воздуха характеризуется на /—х-диаграмме пересечением четырех линий: постоянной температуры (изотермы), постоянного влагосодержания, постоянной относительной влажности и постоянного теплосодержания.

Для определения состояния воздуха должны быть заданы любые два параметра, по которым могут быть определены и остальные.

При помощи /—^-диаграммы можно также определить точку росы (предел охлаждения воздуха) и температуру мокрого термометра (пре­дел охлаждения влажных тел).

Точка росы. Для расчета процессов сушки важно знать точку росы, т. е. температуру, при которой воздух данного состояния, будучи охлажден при постоянном влагосодержании, полностью насыщается вла­гой. На диаграмме точка росы /рос. для воздуха данного состояния опре­деляется изотермой, проходящей через точку пересечения линии задан­ного влагосодержания с линией 9 = 1.

Предел охлаждения влажных тел, или темпе­ратура мокрого термометра. Выше было указано, что испарение влаги из материала в воздух может происходить в адиабати­ческих условиях только вследствие охлаждения воздуха (при повышении его влагосодержания и неизменном теплосодержании). При этом темпе­ратура влажного материала будет понижаться до некоторого предела охлаждения, который соответствует полному насыщению воздуха влагой (9== 1) и равенству температур влажного материала и воздуха.

Предел охлаждения влажного материала соответствует темпера­туре мокрого термометра и может быть определен по I—х-диаграмме.

На диаграмме температуру предела охлаждения tM находят как изотерму, проходящую через точку пересечения линии постоянного теплосодержания (7=const) воздуха данного состояния с линией 9=1. Линии /M=const являются геометрическим местом точек с одинаковой температурой мокрого термометра; эти линии идут несколько менее круто, чем линии I = const. \

107. Материальный и тепловой балансы воздушной сушилки

Принцип действия воздушной сушилки. При сушке в токе воздуха или газа теплоноситель, соприкасаясь с поверхностью влажного мате­риала, поглощает из него некоторое количество влаги и удаляется из сушилки.

В качестве теплоносителей для сушки применяют главным образом предварительно нагретый воздух и дымовые газы.

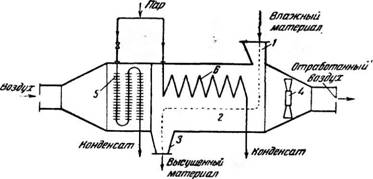
Схема сушки в токе воздуха показана на рис. 457. Влажный материал поступает через загрузочную воронку / и при помощи транспортных

Приспособлений продвигается вдоль сушильной камеры 2; после сушки материал удаляется через воронку 3. Вентилятором 4 в калорифер 5 Засасывается холодный воздух; здесь он подогревается до определенной температуры и за|тем проходит вдоль сушилки. Соприкасаясь с высуши­ваемым материалом, воздух поглощает из него влагу и удаляется из камеры. Иногда этот воздух дополнительно подогревают или все тепло, необходимое для сушки, іподводят в сушильную камеру через калорифер.

Сушилка оборудуется тяговыми устройствами для подачи и отвода сушильного агента, устройствами для загрузки и выгрузки высушивае­мого материала, пылеуловителями и др.

На рис. 457 показана основная схема сушильного процесса, характеризуемая однократным использованием сушиль­ного агента. На практике применяют различные варианты сушки и со­ответственно разные аппараты для искусственной сушки.

Обычно расчет сушилок ведут, исходя из количества влажного ма­териала и его начальной и конечной влажности. Для определения коли­чества удаляемой влаги, количества сухого материала, получаемого в результате сушки, а также требующегося расхода тепла и воздуха со­ставляют материальный и тепловой балансы.

Материальный баланс воздушной сушилки. Примем обозначения: —количество влажного материала, поступающего в сушилку, в кгс/час. G2—количество высушенного материала, выходящего из сушилки, е Кгс/час\

Gc—количество абсолютно сухого вещества во влажном материале р Кгс/час;

Wx—влажность материала до сушки в %; W2—влажность материала после сушки в %;

W—количество влаги, удаляемой из материала в сушилке, в кгс/час;

L—количество абсолютно сухого воздуха, проходящего через сушилку, в кгс/час;

Х0—влагосодержание воздуха при входе в калорифер в кгс/кгс сухого воздуха;

Хх—влагосодержание воздуха при входе в сушилку в кгс/кгс сухого воздуха;

Хг—влагосодержание воздуха при выходе из сушилки в кгс/кгс сухого воздуха.

При отсутствии потерь материала количество абсолютно сухого ве­щества в нем до и после сушки остается неизменным. Вес абсолютно сухого вещества, проходящего через сушилку в кгс/час, можно выразить равенством

Г - Г 1 М-Г 100 ~W*

Юо 2 100

Откуда

Г _ r 100 — V^2 А1 —аМ00— UP,

R __ г 100 —

100 — Wo

Количество влаги, удаляемой при сушке, равно разности весов влаж­ного и сухого материала \

W = Gl — G2 ( ^ ' (3—332)

Подставив в последнее уравнение значение G, из уравнения (3—331). получим

W/ г г 100-Wx

1 1 100-U7,

Или

V/ (3-332а)

Подставив в уравнение (3—332) вместо Gj его значение из уравнения (3—331), получим

Ш-Г 100 ~W* П W ~~ 100 — ~~ -

W=.G2 кгс/час I ( (3—3326)

Расход воздуха. При отсутствии потерь количество абсолютно су­хого воздуха, проходящего через сушилку, так же как и количество аб солютно сухого материала, остается неизменным.

При установившемся состоянии процесса в сушилку поступает влаги (в кгс/час):

„ Wx

С высушиваемым материалом................... иг J-Qq

С воздухом........................................ . ... Lx:

Wi

Всего........................ G400

За это же время из сушилки удаляется влаги (в кгс/час):

W2

С высушенным материалом ..... .G8 Jqq

TOC \o "1-3" \h \z С воздухом.................................................... Lx2

~~ ~ W2

Всего. . . G2 J-Qq -J- Lx2

При отсутствии потерь общее количество влаги остается постоян­ным и, следовательно, должно соблюдаться равенство

Gi Ш + Lx, = G2^ + ^ (А)

Количество влаги, удаляемой из высушенного материала в су­шилке, определяется по предыдущему равенством

= V

W 1ПП 2 inn

100 100 Сопоставив уравнения (А) и (Б), получим

W — L(X2 — хг) ■откуда общий расход воздуха на сушку:

W

L =------------ кгс/час (3—333)

X<I Xj

А удельный расход воздуха, т. е. расход его на 1 кгс влаги, удаляемой из материала в сушилке

/ = ~ =---------- ---- кгс/кгс влаги (3—334)

IV #2 " ^Л.

Так как воздух, проходя через калорифер, не поглощает и не от­дает влаги, то его влагосодержание при нагревании в калорифере остается неизменным и, следовательно

Л-1 = х0

Откуда

1 кгс/кгс влаги (3—334а)

Х2 — хО

Тепловой баланс воздушной сушилки. Примем обозначения: Q—полный расход тепла в сушилке в ккал/час\ QK—расход тепла в калорифере в ккал/час-,

<2Д—добавочное тепло, вводимое непосредственно в сушильную ка­меру, в ккал/час-,

Q

= W—общий удельный расход тепла в сушилке в ккал на 1 кгс влаги; _QK

<FK — щ—удельный расход тепла в калорифере в ккал на 1 кгс влаги;

Я я — If—удельный расход добавочного тепла в сушильной камере в

Ккал на 1 кгс влаги; /0, t0—теплосодержание в ккал/кгс и температура воздуха перед

Калорифером в °С; /г, іЛ—то же после калорифера; /2, t2—то же после сушилки;

/0—теплосодержание водяного пара при /0 в ккал/кгс; ix—теплосодержание водяного пара при tx в ккал/кгс; /2—теплосодержание водяного пара при t в ккал/кгс; 6j—температура материала при входе в сушилку в °С; 62—температура материала при выходе из сушилки в °С; см—теплоемкость высушенного материала в ккал/кгс °С сс—теплоемкость абсолютно сухого материала в ккал/кгс °С; GT—вес транспортных приспособлений в сушилке в кгс/час; с. г—теплоемкость материала транспортных приспособлений в ккал/кгс• °С.

Х.—температура транспортных приспособлений при входе в су­шилку в °С;

/т. вых.—температура транспортных приспособлений при выходе из сушилки в °С;

Qn—потери тепла сушилкой в окружающую среду в ккал/час\

П 1

Яп — ^—потери тепла, отнесенные к 1 кгс влаги, удаляемой из материала в сушилке.

Для установившегося состояния процесса тепловой баланс воздуш­ной сушилки может быть составлен по данным, приведенным в табл. 23.

Баланс тепла в воздушной сушилке

Приход тепла в ккал/час

С воздухом. . .

С влагой материала"

С материалом. .

С транспортными приспо соблениями

От источника тепла в кало рифере

От источника тепла в су шильной камере....

С отходящим воздухом. . LIt

С сухим материалом. . . GjCM6,

С транспортными приспо­соблениями GTCT<T. вых.

Потери в окружающую среду Qn

Всего L/a-f-GacM024-

Всего L/o+lFei+GaC. A-}-

Вх. +qk+qn

Приход тепла должен быть равен расходу, т. е. должно соблю­даться равенство

£/.+ W6, + G2CA + GTcJT вх. +<2к + <2д == ЬІг + G2cA 4- GTcА вых. + Q»
Или

Q — QK + Qa — L(I2 — /0) + G2Cm(62-Вг) + GTcT (TT. Вых.вх.) + Qn-

Деля обе части последнего уравнения на W, получим удельный >д тепла: ^

= Я = 9к + дД = [6] (H — Ям + + Яп — ві (3—335)

Где

= (3—336)

Q ________________________________ GTcT (Tr, ВЬ1Х. вх.) ^__ 337)

U?

Удельный расход тепла в калорифере определяется из уравнения (3—335)

QK = / (/а - /0)1+ </м + + <7п - <7Д (3-338)

Удельный расход добавочного тепла в сушильной камере

<7д = / (/, ■- /0) + <7м + Яг + <7п - - <7к (3-339)

Подставив в уравнение (3і—335) значение / из формулы (3—334а). получим следующее выражение для удельного расхода тепла:

Я = Я, + Я, = -^Г + 9м + + ^п - Єї (3-340)

Где -

Zq^qu + qr + qft (3-342)

Теоретическая сушилка. Для исследования процессов сушки рас­смотрим так называемую «теоретическую сушилку», в которой тепло, до­бавочно сообщенное в сушильной камере, полностью компенсирует потери тепла в окружающую среду, на нагрев транспортных приспособле­ний и сухого материала.

Для такой теоретической сушилки

<7д + = <7м + Ят + <7п и уравнение (3—335) принимает такой вид

Q = QK = L (/2 — /0) Ккалікгс Влаги (3—343)

Удельный расход тепла в калорифере можно выразить равенством

QK — l (/І—/0) ккалікгс влаги и, следовательно, в теоретической сушилке

/</,-/о) «/</.-/*)
Откуда

'(Л —/і) = 0

Или

/, = /2=const

Полученное равенство показывает, что втеоретической су­шилке теплосодержание воздуха при протека­нии его через сушильную камеру остается не­изменным, т. е. воздух меняет в сушилке свое состояние при /=const. Если сушку ведут предварительно по­догретым воздухом, т<эиспарение влаги происходит только вследствие охлаждения воздуха; при этом влага вносит в воздух ровно столько же тепла, сколько он отдает, охлаждаясь, на испарение влаги.

Подставим в уравнение (3—343) значения теплосодержания воздуха

/2 = 0,24га + х2/2; /0 = 0,24*0 + x0i0

Тогда

Я = 0.24/ (/2 — g +1 (x2i2 — xj0)

Если к выражению в скобках во втором члене уравнения прибавить и вычесть из него x0i2, получим

Q = 0,24/ (/2 — /0) + / (х2 — *0) іг / (і2 - /0) х0

Но согласно уравнению (3—334а)

/ (х2 — х0) = 1

Я

I (і2 — і0) х0 = lx0 (0,46/2 - I - 595 — 0,46/о — 595) = 1х0 0,46 (/2 — /в) Следовательно

Q =1 (0,24 + 0,46х0) (/2 - /0) 4- H (3—344)

Полученное уравнение дает наглядное представление о структуре теплового баланса сушилки и показывает, что в теоретической сушилке тепло расходуется:

на испарение влаги

І2 Ккал/кгс влаги

Тна потери с отходящим воздухом

/ (0,24^4- 0,46х0) (/2J— /0) ккал/кгс влаги

Причем расход тепла будет тем меньше:

А) чем ниже температура отходящего воздуха и выше температура воздуха, поступающего в калорифер, и

Б) чем меньше удельный расход воздуха.