АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Расчеты процесса экстрагирования твердых тел
Треугольная диаграмма тройных смесей. При экстрагировании твердых веществ в экстрактор поступают: 1) исходная смесь твердых веществ F, Содержащая извлекаемый из нее растворимый компонент В и нерастворимый или инертный компонент А; 2) жидкий растворитель 5, представляющий собой либо чистый компонент С, либо смесь нескольких взаимно растворимых веществ.
В целях упрощения будем считать, что в данном случае имеется система, состоящая из трех компонентов и двух фаз. Одна фаза жидкая, представляет собой верхний поток, или экстракт, состоящий из растворителя С и растворенного в нем компонента В. Другая фаза представляет собой и и ж - ний поток, или р а ф и н а т, состоящий из нерастворимого инертного компонента А и частично удержанной им жидкости—раствора компонента В в растворителе.
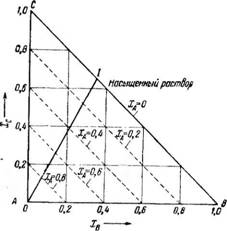
Данная трехкомпонентная система может быть представлена графически на треугольной диаграмме (рис. 408). Наносим на диаграмму равнобедренный прямоугольный треугольник, на горизонтальной стороне его в определенном масштабе в весовых долях от Одо 1,0 откладываем содержание растворимого компонента В, а на вертикальной стороне—содержание растворителя—компонента С. Точки, лежащие на гипотенузе треугольника, будут соответствовать содержанию компонента А.
Будем выражать содержание компонентов в смеси в весовых долях и примем следующие обозначения: Ха—содержание компонента А; хв—содержание компонента В; хс—содержание растворителя С;
Для любой точки, находящейся внутри треугольника, имеют место равенства:
ХА + хв + хс = 1 (3—232)
|
Рис. 408. Диаграмма тройной системы при экстрагировании из смеси твердых веществ (А 4- В) растворимого компонента В с помощью жидкого растворителя С. |
КА = 1 — Хв—Хс (3—233)
Из уравнения (3—233) следует, что величина хА не является самостоятельной, а полностью определяется заданными значениями Хв и xq. Начало диаграммы (хв =0 и Хс =0) соответствует содержанию только инертного компонента А. Линии, параллельные гипотенузе треугольника, являются линиями постоянного содержания инертного компонента (Ха —К), так как уравнения этих линий
Хс = —хв + D (3—234)
Xc + xB=D (3—235)
Где D—константа.
Из уравнений (3—233) и^(3—235) следует, что
ХА = 1 — д:с — Хв= 1 — D = К (3—236)
При данной температуре насыщенный раствор компонента В в растворителе представляется на диаграмме точкой /, лежащей на гипотенузе треугольника. Область на диаграмме выше линии, соединяющей эту точку с началом координат, представляет часть диаграммы, соответствующую
|
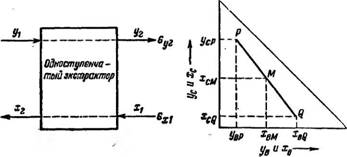
Рис. 409. Материальный баланс одноступенчатой экстракции твердых тел. |
Собственно экстрагированию, т. е. переходу компонента В из твердой фазы в жидкую. В этой области нерастворенного компонента В нет. Область, лежащая ниже линии, соединяющей точку / с началом координат, соответствует твердой фазе, содержащей компоненты А и В и задержанный твердой фазой раствор с концентрацией, соответствующей концентрации жидкости в точке /.
Одноступенчатое экстрагирование. Рассмотрим установившийся процесс одноступенчатого экстрагирования (рис. 409).
Обозначим:
Gyi—весовой расход верхнего потока при входе в систему в кгс/час;
Gyi—весовой расход верхнего потока при выходе из системы в кгсIчас];
GX1—весовой? расход нижнего потока при входе в систему в кгс/час;
GX2—весовой расход нижнего потока при выходе из системы в кгс/час; у—содержание компонентов в верхнем потоке в вес. долях; х—содержание компонентов в нижнем потоке в вес. долях.
Содержания компонентов у и х не будут откладываться на разных осях диаграммы; такие обозначения приняты лишь для того, чтобы указать, к какому потоку относится содержание компонентов. Индексы А, В, С, стоящие при х и у, указывают, концентрации какого компонента выражают х и у, а индексы 1 и 2—соответственно концентрации этих компонентов при входе в систему (1) и при выходе из нее (2).
Общий материальный баланс для всей системы выражается уравнением
GX1 + Gyi == Gxz + Gy2 (3—237)
Материальный баланс компонентов В и С соответственно имеет такой
Вид:
GXlxB\ + GYiyBI = GX2XВ2 -b СУгу в2 (3—238)
GXxXC\ + GYiYCI — GX2XC2 - f GMYa (3—239)
Материальный баланс можно представить и в более общем виде. Для любого момента экстрагирования можно считать, что верхний поток имеет весовой расход Gy, нижний поток—Gx\ состав верхнего потока—У И нижнего—х. В результате смешения обоих потоков образуется смесь в количестве GM С составом хм.
Уравнение материального баланса в этом случае может быть представлено выражениями:
GM = GX + Gy (3-240)
GMXm = Gxx + Gyy '= (Gx + Gy) XM (3—241)
Из этих двух уравнений следует, что отношение между весовыми количествами потоков выражается уравнением прямой
(3-242)
ХМ ~~ У І
Представленной на диаграмме рис. 409. Из диаграммы видно, что от-
РМ
Ношение между весовыми количествами потоков равно отношению - Щ-
Между длинами отрезков РМ. и MQ.
Рассмотренный метод графического изображения потоков позволяет найти зависимость между весовыми отношениями потоков и концентрациями их при входе в систему и при выходе из нее.
По уравнению (3—241) для компонентов В и С можно написать:
GMXBM = Gx1Xbi + GyiyBi — (GX1 + Gyi) X Вм\ (3—243)
GMXcm = GXlxCi + GYiYC\ = (GX1 + Gyi) ХСм (3—244)
Откуда следует, что
|
|
|
(3—245) |
|
XI |
СВМ *В1 ХСМ ХС1
Уві ХВ м Ус\ XCi G
|
|
Иллюстрацией к этому уравнению служит диаграмма рис. 410. Допустим, что твердый материал (нижний поток) поступает на экстрагирование в виде смеси компонентов А и В с содержанием компонента В, равным Хв1=0,20 вес. дол.
Так как смесь растворителя 5 в своем составе компонента В не имеет, точка Хві лежит на горизонтальной оси. Если растворитель (верхний поток) представляет собой чистый компонент С, то точка уві должна лежать на вершине треугольника.
Из сопоставления уравнений (3—243), (3—244) и (3—245) следует, что состав смеси хм должен характеризоваться точкой, лежащей на линии, соединяющей точки Хві и уві. Положение этой точки определяется весовым отношением потоков. Из этих уравнений следует, что точка Хм должна
Лежать на линии, проходящей через точки уВ2 и хВг, причем в практических расчетах ни та, ни другая концентрация не бывают заданными. Местоположение точек ув2 и Хв2 определяется следующим образом.
В предельном случае можно принять, что компонент В полностью растворен и в составе твердой фазы его нет. Этому соответствует условие, что хв = 0 и Хс = 0. Такое состояние характеризуется точкой, лежащей в начале диаграммы. В то же время эта точка должна лежать на одной прямой с точками Уві и хВ\ . Проводя из начала осей прямую через точку хм до пересечения с гипотенузой треугольника, получаем точку Уві • Точка хВ2 должна также лежать на прямой, проходящей через точки */В2 и Хм и начало осей координат. Местоположение этой точки определяется отношением между весовыми количествами раствора, находящегося в твердой фазе, и твердым компонентом в нем. Допустим, что это отношение равно 1,5, т. е. допустим, что в твердой фазе после экстракции на 1 кгс твердого компонента задерживается 1,5 Кгс раствора. Этому условию на диаграмме (рис. 410) отвечает линия, параллельная гипотенузе треугольника, отсекающая на осях диаграммы отрезки Хс = 0,6 и л'в = 0,6. Точка Хв2 должна лежать на пересечении этой линии с линией, проходящей через точки ув2 и хм и начало координат.
Таким образом, состав верхнего слоя уж и состав нижнего слоя ХВ2 на выходе из системы "определяются отношениями количеств растворителя и твердого экстрагируемого материала и отношением между количеством жидкой и твердой фазы в твердом веществе после экстрагирования. Практически, пользуясь треугольной диаграммой, либо принимают заданными указанные весовые отношения и находят по диаграмме концентрации уВ2 и xpj2, либо по заданным концентрациям г/вг и хР2 находят необходимые указанные весовые отношения.
Многоступенчатое противоточное экстрагирование. На рис. 411 представлена схема многоступенчатого (п ступеней) противоточного экстрагирования. Смесь твердых веществ, подвергающаяся экстрагированию, поступает в первую ступень установки в количестве Gxo Кгс/час с содержанием компонента В, равным х0 вес. долей. С другого конца установки в последнюю ступень вводится растворитель в количестве Gy(„+i) Кгс/час, имеющий концентрацию. У{П+\).
Обший материальный баланс для всей установки выражается уравнением
GXo -+- Gy{N+1) — Gxn -Ъ Gyi (3—246)
А материальный баланс компонента В уравнением
GXox0 + Gy <п+1) Уп+1 = Gxnxn + Gyiy1 (3—247)
|
О, г |
|
А о,1 Xet=O,2 Доля (Вес J Компонента В |
|
Рис. 410. Диаграмма одноступенчатого экстрагирования |
|
1,0 | I 0,§ І |
|
І |
По-предыдущему наносим на горизонтальную ось треугольной диаграммы (рис. 411) точку х0, соединяем эту точку С ТОЧКОЙ Уп+L (на практике состав твердой фазы х0 и состав растворителя Yn+I, поступаю-
Тих на экстрагирование, Gy(N+1)
Отношении, равном
JxО
Известны) и, разделив полученную прямую в получаем на этой прямой^точку, отвечающую
Хсм—содержанию компонента в смеси.
Зная отношение между весовыми количествами жидкой и твердой фаз в нижнем потоке (т. е. в рафинате) при выходе из установки, наносим на диаграмме линию постоянного состава твердой! фазы, параллельную гипотенузе треугольника, и
Отмечаем на ней точку хп. соответствующую содержанию растворимого компонента В в твердой фазе, выходящей из установки. Согласно уравнениям (3—246) и (3—247) точки хп, хсм и уЛ должны лежать на одной прямой. Отсюда находим местоположение точки ух как точку пересечения линии, проходящей через точки хп и хсм. с гипотенузой треугольника. Таким образом, все предельные, начальные и конечные концентрации системы нанесены на диаграмму.
|
G |
|
Хт |
|
= Grmx, |
|
Gv„— G, |
|
(3—250) (3—251) |
Напишем уравнение материального баланса для части системы в пределах от первой ступени ДО ступени /77 ВКЛЮ - Чительно:
G,
ХтГт
Gy (т+\)Ут+\
(3—249)
M Обозначим R
И
RXr = GX0XQ — Gyiyx Тогда уравнения (3—248) (3—249) принимают вид:
R = GXo Gyi = СХЛ — Gm = • • • Gxn — Gy (Я+-1
|
Лу(гм} |
|
|
|
-Gy(M +1) (3—248) |
|
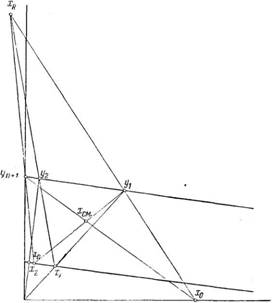
Рис. 411. Графическое определение числа ступеней многоступенчатого противоточного экстрагирования из смеси веществ. |
RXR — GXox0 — Gyiyl = GXlxx — Gy2Yz = Gxnxn — Gy (/г+І)уп+1
|
|
Из этих уравнений следует, что точка xR определяется пересечением прямой, проходящей через точки х0 и ylt с прямой, проходящей через хп и Уп+I, так как точка хр должна лежать на обеих этих прямых.
Графическое решение задачи теперь может быть проведено как с начала, так и с конца системы. Если начать с первой ступени, то положение точки уу уже известно, и можно, соединив эту точку с началом диаграммы на линии постоянного состава твердой фазы, найти точку пересечения хЛ. Из уравнения (3—250) и (3—251), имея в виду, что
R = GX,— Gy2
И
RxR = СХххЛ — Gyzy2
Находим точку у2 как точку пересечения линии, проходящей через точки ^ и с гипотенузой треугольника. Такие построения проводим до тех пор, пока не получим точку х, соответствующую составу, равному или меньшему заданного состава хп. Число полученных при этом линий, соединяющих начало осей координат с точками х1г х2, ■ - - хп, и будет соответствовать теоретическому числу ступеней экстрагирования, необходимых для проведения противоточного многоступенчатого экстрагирования при заданных условиях.
Материальные потоки и объем экстракторов. Практически при расчете экстракционных установок задано:
GXo'—вес исходной смеси твердых веществ, подвергающейся экстрагированию, в кгс/час',
Хв0—содержание в исходной смеси извлекаемого из нее растворимого компонента В в вес. долях; а—степень извлечения компонента В из смеси в %;
Г/в0—содержание компонента В в исходном растворителе в вес. долях;
*/Во—содержание компонента В в растворе после экстрагирования в вес. долях;
Р—количество раствора, задерживающегося в твердой фазе (в рафй - нате) после экстрагирования, в кгс на 1 кгс компонента А. Эта величина может быть выражена следующем образом:
ХАп
П = у^тр (3—253)
Пользуясь принятыми выше обозначениями, определяем (в кгс/час)',
Количество компонента В, извлекаемого из исходной смеси в результате экстрагирования
GB3 = G,0*bo~ (3-254)
Количество раствора (экстракта), получающегося в результате экстрагирования
Gyn=~ (3-255)
J Увп І
Количество растворителя в растворе
Gci=Gyn(l—yBn) (3-256 )
Количество компонента В в твердой фазе (в рафинате)
GBR = (і — щ):0с0хво (3-257)
Количество компонента А, остающегося в твердой фазе после экстрагирования
G, A = G, O(1-;xbo) (3-258)
Общее количество твердых веществ в рафинате после экстрагирования
GT. n. — Gx0 (1 — *во) + (1 - fig) GXoxво (3-259)
Количество растворителя, уходящего с твердым материалом после экстрагирования
Gc2 =Gx,( 1—*во)Р (3-260)
Содержание инертного компонента А в рафинате после экстрагирования
1
Ха п
Общий расход растворителя
Gy = Gci + Gc2
|
(3—261) (3—262) |
Отношение веса растворителя к весу исходной смеси, поступаю щей на экстрагирование
|
|
|
Gci + G< |
|
C2 |
(3—263)
|
|
При работе в одном аппарате в одну ступень объем экстрактора определяется равенством:
|
|
Gx0 (1 — *Вр)
|
GXox |
|
Во |
|
(3—264) |
|
V = |
|
+ |
|
+ |
|
3600-fj |
|
Ув |
|
Тс |
ЇА
|
|
Где та—удельный вес твердого компонента А в кгс/м3; Тв—удельный вес компонента В в кгс/м3; Тс—удельный вес растворителя в кгс/м3; ч]—степень заполнения аппарата; обычно принимают tj=0,7; т—продолжительность насыщения раствора компонентом В до заданной концентрации в сек. При работе в одном аппарате и многократном заполнении его растворителем объем экстрактора можно определить следующим образом:
При первом заполнении экстрактора в него может быть залито растворителя
|
|
Gx0XBO GXo (1 —
Gyi —
Їв ЇА
|
ЗбООуг |
|
V-N |
При последнем заполнении может быть залито растворителя
|
|
|
Gxo*BO ' 1 |
|
3600ус |
|
100 |
|
V4 |
|
Gyn = |
|
Yb |
Gx о (1 — хво) Та
|
|
Среднии расход растворителя при каждом заполнении определяется как
|
|
|
Gv |
|
Ср. |
__ Gy і + Gy п
|
|
ИЛИ
|
|
|
Gxо 100 |
|
3600ус |
|
Gy ср. =}УГ1 — |
Gx0X во Gxо (1 — хт)
|
2їт |
|
YA |
+ "
Yb
|
|
Или
|
|
|
\Уг( — С] |
3600уг
Gy ср. —
Yb YA ■'YB
При заданном объеме экстрактора число заполнений его растворителем определяется как
С,
Или
П^ 3600^---------------------------------------------------- (3-266)
—Г-(^-С)
При заданном числе заполнений объем аппарата определяется как
Gyx 3600успС
17 = 3600успт] ~ Ж (3-267)
В противоточной многоступенчатой установке через все экстракторы, в единицу времени протекает одно и то же количество растворителя. В этом случае независимо от числа ступеней объем каждого аппарата можно принять
У = + ^ + С*о(1-Хво) (3—268)
3600ус Yb Ya
Расчет экстракционных аппаратов затрудняется из-за отсутствия данных для определения скорости экстрагирования или скорости перехода растворимого твердого компонента В из твердой фазы в жидкую фазу. Эти данные могут быть получены только при проведении серьезных научно- исследовательских работ. В настоящее время скорость экстрагирования из твердых веществ для каждого частного случая приходится определять опытным путем.