АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Гидродинамика зернистых материалов
В химической промышленности широко распространены процессы взаимодействия газов и жидкостей с зернистыми твердыми материалами. В зависимости от скорости потока газа или жидкости возможны следующие случаи:
1) газ или жидкость при небольшой скорости потока проходят сквозь слой зернистого материала, как через фильтр. При этом частицы или зерна твердого материала, образующего слой, находятся в состоянии покоя и перепад давления или сопротивление слоя по мере увеличения скорости потока соответственно увеличивается;
2) слой зернистого материала при достижении определенной скорости потока начинает заметно увеличиваться в объеме, отдельные частицы его приобретают способность перемещаться и перемешиваться, а перепад давления становится постоянным;
3) частицы материала слоя при дальнейшем увеличении скорости потока газа или жидкости увлекаются потоком и образуют взвесь. Это состояние наступает тогда, когда сопротивление движению отдельной частицы, взвешенной в газе или жидкости, становится равным весу частицы в данной жидкой или газообразной среде. Такое состояние слоя зернистого материала называют псевдоожиженным, а слой кипящим. Скорость частиц твердого материала, взвешенных в газовом или жидкостном потоке, называют скоростью витания
^ВИТ. »
4) при увеличении скорости потока до величины, большей скорости витания, т. е. при w > шВИт, твердые частицы выносятся потоком газа из аппарата, как это происходит при пневмотранспорте;
5) если скорость потока меньше скорости витания, т. е. при w < шШ1Т>, вавешенные в газе или жидкости твердые частицы под влиянием силы тяжести осаждаются.
Сопротивление слоя зернистого материала. Перепад давления в слое зернистого материала можно, пользуясь общими положениями гидродинамики, выразить уравнением
АР = С-^ (А)
Где у0 — удельный вес газа или жидкости в кгс1мг\
W0 — скорость газа или жидкости в каналах слоя зернистого материала в м! сек;
I
1.— коэффициент сопротивления, С, = (X—коэффициент трения;
/ — высота слоя материала в ж; с1э—эквивалентный диаметр каналов в м).
В общем случае коэффициент трения X может быть выражен в виде функции от критерия Рейнольдса:
Основным при определении перепада давления или сопротивления слоя зернистого материала является установление этой функциональной зависимости. На основании проведенных нами работ[6] этот вопрос решается следующим образом.
Допустим, что слой зернистого материала объемом V—1 м3 состоит из п частиц, имеющих форму шара диаметром d.
Объем собственно частиц в слое составляет
Т, Tzds
Уо= — п а1 их общая смоченная поверхность
|
V^^V-Vo |
?сы. = -*d2n = - gj П
Свободный объем пор или каналов в слое а пористость слоя
V-v0
При V=l м3
E=l-V0
У0=1-в
Эквивалентный диаметр каналов
D
"экв. ------ р
|
Тid3n |
І сы.
ИЛИ
TOC \o "1-3" \h \z / ,тid3 \ 2
4 I 1 - --- g-- nl "jj" dt
Экв' бгаі3 1 — є
~6d~n
А для зерен любой формы с диаметром d3
D
"•ЭКВ. I ___ є
Где Ф— коэффициент, учитывающий зависимость эквивалентного диа-
О
Метра частиц от их формы; для частиц шаровой формы Ф= —.
Если w — скорость газа или жидкости, отнесенная ко-всему сечению слоя зернистого материала, то скорость газа или жидкости в каналах слоя может быть выражена равенством
W
= —
Критерий Рейнольдса для данного случая определяется равенством:
_ ЩАжа. Ъ _ «!!_ То
Є 1 £
Или
Ф
Re = Re,
1 — £
R JVdsU 3 fig -
Имея в виду, что в общем случае коэффициент трения может быть выражен равенством
При подстановке найденных значений X, w0 и d3KB. в уравнение (А) получим:
|
(1-9D |
Др _ А I а^о (1-є)2 І
Re3 d3 2g фа
Или
Где
6 А. Г. Касаткин.
®ф —коэффициент формы, зависящий от размеров и формы частиц
Слоя. Этот коэффициент показывает, во сколько раз площадь смоченной поверхности слоя, состоящего из данных частиц, больше площади смоченной поверхности слоя, состоящего из шарообразных частиц при ci3 = d. Этот коэффициент можно найти только опытным путем. Опытным путем найдено, что при значениях /fe<35
<'-92)
А при значениях 70 < Re3 < 7000
YRe3
Область 35 < Re3 < 70 является переходящей.
Подставляя найденные значения коэффициента трения из последних двух уравнений в выражение потерянного напора (1—91), найдем следующие выражения для коэффициента формы: при Re3 < 35
?ф= 0,0091 7Т^Г7 Ей • Re3 (1-93)
При 70 < Re3 < 7000
СрФ =0,173 „ Ей Re3 (1 —93а)
Где
Ей-.
Таким образом, при инженерных расчетах гидравлического сопротивления слоя зернистого материала необходимо по данным одного опыта, при любой скорости потока и температуре, для зерен данного гранулометрического состава d3 , найти по уравнениям (1—93) и (1—93а) коэффициент формы <рф. Зная последний, можно рассчитать сопротивление слоя данного материала при любых условиях по уравнению (1—91).
Скорость витания тъит.. В момент перехода слоя зернистого материала в состояние псевдоожижения перепад давления достигает такой величины, при которой общее давление на слой материала становится равным весу материала. В этих условиях
Л PfW0(T-T0)
Или
APF = Fl{\ є) (ї То)
Где F—общая поверхность поперечного сечения слоя в л*2;
У — удельный вес частиц твердого материала слоя в кгс! мъ\ Подставляя в последнее уравнение значение ДР из уравнения (1—91), находим
«4пг. Т. (l_^cpoF = jF/(1_e)(T_To)
3 d3 2 g
Откуда
2g4 (Y — Yo) Ј8 *s<P®Yo (1 — Ј)
Или, умножая числитель и знаменатель правой части на d23 и v2, получаем
V2 W^oU —О
Где v—кинематическая вязкость газа в м2/сек.
В последнем уравнении левая часть представляет собой в критериальной форме
2 ®BHT. d3
Rei =
V-
4 а отношение
Gd3 (у — Yp)
Представляет собой безразмерный критерий Архимеда, учитывающий
Влияние ускорения подъемной силы (множитель ^ ~ 8 місек2).
Yo
Критерий Архимеда
V 10
Состоит из величин, которые не зависят от скорости и режима потока, и поэтому числовые значения его могут быть найдены, если только известны размеры частиц, их плотность, а также плотность газа или жидкости и их вязкость при заданных условиях процесса.
В критериальной форме уравнение (1—936) принимает вид:
П 2 2е3Аг Неъ
Мі — є) Уф
Или
Re2 W^L (1—95)
Где
Ф=тт—Ч— (1—96)
Т О — £) <Рф
Подставляя в уравнение (1—95) значения Х3 из уравнений (1—92) и (1—92а), для условий псевдоожижения получаем:
При tff?3<35 или при tyAr < 3,85-103
/&?3 = 0,0091фЛ/- (1—97)
При 70 < Re3 < 7000 или при 9,86-10* < $ Аг < 31,14 106
Re3 = 0,367 (фЛг)0*57 (1—98)
Зная значение критерия Рейнольдса, можно найти величину скорости псевдоожижения из равенства
= (>-99)
Когда скорость w потока газа или жидкости равна скорости витания aw. ,Т0 твердые частицы находятся во взвешенном состоянии и их относительная скорость движения равна нулю. Если скорость потока больше скорости витания находящихся в нем твердых частиц, частицы будут уно-
|
(1—936) |
6*
ситься потоком. Если же скорость потока меньше скорости витания, т. е. если Довит. > w, то твердые, взвешенные в потоке частицы будут падать вниз и осаждаться со скоростью w0 — wBHT. — w.
Скорость осаждения. Скорость падения тел в безвоздушном пространстве определяется по известной формуле
W = gx мі сек
Где g — ускорение силы тяжести в м/сек2--
Т— время падения в сек.
По этой формуле можно достаточно точно определить и скорость падения тел большего размера в воздушной (газовой или жидкой) среде, так как сопротивление среды при этом незначительно и уменьшает силу тяжести всего на 0,05—0,1%.
Однако при падении тел очень малой величины, например частиц размером 100 мк и менее, сопротивление среды настолько увеличивается, что эти частицы через сравнительно короткий промежуток времени после начала падения начинают двигаться с некоторой постоянной скоростью, которая является их конечной скоростью падения. Таким образом, движение частиц вследствие того, что силы сопротивления среды уравновешивают силу тяжести, переходит из равномерно ускоренного в равномерное. Скорость такого равномерного падения частиц в газообразной или жидкой среде будем называть скоростью осаждения и обозначать ее w0 м/сек. Эта скорость может быть определена из общего закона сопротивления движению тела в среде.
Сила сопротивления среды в общем случае определяется по закону Ньютона
5 = CFr0^ кгс (1—100)
И для частиц шарообразной формы
S = кгс (1—100а)
Г? та^2
Где г — ----------- проекция поперечного сечения частицы на направление ее
Движения в м2.
Сила тяжести частицы в газообразной или жидкой среде:
С = (ї — То) кгс
При достижении частицей постоянной скорости—скорости осаждения—сила сопротивления уравновешивает силу тяжести и должно иметь место равенство:
„ 7id2 Yo^o __ 7id2 . .
^ ~4 2G~ ~~ 6 'т То'
Откуда
П^уіШЕШ <1—Ю1>
Коэффициент сопротивления С является функцией критерия Рейнольдса и определяется опытным путем в зависимости от скорости движения частиц, плотности и вязкости среды.
Экспериментально установлено, что коэффициент сопротивления имеет следующие значения: при Re < 2
При 2<Яе<500
(1—103)
А при 500 < Re < 150 000 величина коэффициента сопротивления становится постоянной и равной С = 0,44.
|
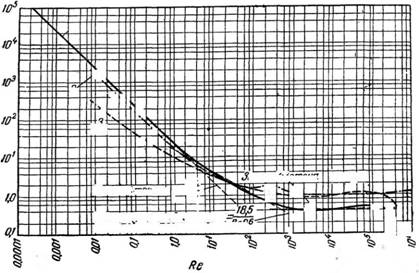
Рис. 28. Зависимость коэффициента сопротивления от числа Рейнольдса. |
Зависимость между коэффициентом сопротивления С и критерием Рейнольдса, полученная на основании многочисленных опытных данных, представлена на рис. 28.
Подставив значение С при Re < 2 в уравнение (1—101), получим
Ш0 = d2(J~Vo) м/сек (1-104)
И lop.
Уравнение (1—104) является следствием закона Стокса, по которому величина сопротивления среды при осаждении в ней мелких взвешенных частиц определяется из выражения
S = Зігб/|ійУ0 (1—105)
При S=G
Izd?
3 Izd\i. w0 — —G— (ї — To)
И, следовательно,
DH-ї-Го)
18fx
Математическое выражение закона Стокса можно также получить путем подстановки в уравнение (1—100а) значения С из уравнения (102).
По закону Стокса, как это видно из уравнения (1—105), сила сопротивления среды при падении в ней мелких
Взвешенных частиц пропорциональна скорости падения в первой степени.
Этот закон имеет сравнительно узкие границы применения. Верхним пределом применения его является, как указано выше, условие ^е<2. Максимальный размер частиц, осаждение которых происходит по закону Стокса, определяется подстановкой в уравнение (1—104) вместо скорости-
Осаждения wQ ее значения из критерия Рейнольдса, т. е. w = • При
Re—2 имеем
DMaKc =у з ^ м (1__106)
Макс у (Y_Yo)Yo ' Г (Y—То) То V
Нижним пределом применения закона Стокса являются условия осаждения, при которых размеры взвешенных частиц достигают величины, равной среднему пробегу молекул среды /0 со взвешенными частицами. В этом случае закон сопротивления принимает форму
Зтіфш0 ^___ jq^
In
Где /0= 107 — средний свободный пробег молекул газа при данных условиях; А—константа (Л= 14—20).
Скорость осаждения в этом случае определяется уравнением
С-108)
При значениях критерия Рейнольдса 500</?е< 150 ООО величина коэффициента сопротивления С=0,44. Подставив это значение в уравнение (1—101), получим для данного режима скорость осаждения
W0 = 5,48і/"——— м/сек (1—109)
" Yo
Таким же образом можно было бы найти скорость осаждения и для промежуточной области, подставляя в уравнение (1 —101) значения из уравнения (1 —103).
Для определения скорости осаждения по уравнениям (1—101), (1—104) и (1—108) необходимо предварительно знать значение критерия Рейнольдса, в который входит и искомая скорость осаждения. Поэтому приходится заранее задаваться либо величиной wQ, либо Re и в дальнейшем проверять скорость осаждения по указанным уравнениям, что практически неудобно.
Для того чтобы избежать этого, целесообразно пользоваться следующим методом определения скорости осаждения.
Из уравнения (1—101) имеем
0 Зу0
Подставляя вместо скорости осаждения ее значение из критерия Рейнольдса w0 = , получим ^
ГП 2 4dS(Y-Yo) РоА
Или в критериальной форме согласно (1—94):
4 Аг
CW —з
Откуда
Ar = ~lRe* (1—110)
Последнее уравнение при подстановке в него критических значений критерия Рейнольдса позволяет найти соответствующие критические значения и для критерия Архимеда, в выражение которого скорость осаждения не входит.
Для осаждения в условиях, когда действует закон Стокса (т. е. при Re < 2), С — , а критическое значение критерия Архимеда
Аг = = 18- 2 = 36
Кр.
Для промежуточного режима осаждения (т. е. при 2</?«<500) 18,5
£= ^о^ и критическое значение критерия Архимеда:
, 3 18,5 3-18,5.бОО1-* с, ллл ^кр - = Т -/7ео7б - = 84 000
В условиях автомодельного режима осаждения значение критерия Архимеда больше 84 ООО, т. е. Агкр > 84 ООО.
При использовании значения критерия Архимеда вычисление скорости осаждения в любом режиме сводится к трем операциям:
1. По уравнению (1—94) находим значение критерия Архимеда
J[r = d3g(r — То) v2y о
2. По найденному значению критерия Архимеда устанавливаем режим осаждения и определяем число Рейнольдса:
При Лг<36
П
Ке 3 24*
Или
Re=% (1-111)
При 36<Лг<84 ООО
Re=l±jL)h
|
Или |
* 1 3 18,5/
Или
При Лг>84 ООО
Re=Ут-m
,44
Re=\J\VAr
|
|
Где ср — коэффициент, учитывающий форму взвешенных частиц.
|
3. Находим скорость осаждения по уравнению |
Для частиц шарообразной формы коэффициент 9=1, а для частиц неправильной формы 9<1.По опытным данным, полученным в условиях осаждения при автомодельном режиме, т. е. при Лг<84 ООО, практически можно принять для частиц округлой формы 9 = 0,77, для частиц угловатой формы 9=0,66, для частиц продолговатых 9=0,58 и для пластинчатых частиц 9—0,43.
Для определения скорости осаждения частиц неправильной формы необходимо в выражении критерия Архимеда и формуле скорости осаждения вместо эквивалентного диаметра частиц подставить диаметр, определяемый в общем случае как
|
|
Где G — вес частицы; Т — УД. вес частицы.