АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ

Фазовое равновесие

Фактор интенсивности. Протекание диффузионных процессов обу­словливается наличием в системе двух фаз и заключается в переходе вещества из одной фазы в другую. Процесс перехода вещества из одной

29 А. Г. Касаткин

Фазы в другую, т. е. массообмен, или массопередача, в изо­лированной замкнутой системе, состоящей из двух или большего числа фаз, возникает самопроизвольно и протекает до тех пор, пока меж­ду фазами при данных условиях температуры и давления не уста­новится подвижное фазовое равновесие, при котором в единицу времени из первой фазы во вторую переходит столько же молекул, сколь­ко в первую из второй.

Как известно из термодинамики, любой процесс, самопроизволь­но протекающий в замкнутой изолированной системе, характеризуется фактором интенсивности данного вида энергии. Так, при про­текании гидродинамических процессов фактором интенсивности является высота напора или гидродинамическое давление, а при, протекании тепло­вых процессов фактором интенсивности является температура.

Возникновение самопроизвольного процесса, его направление и предел перехода данного вида энергии из одной части системы в другую зависят только от числового значения фактора интенсивности в разных частях системы, а"в тепловых процессах—от термодинамического по­тенциала.

Процесс возникает самопроизвольно при условии, что числовые значения фактора интенсивности в разных частях системы не равны или если термодинамический потенциал в системе больше нуля. Процесс проте­кает в направлении от части системы с большим фактором интенсивности к части с меньшим фактором интенсивности и, наконец, система приходит в состояние подвижного равновесия, когда все части ее имеют одина­ковый фактор интенсивности и термодирямииргк-ий потенциал системы равен нулю.^

£5 процессах массообмена между фазами, при отсутствии химиче­ского взаимодействия компонентов системы, фактором:., интенсивности является химическийпотенциал [а. В условиях равновесия фаз в отношении распределяемого компонента числовые значения химического потенциала этого компонента в обеих фазах должны быть равны между собой.

В однокомпонентных фазах величина химического потенциала равна изобарному потенциалу ZK. Химический потенциал любого компо­нента в многокомпонентной фазе равен парциальному значению изобар­ного потенциала этого компонента в данной фазе и для любого компо­нента смеси идеальных газов определяется как:

^KZK + Kf\NpK^- (3-5)

Где kZK—значение изобарного потенциала для одного моля при давлении р = \ ата в ккал! кг-мол\ #=1,987 ккал! кг-мол-°К—газовая постоянная; Т—абсолютная температура газа в °К;

Рк—парциальное давление данного компонента в смеси в долях от

Общего давления. ДЛя реальных газов, к которым неприменимы законы идеальных газов, в уравнении (3—5) парциальное давление заменяется парциаль­ной фугитивностью fK[1] данного компонента"в смеси.

Уравнение (3—5) показывает, что чем выше при данной темпера­туре парциальное давление данного компонента в газе, тем выше значе­ние его химического потенциала и тем самым выше его способность и стремление к выходу из данной фазы. Таким образом, парциальнсе давле­ние данного компонента в газовых бмесях может служить характери­стикой фактора интенсивности и двчукутрн силы пронесся мягсопередачиГ

Для жидких ц твердых компонентов фазовых систем такие простые ©тношения между химическими потенциалами и какими-нибудь другими свойствами или параметрами неизвестны, однако при небольших давле­ниях и в этих случаях можно считать, что парциальное давление насы­щенного пара данного компонента может служить характеристикой хими­ческого потенциала компонента не только в парах, но и в равновесном с ним твердом теле или жидкости.

Правило фаз. Существование данной фазы в системе или равно­весие фаз возможны лишь в определенных условиях; при изменении этих условий равновесие системы нарушается, происходит сдвиг фаз или переход вещества из одной фазы в другую."

Возможность существования данной фазы в равновесии с другими определяется правилом фаз, или законом равновесия фаз.

Условия, при которых система находится в равновесии, могут меняться (система может находиться при разных температурах, давлениях и концентрациях). Условимся называть составной частью системы, или компонентом, каждое из содержащихся в ней химически однородных веществ, которое выделяется из нее и может существовать в изолирован­ном виде длительное время. Компоненты системы, наименьшее число кото­рых достаточно для образования всех фаз данной системы, называют независимыми компонентами.

Правило фаз в общем виде выражается уравнением

С Ф «= k + п (3—6)

Где С—число степеней свободы или минимальное число факторов, кото­рые можно изменять независимо друг от друга без нарушения равновесия данной системы;

Ф—число фаз системы;

K—число независимых компонентов системы;

П—число внешних факторов, влияющих на положение равновесия в данной системе.

Правило фаз формулируется так: сумма числа степеней свободы системы и числа фаз равна сумме числа независимых компонентов и числа внешних фак­торов, влияющих на равновесие этой системы.

Применительно к процессам массопередачи внешними факторами, влияющими на равновесие системы, являются лишь температура и давле­ние, поэтому п== 2 и правило фаз принимает такой вид:

C = k — Ф+2 (3—6а)

Т. е. число степеней свободы равновесной терме - динамической системы, на которую из. внеш­них факторов влияют только температура и давление, равно числу независимых компо­нентов системы минус число фаз системы плюс два.

В зависимости от числа степеней свободы, системы могут быть: безвариантными (при С=0), одновариантными (С=1), двухвариант - ными (С= 2) и многовариантными (С>2).

Однокомпонентные системы. Если система состоит только из одного компонента, т. е. представляет собой чистое индивидуальное вещество, то возможность одновременного существования всех трех фаз—твердой, жидкой и газообразной, по правилу фаз определяется отсутствием степе­ней свободы, так как в этом случае

С= 1 —3 + 2=0

И система безвариантна. Такая система может существовать только при строго определенных значениях температуры и давления (для воды ^=0,0075°С и р=4,579 мм рт. ст.). Изменение любого из этих условий

Приводит к исчезновению одной из фаз и система становится двухфазной.

Наиболее интересной однокомпонент - ной системой является двухфазная систе­ма—жидкость и насыщенный пар. В этом случае

С=1—2+2=1

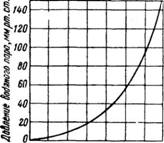
И система является одновариантной. Следо­вательно, не нарушая фазового равновесия, можно произвольно менять либо темпера­туру, либо давление. В таких системах стро­го однозначна зависимость между темпера­турой и давлением насыщенного пара. По­этому при изменении температуры пара одновременно будет соответственно меняться давление и, наоборот, при изменении дав­ления соответственно меняется и температура; для каждой жидкости можно, таким образом, построить кривую давления насыщенного па­ра. В качестве примера приводится кривая давления водяного пара (рис. 308). ^

Для проведения диффузионных процессов необходимо знать зави­симость от температуры давления паров чистых жидкостей, входящих в состав смесей. Обычно такие кривые строят на основании опытных дан­ных, которые для многих жидкостей приведены в литературе. Однако нередко приходится вычислять давление паров чистых жидкостей по тео­ретическим зависимостям или косвенными методами.

При любом равновесном переходе вещества из одной фазы в дру­гую соблюдается зависимость, выражаемая уравнением Клаузиуса—Кла­пейрона

R = ATdЈ ДІЛ

Где г—теплота фазового перехода (испарения, плавления, субли­

Мации и др.) в ккал! кг-мол\

А = ^ —тепловой эквивалент работы в ккал/кгс

Т—абсолютная температура фазового перехода в °К;

Р—давление в кгс/м2;

Д1/—изменение, мольного объема вещества при фазовом пере­ходе в м3/кг-мол.

Применительно к двухфазной системе жидкость—пар перепишем это уравнение так:

DP г (3—7)

А(Уп-Уж)Т

Где /-—теплота испарения при данной температуре в ккал! кг-мол\ Vn—молярный объем пара в м3/кг-мол; Уж—молярный объем жидкости в м3(кг-мол.

В области невысоких давлений пара молярный объем жидкости исчезающе мал по сравнению с молярным объемом пара, поэтому без большой погрешности можно величиной Уж пренебречь, принимая Кж=0. Тогда

AVn = -^

Где R= 1,99 ккал! кг-мол ■ °К.

При этих условиях уравнение (3—7) принимает следующий вид:

DP___ Г Р DT RT*

Или

DP __RdT ,Q 7 )

ИЛИ

D\NP = ~DT (3-76)

При небольших интервалах температур величина г имеет примерно постоянное значение. Тогда интегрирование уравнения (3—76) дает

In Я =--- Jp+C (3—7в)

Где С—постоянная интегрирования.

По уравнению (3—7в) удобно вести практические расчеты, так как оно является уравнением прямой зависимости логарифма давления от обратной величины абсолютной температуры. Если для какой-либо одной температуры Т известно давление Р, то, зная величину г, можно из уравне­ния (3—7в) найти числовое значение константы С, после чего построить

Прямую в координатах lgP, у и по ней находить значение Р для любых

Других температур.

Если величина г также1 неизвестна, то для построения диаграммы необходимо знать давления при двух температурах, составить два урав­нения и, решая их, определить значения г и С.

Уравнение (3—7а) можно интегрировать в пределах от Тх до Т2 и соответственно от Рг до Р2\ тогда получим новое уравнение для опре­деления давления насыщенных паров в зависимости от температуры:

InA ' / L--M (3—8)

R тг

Исходя из условия прямолинейности функции, можно построить диаграмму, связывающую давление пара любого вещества с давлением пара некоторого стандартного вещества.

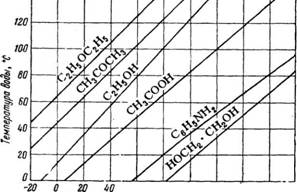
Отложим по оси ординат (рис. 309) температуру кипения стан­дартного вещества (воды), а по оси - абсцисс—температуру кипения различных веществ, при которых давление их пара такое же, как и пара стандартного вещества. Линии постоянного давления, которые соединяют температуры кипения данных веществ, соответствующие температуре кипения стандартного вещества при том же давлении, изображаются на
диаграмме в виде прямых. Так, например, пары анилина при 80° имеют такое же давление, как и пары воды при 20°, и если последнее известно, то может быть определено и давление паров анилина при 80°.

Для удобства пользования диаграммой рис. 309 строится дополни­тельно диаграмма зависимости давления водяного пара от температуры (рис. 310). По этой диаграмме находят, например, что при 20° давление пара воды равно 18 мм рт. ст.; это и будет давлением паров анилина при 80°. Так как прямая может быть построена по двум точкам, то для нанесения на диаграмму линии температур кипения данного вещества необходимо

Знать по крайней мере

Ш\------ г------------------ —-г-—тп—7-і------------- гт— две температуры кипения

При двух соответствую­щих давлениях. При этом одной точкой может слу­жить обычно известная температура кипения ве­щества при 760 мм рт. ст., а второй любая другая температура при любом другом давлении. Если вторая температура неиз­вестна, то ее можно опреде­лить по уравнению (3—8).

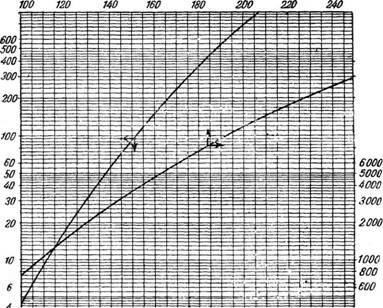
Существует и дру­гой, более точный метод построения кривой зави­симости давления пара от температуры. По оси ординат (шкала логариф­мическая) откладывают давления, а по оси абсцисс — соответствую­щие температуры (рис. 311); шкала оси абсцисс неравномерна, и ее масштаб подобран так, что зависимость логарифма давления некоторого стандартного вещества (воДы) от температуры выражается прямой ли­нией.

После построения линии для воды наносят линии для паров других веществ.

Преимущество такой диаграммы заключается в том, что для близ­ких друг к другу веществ одного и того же гомологического ряда линии температур кипения сходятся в одной точке. Поэтому, если данное веще­ство принадлежит к группе веществ, имеющих общую точку, то доста­точно определить экспериментально лишь одну точку (температуру кипе­ния при 760 мм рт. ст.),- а второй служит общая для всей группы точка пересечения линий.

Двухкомпонентные системы. Если система состоит из двух или боль­шего числа компонентов, то ее положение и равновесие зависят не только от температуры и давления, но и от количественного состава фаз.

Двухкомпонентная система, состоящая из двух фаз, по правилу фаз имеет две степени свободы:

С = K — Ф -J- 2=2 — 2 + 2 = 2

Что означает, что в таких системах можно без нарушения равновесия фаз менять одновременно два фактора—температуру и давление. Для характеристики равновесного состояния этих систем один из факторов принимают постоянным, и тогда зависимость между другим фактором и составом фаз становится однозначной, т. е. при постоянном давлении

Температура, °С

Каждой температуре, а при постоянной температуре каждому давлению соответствуют строго определенные составы фаз.

Более подробно свойства двухкомпонентных систем будут рассмо­трены ниже применительно к конкретным диффузионным процессам, здесь же остановимся на общей функциональной зависимости между рав­новесными составами фаз.

Закон Генри. Равновесный состав фаз в системах газ—раствор газа в жидкости определяется для идеальных газов по закону Генри. По закону Генри парциальное давление растворенного идеального газа про­порционально его молярной доле в растворе:

Р = Цх (3-9)

Или растворимость идеального газа в жидкостях при данной темпера­туре пропорциональна его парциальному давлению над жидкостью, т. е.

Х = ~р (3—9а)

Где х—молярная доля газа в растворе; - Ф—коэффициент пропорциональности, называемый коэффициентом Генри;

Р—парциальное давление газа над раствором. Размерность ф и его числовые значения для каждого данного газа зависят от свойств газа и жидкости, в которой газ растворяется, и от принятой системы единиц.

Если г/р—молярное равновесное содержание данного компонента в газовой смеси и Р—общее давление в системе, то парциальное давле­ние можно выразить равенством

Р = УРр

Подставив это значение р в уравнение (3—9), получим

__ Р_

Х— ф УР

Откуда

(3-Ю)

Или

0p = *i*\J (3—10а)

Где kx = -~—коэффициент распределения, или константа фазового

Равновесия, величина безразмерная. Уравнение (3—10а) показывает, что для идеальных газов равно­весная зависимость между содержанием данного компонента газовой смеси в газе и в жидкости выражается прямой линией, проходящей через основание осей координат и имеющей угол наклона, тангенс которого равен kv

Фазовое равновесие между раствором идеального газа в жидкости и газовой смесью над жидкостью подчиняется закону Генри только при температурах выше критических.

Закон Рауля. Когда температура газа ниже критической, система будет двухфазной: жидкость—насыщенный пар; равновесие такой системы характеризуется составом жидкости х и составом находящегося в равновесии с жидкостью насыщенного пара ур.

Фазовое равновесие жидких идеальных растворов подчиняется закону Рауля, по ксторому парциальное давление любого компонента в парах над смесью жидкостей рав­но упругости насыщенного пара этого компо­нента (при данной температуре), умноженной на его молекулярную долю в жидкости:

Рк = Р«х

Где рк—парциальное давление данного компонента в парах над жидко­стью, выраженное в долях от общего давления; Рк—упругость паров чистого данного компонента при данной тем­пературе;

Л:—молекулярная доля данного компонента в жидкости. Для любого компонента парциальное давление

Р = УРР

И, 4следовательно,

(3-11)

По закону Дальтона для двухкомпонентной системы, состоящей из компонентов А и В

Р = ра + Ре

Или

Р=Рах + Рв(\-х) Подставив найденное значение Р в уравнение (3—11), получим

РАХ

Ур = РАХ+РВ{1-Х) (3-12)

Деля числитель и знаменатель правой части уравнения (3—12) на Рв, получим

Ур = 1+/(а-1) (3~13>

РА '

Где а= - g--------- относительная летучесть компонентов смеси.

В

Уравнение (3—13) показывает, что для идеальных растворов равно­весная зависимость между составами жидкости и пара над жидкостью выражается гиперболойL проходящей через основание (х=0) и вер­шину (х=1) прямоугольной системы осей координат.

В тех же случаях, когда для равновесной системы не действи­тельны приведенные выше законы фазового равновесия, зависимость между составом пара над жидкостью и составом жидкости может быть найдена только опытным путем и в общем случае выражается урав­нением

YP = F(X) (3-14)

І или

Ур = Ах» (3-15)

Однако и в этом случае на диаграмму у—х может быть нанесена кривая равновесия по опытным данным, которые для многих жидкостей приведены в справочной и специальной литературе.