АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Центробежные насосы
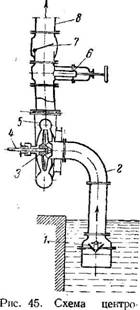
Принцип действия. В центробежных насосах всасывание и нагнетание жидкости происходит под действием центробежной силы, возникающей при вращении заключенного в корпус колеса с лопатками (рис. 45).
В чугунном корпусе 5 спиралевидной формы вращается вал приводимый в движение непосредственно от электродвигателя или от трансмиссии; на валу закреплено рабочее колесо 3 с лопатками определенной формы, образующими между собой каналы для прохода жидкости.
Корпус насоса снабжен двумя штуцерами. Один находится на осевой части корпуса и непосредственно сообщается с пространством внутренней окружности колеса; к этому штуцеру присоединен всасывающий трубопровод 2. Второй штуцер помещен тангенциально на боковой части корпуса и соединяется с нагнетательным тр убоп р оводом 8.
Приемный клапан служит для того, чтобы залить насос жидкостью перед пуском и предотвратить опоражнивание всасывающего трубопровода (при остановке насоса). Чтобы предотвратить обратный слив жидкости и защитить насос от гидравлического удара при внезапной остановке, в напорном трубопроводе часто устанавливают обратный клапан 7.
Если внутреннее пространство корпуса заполнено жидкостью, то при вращении колеса лопатки придают жидкости, находящейся в колесе, вращательное движение. При этом возникающая при вращении центробежная сила отбрасывает жидкость от центра к периферии колеса; отсюда она затем выбрасывается в корпус и поступает в нагнетательный трубопровод 8.
При вращении колеса жидкость непрерывно засасывается из бассейна или резервуара в насос и выталкивается из насоса. Таким образом, ь центробежном насосе, в отличие от поршневого, всасывание и нагнетание жидкости протекают равномерно и непрерывно.
Давление, развиваемое центробежной силой в насосе, а следовательно, и высота нагнетания зависят от скорости вращения рабочего колеса и будут тем больше, чем большее число оборотов делает колесо.
Высота подачи центробежного насоса с одним рабочим колесом органичена. Поэтому насосы в зависимости от требуемой высоты подачи изготавливают с несколькими рабочими колесами, соединенными друг с другом последовательно.
По числу рабочих колес, соединенных последовательно в одном корпусе, различают насосы: одноступенчатые и многоступенчатые.
|
Бежного насоса: /—приемный клапан; 2—всасы" вающий трубопровод; 3—рабочее колесо; 4- вал; 5—корпус; б—задвижка; 7—обратный клапан; в—нагнетательный трубопровод. |
Движение жидкости в насосе. Проходя по каналу между лопатками рабочего колеса, жидкость совершает сложное движение: с одной стороны, она движется вдоль канала внутри рабочего колеса к его наружной окружности, т. е. в радиальном направлении, а с другой стороны, она получает движение по направлению вращения колеса.
Обозначим:
Wt и w2 — скорость движения жидкости во всасывающем и нагнетательном трубопроводах в м/сек; w' и w'2—относительная скорость жидкости при входе в канал и выходе из канала между лопатками в м/сек; гх и г2 — радиус внутренней и наружной окружности колеса в м; fi и /2 — сечение канала между лопатками при входе и выходе жидкости в ж2. п—число оборотов колеса в минуту. Количество жидкости, проходящей через канал в 1 сек.:
Усек. = = f2W2
А так как в центробежных насосах сечение канала на внешней окружности колеса всегда больше сечения его на внутренней окружности, т. е.
H>fl, то w'2<w\. г
|
|
|
«і = - g^- м/сек На наружной окружности колеса 2г, г2п. «2 = fin •м/сек |
|
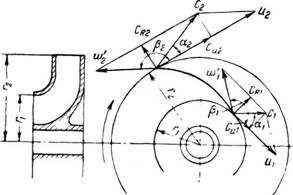
Рис 46. Скорость жидкости в рабочем колесе центробежного насоса. |
Скорости wi и w2 жидкость имела бы в том случае, если бы колесо насоса находилось в состоянии покоя. При вращении колеса жидкость получает окружную скорость: на внутренней окружности колеса
Абсолютная скорость жидкости, которую обозначим через сх при входе в колесо и через сг— при выходе из колеса, является равнодействующей радиальной и окружной скоростей и может быть найдена по правилу сложения скоростей.
Рассмотрим скорости жидкости на входе в рабочее колесо и выходе из него (рис. 46). Построив параллелограмм скоростей, находим скорость сх при входе жидкости в рабочее колесо, направленную под углом а,, и скорость сг при выходе жидкости из рабочего колеса, направленную под углом я2.
Для того чтобы жидкость поступала в колесо без толчков, приводящих к большим потерям напора, она должна вступать на лопатку рабочего колеса под углом а,. Поэтому в большинстве случаев лопатки делают не прямыми, а загнутыми назад, причем угол аг принимают равным 90°. Во избежание потерь напора из-за толчков жидкость должна покидать лопатку под углом а2; величину угла а2 принимают равной от 10 до 15°.
При переходе жидкости из канала в корпус происходит значительное снижение скорости, вследствие чего кинетическая энергия движения жидкости превращается в потенциальную энергию давления, т. е.
Происходит превращение скорости в давление, необходимое для подачи жидкости на заданную высоту. При переходе жидкости с лопаток рабочего колеса в неподвижный корпус возникают гидравлические удары,
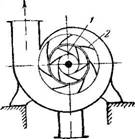
Которые обусловливают большие потери напора, возрастающие со скоростью выхода жидкости из колеса. Для уменьшения потерь рабочее колесо снабжают направляющим аппаратом (рис. 47), который окружает рабочее колесо и имеет каналы примерно такой же формы, что и каналы рабочего колеса, но изгиб каналов направляющего аппарата имеет направление, обратное изгибу каналов рабочего колеса. При наличии направляющего аппарата преобразование скорости жидкости в давление протекает равномерно и постепенно, в результате чего жидкость проходит корпус с небольшими скоростями и при высоком давлении, а следовательно, и с небольшими потерями напора.
|
Рис. 47. Центробежный насос с направляющим аппаратом: |
|
/—рабочее квлесо; 2—направляющий аппарат. |
Основное уравнение центробежного насоса. При вращении рабочего колеса жидкость под действием центробежной силы отбрасывается от центра колеса к его периферии. Если обозначить через о> угловую ско - расть вращения колеса в радианах, то получим следующее общее выражение центробежной силы:
С — тш2г кгс
Работа, совершаемая центробежной силой на элементе пути dr,
Равна
DT — rrwPr dr кгс - м
При прохождении жидкостью в радиальном направлении пути, равного г2—гх, общее количество энергии, сообщаемое жидкости центробежной силой, составит
Г%
|
М |
Т = j /720)2,- ф. = w2 (/f — rf) кгс -
Но
Следовательно,
Т = -^-(«2 —U2J кгс. м Масса 1 кг жидкости
Tn
Поэтому 1 кгс жидкости при прохождении через рабочее колесо воспринимает количество энергии:
— кгс - м/ кгс
Если бы рабочее колесо находилось в состоянии покоя, то при отсутствии потерь общее количество энергии при движении жидкости
через колесо оставалось бы неизменным и по уравнению Бернулли при г1=г2=0 (для 1 ккг жидкости)
Pi , (WlY _ Р2 | W
У 2g У 2 G
Где рх—давление жидкости при входе в рабочее колесо в кгс/м2;
Р2—давление жидкости при выходе из рабочего колеса в кгс/м2. Действие центробежной силы при вращении колеса ведет к приращению общего количества энергии жидкости на величину
2 2 «2 — «і
Т =
2g
И, следовательно, в этом случае будет иметь место равенство
Рг + МІ і в Ж I М*
Y ' 2G У ^ 2G
Откуда и находим давление в канале
Р Ft-Pi ^ 4-А. (W'I)2~(4)2 ,дч
Y Y 2G 2 G
При наличии потерь высота напора жидкости при входе ее в рабочее колесо
Ж—P-L И ^ y y 1 2g ^ 2g +
А высота напора при выходе из рабочего колеса
Р*__ и і Pa 4 ,
— П2 + — 2g + + ~2g
Вычитая почленно правые и левые части этих двух уравнений (имея в виду, что практически wx—w2), получим
Pv — Pl y
Где
2g~ ~ ^ ~2G~ +
Сравнив последнее уравнение с уравнением (А), окончательно получим
Сі— Cf Ul —И2, -J-Fou)2
- - !;2T = ^2i-L+^2FX+ 2g <Б>
Из параллелограмма скоростей при входе и выходе (см. рис. 46) находим:
(w\y — и\ - f с\ — 2ихсг cos ах (w'2y = и\ + с\ — 2 и2с2 cos а2
Подставив эти значения в уравнение (Б) и проведя соответствующие преобразования, получим
Jj ___ и2с2 cos а2 — ихсх cos а. г ^g^
Так как в центробежных насосах угол ах=90о, то cos 04=0 и напор
Н = u*c*c°sa* = 1 и2си2 (1—121)
Где с^ = с2 cos а2—проекция абсолютной скорости при выходе жидкости из насоса на направление окружной скорости жидкости (см. рис. 46).
Уравнение (8) было выведено JI. Эйлером и носит название о с - новного уравнения центробежного насоса.
Высота напора центробежного насоса в значительной степени зависит от формы лопатки рабочего колеса или от величины угла р между направлениями окружной и относительной скорости.
Из параллелограмма скоростей в рабочем колесе (см. рис. 46) находим
Сиг = и2 — cr2 ctg (180 — (У = и2 + cRi ctg р2
Подставляя это значение cU2 в уравнение (1 —121), получим
Uo 4- щеп ctg в, Н = 2 (1—121а)
8
Если лопатки загнуты вперед, то р2<90°, CRa'ctg j32 имеет положительное значение и
И 9
Я> —
G
Если лопатки загнуты назад, то р2>90°, cRj! ctg (32 будет иметь отрицательное значение и
Ыо
8
Наконец, если лопатки расположены радиально, то (За=90°, .cR2ctgp2=0 и
8 к
Таким образом, теоретически наибольший напор может быть достигнут, если лопатки загнуты вперед, и наименьший—если загнуты назад. Несмотря на это, практически предпочитают применять лопатки, загнутые назад, так как в этом случае потери напора будут наименьшими.
Фактическая высота напора, так же как и в поршневых насосах, буеет меньше теоретической вследствие гидравлических сопротивлений е самом насосе, и действительный напор, развиваемый насосом, будет равен
Не=,-г}гН (1—121в)
|
* Ра гг yr W\ — —----------------------------- К |
Высота всасывания. По предыдущему давление жидкости при входе в рабочее колесо выражается равенством
TOC \o "1-3" \h \z 2 2 V, W.
____________ J___ vr __ L
У Y " ЖД1 ' 2g ^ 2g
Из которого определяется высота всасывания
Pa Pi с\-
Н1 = —---------- —-------- ^— ес - р -
Y Y 2 g 2 g
В данном случае давление pt обусловливается давлением паров жидкости. Если при f упругость паров жидкости равна рж, то
(1-122)
Y Y 2 g v
Это уравнение показывает, что высота всасывания центробежного насоса, так же как и поршневого, зависит от скорости протекания жидкости и сопротивлений в линии всасывания, а также от температуры перекачиваемой жидкости.
С повышением температуры возрастает противодавление паров и растворенного в жидкости воздуха, выделившегося из нее вследствие разрежения, в результате чего высота всасывания насоса уменьшается.
Для увеличения высоты всасывания следует обеспечить полную герметичность всасывающего трубопровода и небольшую потерю напора в нем.
Для перекачивания горячих жидкостей насос следует располагать ниже уровня жидкости в приемном резервуаре.
Практически высота всасывания у центробежных насосов при перекачивании воды не превышает следующих величин:
Температура в °С. . . 10 20 30 40 50 60 65 Высота всасывания в м 6543210
В отдельных случаях при перекачивании воды высота всасывания может быть выше указанной.
Высота всасывания центробежных насосов относительно выше, чем поршневых, так как отсутствуют потери на преодоление сил инерции. Однако для Того чтобы центробежный насос всасывал жидкость, линия всасывания и насос перед пуском его в ход должны быть залиты жидкостью. В противном случае рабочее колесо будет вращаться в воздушной среде и не создаст разрежения, достаточного для подъема жидкости с нижнего уровня в насос.
Если давление внутри насоса становится равным, упругости паров жидкости при данной температуре, то в нем происходит интенсивное парообразование, выделение растворенного в жидкости воздуха и отрыв жидкости от лопаток колеса. Наступает явление кавитации, сопряженное с резким падением производительности и к. п. д. насоса и возникновением ударов, разрушающих колесо и корпус насоса.
Для предупреждения кавитации необходимо правильно выбирать высоту всасывания, понижать температуру жидкости и создавать подпор при перекачивании горячей жидкости.
Для учета явления кавитации при определении высоты всасывания центробежного насоса в правую часть уравнения (1—122) вводят дополнительно так называемый коэффициент кавитации:
2_
J = 0,00123 (V™-n*>3 м (1—222а)
ГІ
Где 1/сек.—производительность насоса в м3/сек\ п—число оборотов в минуту; Н—напор, развиваемый насосом в м.
При этом высота всасывания центробежного насоса выразится уравнением
Производительность, мощность на валу насоса и коэффициент полезного действия. Производительность центробежного насоса зависит от относительной скорости протекания жидкости по каналам рабочего колеса, а также от ширины и диаметра рабочего колеса:
^сек. = bx {kDx — 82) w\ = b.2 (*D2 — oz) w'2 мЧсек
Где Dx—внутренний диаметр рабочего колеса в м; D2—наружный диаметр рабочего колеса в м\ Ьх—ширина колеса на внутренней его окружности в м; Ь2—ширина колеса на внешней его окружности в ж; 8—толщина лопаток колеса в м; z—число лопаток в рабочем колесе. При радиальном расположении лопаток колеса
W\ е= сх sin а. х и w'2 = с2 sin а2
И, следовательно, производительность центробежного насоса выразится уравнением
0.4ас = 3600 [TiDx — bz) qsin»! = 3600 [tzD2 — ог) c2sina2 мЧчас (1—123)
Скорость сх принимают равной скорости жидкости во всасывающем трубопроводе.
Мощность на валу центробежного насоса находят по тем же формулам, что и для поршневых насосов:
Где Qe—производительность насоса в м3/час (Qe—rj0Q); ті—полный к. п. д., равный 0,6—0,8. Характеристики насосов. Машиностроительные заводы выпускают центробежные насосы на определенные значения производительности (Qe), высоты напора (Не), числа оборотов (п) и мощности (Ne). При этих значениях насос должен работать с наибольшим к. п. д. (tj).
Однако весьма часто в эксплуатационных условиях приходится устанавливать насосы для работы при других значениях Qe или Не1 но изменение величины производительности или напора неизбежно влечет за собой изменение и других параметров, характеризующих насос.
Теоретически зависимость между Qe, Не, Ne и п может быть выражена следующим образом:
Qe ___ JL • Не __ / " V ■ - ( П Y і 1 194V
Т. е. производительность насоса изменяется пропорционально числу оборотов, высота напора—пропорционально второй степени числа оборотов, а мощность—пропорционально третьей степени числа оборотов.
Практически такой строгой зависимости между параметрами насоса нет. Кроме того, с изменением отдельных параметров изменяееся, как уже было отмечено выше, и к. п. д. насоса. Поэтому для каждого типа насосов необходимо определять эту зависимость опытным путем.
Зависимость между напором Не, мощностью Ne, к. п. д. т] насоса и его производительностью Qe при постоянном числе оборотов п выражается графически и носит название характеристики насоса.
Зная характеристику насоса, можно выбрать наиболее благоприятный режим его работы в эксплуатационных условиях.
Для составления опытной характеристики измеряют величины Qe и Не при п—const и переменном режиме работы насоса, достигаемом путем постепенного открытия задвижки на напорном трубопроводе; одновременно измеряют расхо - u дуемую на валу насоса мощ - ^ /оНем v ность. Затем подсчитывают значения к. п. д. насоса и строят кривые Qe—Не, Qe—Ne и Q-ri (рис. 48).
|
Расход в пределах Qe=600—1200 л! сек соответственно 85—60 м. |
|
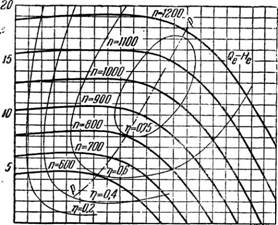
Е, равных Насосы периодически испытывают на заводе-изготовителе при различных числах оборотов и строят опытные универсальные их характеристики (рис. 49)—графики, на которых нанесены за- Висимости Qe—He при разных п— const. Пользуясь универсальной характеристикой, можно легко установить пределы рационального применения насоса в данных условиях и выбрать наиболее благоприятный режим его работы. По универсальной характеристике, приведенной на рис. 49. такой режим соответствует точкам, лежащим на кривой р—р, например Qe—105 лісек, Не=\2,Ь м, лг= 1000 об/мин или Qe— 80 л/сек, Не= 7 л, п=750 об/мин и т. д. |
|
/00 Qe л/сєх Рис. 49. Универсальная характеристика центробеж |
|
Ного насоса. |
Из кривых, приведенных на рис. 48, для определенного насоса видно, что при нормальном режиме работы максимальный к. п. д =0,82, производительность Qe=900 л/сек и напор Не= =75 -.г. Мощность на валу насоса будет соответственно Л^=1100 л. с. При работе насоса с к. п. д. не ниже 0,75 можно при данном числе оборотов получать при напорах Н Обычно
0 50 /00 Ш 200
Подобие центробежных насосов. При конструировании центробежных насосов приходится прибегать к экспериментальным исследованиям. Обобщение экспериментальных данных для перехода от опытной модели к промышленным образцам выполняется с применением методов теории подобия. Результаты эксперимента можно обобщить для разных размеров насосов, если соблюдаются следующие условия: геометрическое подобие приточной части насосов; кинематическое подобие потоков на границах, что определяется постоянством отношения скорости
W
Протекания w к окружной скорости лопастного колеса и, т. е. — = const; динами
ческое подобие сил инерции и сил вязкости для рассматриваемых режимов, что определяется равенством числовых значений критерия подобия. При соблюдении - этих условий в сходственных точках потоков сравниваемых насосов скорости пропорциональны и одинаково направлены. —
Принимая за d любой линейный размер проточной части насоса, например какой - либо из диаметров лопастного колеса, имеем на основании теории подобия:
Qe Ёне SNe
~~nd? = const; = conSt: = const
Исключив g, как постоянную величину, получим
Qe ИЕ Ne
Td* = const; nW* = const: = const
Коэффициент быстроходности. Для характеристики геометрически подобных насосов, независимо от их размеров, вводят понятие о коэффициенте быстроходности По - Этот коэффициент равен числу оборотов модельного (удельного) насоса, который геометрически подобен данному и при подаче Qe=7b л/сек развивает напор Не— 1 м.
Для группы геометрически подобных насосов Пб является величиной постоянной.
Коэффициент быстроходности колеса связан с производительностью Qe (м3/сек). напором Не (м) и числом оборотов п следующей зависимостью:
Чем больше коэффициент быстроходности колеса, тем меньше его диаметр D2 {см. рис. 46) и тем меньше отношение наружного диаметра £>а к внутреннему DA. Вместе с тем возрастает отношение ширины выхода Ь2 к наружному диаметру колеса D2.
Поэтому у центробежных насосов с коэффициентом быстроходности Яб>350 изменяется форма рабочего колеса и жидкость движется в них не радиально, а диагонально или параллельно оси насоса (винтовые и пропеллерные насос ы). Такие насосы имеют высокую производительность Qe при малых напор'ах Не и большом числе оборотов п. В химической промышленности пропеллерные насосы применяют для создания циркуляции жидкости в различных аппаратах.