ПРОЦЕССЫ ГРАНУЛИРОВАНИЯ в РОМЫШЛЕННОСТИ
ГРАНУЛИРОВАНИЕ ОКАТЫВАНИЕМ
Окатывание объединяет группу процессов, которые характеризуются перемещением гранулируемого порошка по поверхности аппарата. При этом частицы перекатываются по стенкам аппарата и друг через друга. Агломерация порошков при окатывании была замечена давно и использо* вана для практического осуществления процесса гранулирования. Окатывание можно отнести к нарастающей грануляции — разновидности структурной грануляции [79].
Наглядным примером гранулирования окатыванием является образование снежной лавины. При движении кристаллов льда в глубине их возникают большие давления, что приводит к агломерации и росту агломератов. Особенно благоприятные условия для агломерации кристаллов возникают при плавлении в результате трения отдельных кристаллов; аналогично этому процессу протекает грануло - образование в массе порошка при введении жидкого связующего.
При окатывании из многих возможностей сцепления частиц осуществляются только те, которые обеспечивают относительно большую прочность. Следовательно, происходит выбор самых благоприятных возможностей сцепления, чему способствуют увеличение точек соприкосновения при возможно более плотной укладке частиц.
Непрерывное движение гранулируемого материала приводит как к образованию и росту гранул, так и деструкции наименее прочных из них. При одновременном протекании этих противодействующих процессов образуются и сохраняются прочные и примерно одинаковые гранулы.
При окатывании возможны все основные процессы структурного гранулирования (кроме прессового): сухое, граничное, влажное и образование твердых мостиков. Физикохимическая сущность этих процессов на микроуровне описана выше. Далее рассмотрим кинетику и механизм гранулообразования на макроуровне, который действует при осуществлении любого процесса окатывания.
Простейшим способом гранулирования окатыванием (и наиболее распространенным) является гранулирование в барабанах. Характерные элементы процесса гранулирования в барабанах справедливы и для других способов гранулирования окатыванием. Поэтому кинетику и механизм гранулообразования будем выяснять на примере гранулирования в барабане с вращающимся корпусом.
Типичная схема гранулирования окатыванием выглядит следующим образом. Во вращающийся аппарат (барабанный. тарельчатый, конический), установленный горизонтально или с небольшим наклоном, поступает порошок, обычно орошаемый на входе связующей жидкостью. Смоченные частички агломерируются и, окатываясь, приобретают необходимые плотности и размерь1. Но возможны отклонения от нормального роста гранул в результате соединения отдельных гранул друг с другом, а также деструкции их. Необходимо избегать этих отклонений, ухудшающих качество гранул.
При вращении барабана часть порошка захватывается его стенкой и поднимается на некоторую высоту, а затем падает или сползает вниз. Высота подъема и количество захваченного порошка зависят от нескольких факторов: отношения величин внутреннего и внешнего трения, скорости вращения, степени заполнения барабана. При подъеме гранулы движутся совместно с барабаном, не перемещаясь друг относительно друга до определенной точки, где начинается скатывание, в процессе которого гранулы увеличивают размеры, формуются и уплотняются. Для гранулируемого материала процесс окатывания, осуществляется ли он по периодической или непрерывной схеме, всегда является циклическим в смысле роста частиц.
В смесительных барабанах установлены три режима движения сыпучей массы в зависимости от степени заполнения и скорости вращения [331: колебательный, при котором материал поднимается вместе со стенкой барабана на некоторую высоту и затем соскальзывает (при гранулировании скатывается) по ней вниз; наблюдается это при степени заполнения, равной 0,03; режим проскальзывания, при котором материал остается неподвижным, полностью проскальзывает по стенкам корпуса, наклоняя свою свободную поверхность на некоторый угол к горизонту; для этого режима степень заполнения составляет 0,03 — 0,1; циркуляционный, для которого характерна интенсивная циркуляция в поперечном сечении слоя вследствие подъема материала на некоторый угол со стенкой корпуса и обрушивания его вниз по наклонной поверхности слоя. Этот режим возможен при степени заполнения 0,1—0,8.
Для грануляторов, как и для смесителей, характерны те же режимы работы, но при иных степенях заполнения аппаратов. Промышленные грануляторы барабанного типа, как и промышленные смесители, в основном работают в третьем режиме.
По мере продвижения гранулируемого материала от места загрузки к разгрузочному концу рост гранул замедляется и практически прекращается при достижении определенного размера, равного размеру гранул, выходящих из
гранулятора. Конечная величина гранул зависит от свойств гранулируемых материалов и количества связующего.
Кинетика процесса. Большой интерес представляет выяснение скорости роста гранул, т. е. установление кинетических зависимостей процесса.
 |
 |
В работе [74] рассмотрен процесс образования гранул •определенного размера (4 мм) из тонкоизмельченной извести в широком диапазоне низкого содержания влаги и низких •скоростей роста гранул. Процесс проводился по перио-
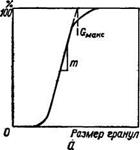
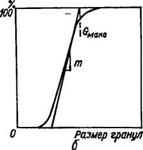
Рис. 9. Распределение гранул по крупности: а — при низком содержании влаги н низких скоростях роста гра« нул; б — при высоком содержании влаги и больших скоростях роста гранул.
дической схеме. В результате было установлено, что дисперсность гранул или, что то же самое, распределение гранул по крупности происходит самопроизвольно.
На рис. 9,а графически отображено распределение гранул по крупности при периодическом окатывании, которое может характеризоваться наклоном т прямой части и отрезком бмако экстраполированной части кривой. Установлено, что величина тбмако не изменяется при увеличении размеров гранул. Проведенный математический анализ подтвердил, что это соотношение согласуется с ростом гранул посредством беспорядочного слипания более мелких гранул, а также двух гранул, различных по величине.
Для получения гранул размерами 4—5 мм при низком содержании влаги потребовалось несколько сотен оборотов барабана. При высоком содержании влаги значительно более крупные гранулы (диаметром до 25 мм) получены при таком же количестве оборотов барабана [741. В ходе эксперимента по получению крупных гранул песка установ-
лено, что первоначальный рост наблюдается в результате слипания агломератов, а последующий — при дроблении - самых мелких гранул, обломки которых слипаются с крупными гранулами. При этом более крупные гранулы растут быстрее. Математический анализ показал, что самопроизвольное распределение гранул по крупности при низком содержании влаги подобно росту гранул при дроблении мелких гранул с последующим присоединением к крупным гранулам при высоком содержании влаги.
Как видно из рис. 9, б, где графически - отображено распределение гранул по величине при высоком содержании влаги, прямая часть кривой также характеризуется величиной mGMaKс, что подтверждает аналогичность кинетических зависимостей при различных механизмах и условиях протекания процессов.
Аналитически скорость роста гранул можно характеризовать выражением
Xt = X0em<w-w*, (75)
где Х0 — размер исходных гранул, соответствующих W0; Xt — размер гранул; — исходное содержание влаги; W — конечное содержание влаги; т — чувствительность гранулируемых материалов к изменению содержания влаги (т, Х0 и W0 определяются экспериментально и характеризуют гранулируемость материала).
Данная экспоненциальная зависимость установлена в результате проводившихся в МИХМ исследований процессов гранулирования суперфосфата, смеси фосфоритной муки с хлористым калием, электроугольных материалов и металлических порошков. Она позволяет определить средний размер гранул, выходящих из гранулятора при установившемся режиме работы. Выведенные эмпирические зависимости являются основой для установления более общих аналитических зависимостей.
Кинетика процесса в пусковом периоде исследовалась при следующих допущениях: смесь состоит из исходных мелкодисперсных частиц, некоторого количества мелких гранул (ретура) и жидкого связующего; разрушение гранул и агломерация их отсутствуют; подача материала осуществляется только в зоне загрузочного конца барабана. При этих допущениях в начале работы гранулятора средний размер выходящих гранул изменяется от размера ретура,
загружаемого в аппарат перед пуском, до размера, определенного выражением (75). Если подача материала непрерывная. то размер выходящих гранул будет оставаться тем же, а количество гранул, участвующих в процессе, остается неизменным. Поэтому количество мелкодисперсного материала, подаваемого на гранулирование,

G„_G,[1-(i=-)’], (7(9
Интегрирование уравнения при граничных условиях х — = х_ при т =* 0 и х = х, при т *=» / приводит к виду
Это выражение позволяет определить средний размер гранул на выходе из гранулятора в любой момент от начала гранулирования до выхода на режим, т. е. пусковой период. Ею можно пользоваться при расчете размера гранул, получаемых при периодическом гранулировании.
Знание кинетических зависимостей позволяет определить не только средний размер гранул на выходе, но и дисперсность гранулята (гранулометрический состав), что очень важно при практическом применении процесса гранулирования. В работах Н. А. Шаховой показано, что расчет гранулометрического состава продукта основывается на совместном решении уравнения кинетики процесса и уравнения распределения времени пребывания материала в грануляторе [34; 711.
В результате .проведения промышленных исследований выяснено, что отклонение времени пребывания отдельных гранул в барабанных аппаратах от среднего не превышает 8%. Отсюда следует, что с точностью до 8% гранулы ретура вырастут в аппарате на одинаковую величину и кри
вая дисперсности гранулята будет подобна кривой дисперсности ретура, но сдвинута на величину среднего приращения гранул, которая в установившемся режиме работы гранулятора определяется по уравнению (75), а в пусковой период и при периодическом гранулировании — по уравнению (78).
 Механизм граиулообразования. При любом режиме работы, т. е. характере движения материала в барабане, образование единичных гранул осуществляется по одной схеме. Выше были разобраны силы и факторы, определяющие связывание частиц в гранулы.
Механизм граиулообразования. При любом режиме работы, т. е. характере движения материала в барабане, образование единичных гранул осуществляется по одной схеме. Выше были разобраны силы и факторы, определяющие связывание частиц в гранулы.
Рассмотрим механизм грану- лообразования при окатывании в результате формования исходных частиц. Подробный анализ этого механизма и его количественные зависимости даны в работе 1811. Для простоты будем считать частицы и гранулы сферическими.
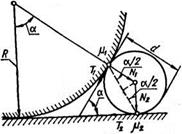
При окатывании частицы Рис,0 Силы, возникающие при увлекаются вниз СИЛОИ тяжес - перекатывании гранулы через ти, при этом гранула до тех частицу,
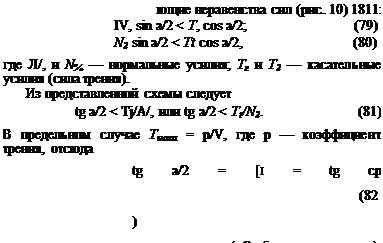 пор перекатывается через малые шарики, не соединяясь с ними, пока действуют следу
пор перекатывается через малые шарики, не соединяясь с ними, пока действуют следу
вначений коэффициента трения: частицы порошка—шарик и частица — стенка гранулятора. Для различных сухих
минералов р составляет от 0,3 до 0,6. Значению р = 0,3 соответствует ф = 16°42' или а = 33°24 Из рис. 10
![]()
 |
cos а =
![]() 2R (1 — cos 2<р) ** 1 - f cos 2? *
2R (1 — cos 2<р) ** 1 - f cos 2? *
При а = 33°42' или cosa = 0,835 предельное значение отношения величин шарика и частицы (при р — 0,3)
При коэффициенте трения р = 0,2 Ь = 12,5.
Итак, получен инструмент для расчета увеличения размеров частиц при окатывании: зная коэффициент трения р, можно сразу определить, во сколько раз возрастет при окатывании размер частиц. Частицы, имеющие размеры менее Rib, проникают в пустоты гранулы, уменьшая ее пористость, и увлекаются ею. Из соотношения b = Rid легко рассчитываются предельные величины частиц, увлекаемых шариками, имеющими определенные размеры: при b = =5,6 и 12,5 шарики радиусом #=0,1 мм увлекают частицы, у которых соответственно d = 0,18 и 0,08 мм, при R = 4 мм d = 0,72 и 0,32 мм; при R = 10 мм d = 1,8 и 0,8 мм.
С возрастанием коэффициента трения увлекаются все большие частицы порошка, так, для р = 0,5 и a = 53°06' b = 2 и dKp„T = RI2. В момент перекатывания гранулы через частицу порошка происходит толчок, уплотняющий гранулу и способствующий проникновению частицы в гранулу, т. е, формованию гранулы.
Для расчета грануляторов окатывания весьма важно уметь определить величину сил взаимодействия частицы и шарика, которую можно рассчитать, исходя из второго закона механики Ньютона:
F = та. (89)
Массу гранулы всегда можем определить, необходимо рассчитать ускорение. Примем, что гранула радиусом R катится без скольжения с угловой скоростью w, скорость поступательного движения
![]() W = Яш.
W = Яш.
Тогда ускорение
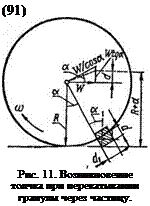 а = Wt — Rwt = Riga,
а = Wt — Rwt = Riga,
откуда (рис. 11)
f=tga/(o. (92)
При перекатывании гранулы по поверхности частицы диаметром d мы считаем неизменной горизонтальную скорость центра тяжести гранулы (W — Riо), но если учесть движение в направлении, составляющем с горизонтальным угол сс, то начальная скорость перекатывания в этом направлении составляет U7/cosa, а вертикальная составляющая начальной скорости U7B =
= Wtga. Отсюда получаем величину начального ускорения в вертикальном направлении
![]() W tg a IW n, W2
W tg a IW n, W2
, = —r2- = Wh> = Rїв® = s-.
|
-Гр-Й-ТїТЯ*. |
|
4 *iR3W2 _ 4 ті пг. у/а 3 g R 3 g W '• |
Величина толчка в вертикальном направлении
|
cos2 a (R-- d) R cos |
Начальное ускорение для поднятия центра тяжести гранулы при диаметре частицы d, по радиусу R + d, со скоростью W/cos а
поскольку, как видно из рис. 11, cos a = R/(R - f d). Тогда полная сила ускорения
f = (98)
Пусть частица на поверхности гранулы имеет поперечное сечение S = ссР, где с — коэффициент. Обозначим bt = = R/du тогда
S = cR2/bl (99)
Давление в месте соприкосновения частицы и шарика
о-т-тт^тО+т)- <|00>
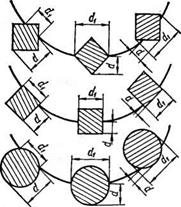 Величина постоянной о зависит от формы частицы или от ее расположения на поверхности гранулы. На рис. 12 показано относительное изменение d и dt по мере внедрения частицы в гранулу: значение г?! увеличивается до тех пор, пока частица не проникнет в гранулу до своей самой большой плоскости поперечного сечения, после этого dt остается постоянным. Обратно пропорционально d1 изменяется значениеЬи аследо - Рис. 12. Схема внедрения частицы вательно, и давление р. Дзв - в гранулу. ление р мало при малом б, и
Величина постоянной о зависит от формы частицы или от ее расположения на поверхности гранулы. На рис. 12 показано относительное изменение d и dt по мере внедрения частицы в гранулу: значение г?! увеличивается до тех пор, пока частица не проникнет в гранулу до своей самой большой плоскости поперечного сечения, после этого dt остается постоянным. Обратно пропорционально d1 изменяется значениеЬи аследо - Рис. 12. Схема внедрения частицы вательно, и давление р. Дзв - в гранулу. ление р мало при малом б, и
больших бис. В предельном случае, при равенстве частицы и гранулы (d = dj, имеем
Р = (Ь* + Ъ) = + * ) • (101)
Наиболее интенсивное формование гранулы происходит тогда, когда центр тяжести ее отклоняется от прежнего
равномерного движения не благодаря перекатке через частицы, а в результате неравномерности самой гранулы. В этом случае возникают как усилия, направленные к центру гранулы, уплотняющие ее, так и срезывающие усилия, способствующие получению гранулой шарообразной формы.
 В работе 181] выведены ценные для разработки барабанных грануляторов количественные зависимости характера движения материала от числа оборотов и степени заполнения аппарата, т. е. уже известных нам режимов работы барабанов. Пусть в барабане, имеющем диаметр D, угловая скорость которого со = лп/30, а окружная скорость вращения U70Kp =
В работе 181] выведены ценные для разработки барабанных грануляторов количественные зависимости характера движения материала от числа оборотов и степени заполнения аппарата, т. е. уже известных нам режимов работы барабанов. Пусть в барабане, имеющем диаметр D, угловая скорость которого со = лп/30, а окружная скорость вращения U70Kp =
= Dco/2 = Олп/60, степень заполнения меньше 0,1. При этом гранулы скатываются без скольжения по стенке барабана с окружной скоростью вращения WOKp после того, как они поднялись на высоту
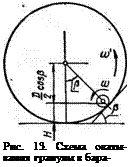
tf = ^-( 1 —eosp). (102)
Касательная, проложенная в этот момент к стенке барабана, образуете горизонталью угол р = arctgp(рис. 13). Если барабан работает при степени заполнения больше 0,1, то большое количество гранул, находящихся в нем, приводит к тому, что верхние ряды гранул скатываются по нижележащим. При этом их скорость будет значительно меньше, чем скорость гранул, скатывающихся по стене.
При расчетах гранулирующих барабанов, как и при расчетах шаровых мельниц, применяют понятие критической скорости вращения
т. е. такой скорости вращения, при которой частицы материала начинают вращаться вместе со стенкой барабана. При этом критическая частота вращения барабана
Для шаровых мельниц оптимальная скорость вращения барабана составляет 75% от критической, т. е.
Лопт = ^. (105)
Для гранулирующих барабанов рекомендуются различные скорости — от 10 до 80% от пкрит.
Роль связующего вещества при окатывании. Окатывание можно осуществлять по схеме сухого гранулирования, однако на практике оно применяется довольно редко. Межмолекулярные силы незначительны и не достигают теоретических значений из-за неровностей поверхности. Сухое окатывание часто сопровождается пылением. Кроме того, необходимо вводить зародыши гранул, так как при равенстве размеров гранулы и частицы они не агломерируются. Поэтому в большинстве случаев окатывание осуществляется по схемам граничного и влажного гранулирования.
В качестве связующего обычно применяют воду или водные растворы веществ, поэтому будем говорить о влаге всюду, где речь идет о связующем. Влага вводится форсунками или иными диспергирующими устройствами внутрь гранулятора. Капли, смачивая частицы порошка, способствуют соединению их либо адсорбционными силами, если влаги мало (граничное гранулирование), либо капиллярными силами и силой поверхностного натяжения (влажное гранулирование).
При всех видах окатывания механизм гранулообразо - вания на конечной стадии одинаков: внедрение частиц в гранулу при перекатывании. Но начальные стадии сухого граничного и влажного гранулирования существенно разнятся, что сказывается на скорости процесса (следовательно, производительности аппарата) и прочности гранул. При сухом гранулировании большие частицы, перекатываясь через малые, увлекают их с собой и происходит формование в соответствии с рассмотренной выше схемой. Прочность гранулы при этом определяется прочностью сил формования и связи частиц в грануле. При введении влаги зародышами гранул являются маленькие неравномерные комочки порошка, соединяющиеся вместе. Если влага только незначительно смачивает порошок, то связь между частицами в начальный период осуществляется адсорбционными слоями. Прочность гранул существенно вависит от силы адсорбционной связи.
Более сложные превращения происходят при увеличении количества влаги. Первоначально частицы соединяются жидкостными мостиками, это «канатное», или «подвешенное», состояние влаги. При окатывании уменьшаются расстояния между частицами — поры гранулы, куда выдавливается влага. Прочность гранулы на этой промежуточной стадии в основном определяется капиллярными силами. Рост гранулы за счет смачивания продолжается до тех пор, пока внутри ее вся влага не окажется заключенной в капиллярах и не будет выдавливаться наружу.
В ходе образования гранул возможны три состояния влаги [77]: промежутки между частицами содержат некоторое количество влаги; отдельные частицы связаны жидкостными мостиками; в точках соприкосновения твердое тело— жидкость — газ действует сила поверхностного натяжения в направлении распространения поверхности жидкости. В общем, это соответствует приведенной выше схеме действия влаги. Наиболее прочные гранулы были получены при применении жидкостей с большим поверхностным натяжением.
Естественно, что гидрофильность порошка способствует успешному осуществлению гранулирования. В работе [7] предлагается механизм образования гранул, в котором основное внимание уделено взаимодействию пленок влаги, покрывающих твердые частицы (граничное гранулирование): под воздействием поверхностного натяжения пленки влаги сближаются, притягивая и частицы, В дальнейшем при окатывании образуются слоистые гранулы.
Как установлено на практике, режим подачи влаги имеет существенное значение при окатывании, Непрерывная подача высокодиспергированной влаги в ту часть аппарата, куда подается исходный порошок, способствует интенсификации процесса, поскольку зародышами гранул являются частицы порошка, соединенные жидкостными мостиками. Производительность процесса является функцией количества таких зародышей.
Подачей влаги можно также регулировать размеры гранул, потому что порошок легче соединяется со смоченной поверхностью. Количество подаваемой влаги оказывает заметное влияние на конечную прочность гранул, что следует из выведенных выше зависимостей. Установлена также зависимость между скоростью роста гранул и количеством подаваемой влаги при окатывании кварцевого
песка [741. Сухой песок плохо гранулируется. При увеличении содержания влаги до 6,2% скорость образования и роста
 гранул все время растет. При дальнейшем увеличении содержания влаги гранулы начинают разрушаться от собственного веса. В зоне интенсивного образования гранул оптимальным содержанием влаги является такое, при котором поверхность гранулы является смоченной, что позволяет частицам порош-' ка налипать на нее. Г ранула при этом быстро увеличивается в размерах.
гранул все время растет. При дальнейшем увеличении содержания влаги гранулы начинают разрушаться от собственного веса. В зоне интенсивного образования гранул оптимальным содержанием влаги является такое, при котором поверхность гранулы является смоченной, что позволяет частицам порош-' ка налипать на нее. Г ранула при этом быстро увеличивается в размерах.
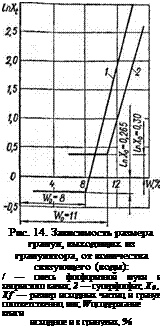
Многочисленными исследованиями установлена прямая зависимость размера получаемых гранул от содержания влаги, как это следует из приведенных выше уравнений кинетики процесса (75)—(78). На рис. 14 экспоненциальная зависимость, установленная в МИХМе, представлена графически.
 Экспериментально доказано, что применение связующего позволяет получать гранулы большего размера, чем при сухой грануляции, увеличение количества связующего также способствует увеличению размеров гранул. Так, при гранулировании песка с высоким содержанием влаги верхний предел роста гранул составлял 5—6 мм, при низком — 1—2 мм [74].
Экспериментально доказано, что применение связующего позволяет получать гранулы большего размера, чем при сухой грануляции, увеличение количества связующего также способствует увеличению размеров гранул. Так, при гранулировании песка с высоким содержанием влаги верхний предел роста гранул составлял 5—6 мм, при низком — 1—2 мм [74].
При окатывании очень сильное влияние на прочность гранул оказывает капиллярная и поверхностная влага.
Прочность сырых гранул, в первую очередь, определяется капиллярными силами [811. Жидкость, находящаяся в капилляре, в результате действия силы поверхностного
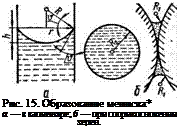
натяжения а поднимается на высоту h, которая соответствует разнице в давлении (рис. 15, а)
р = 2 a(R). (106)
Давление больше в фазе, для которой мениск является выпуклым.
Радиус искривления R зависит от радиуса капилляра г и краевого угла & между мениском и стенкой капилляра:
R = r/cosb. . (107)
Мениск может иметь поверхность, отличную от шаровой, тогда фактор 2/R выражают через (1//?! + 1 /R2), где К, и — радиусы соприкасающихся зерен (рис. 15, б) [811.
Если полое пространство сырого материала только частично заполнено жидкостью, то всасывающая сила капилляров определяется капиллярами меньшего размера. При заполнении жидкостью всего полого пространства гранулы искривленные мениски жидкости, образующиеся на выходе капилляров, оказывают всасывающее действие на жидкость, находящуюся внутри смачиваемого материала. Соответственно этому частицы (жидкие и твердые) втягиваются внутрь благодаря капиллярному всасывающему воздействию, которое вависит от величины частиц и рода упаковки. Например, при е = 26% и краевом угле © = О, т, е. минимальном радиусе искривления мениска, капиллярное давление, или капиллярное всасывающее действие,
р — 25,8а Id. (108)
Сравнивая это выражение G формулой (106), получаем d/R— — 12,9, т. е. радиус кривизны мениска почти в 13 раз меньше величины зерна.
На практике мы имеем дело как с полидисперсным порошком, так и с полидисперсным гранулятом, поэтому при расчетах под d понимаем средневзвешенную величину частиц, которые имеют ту же удельную поверхность, что и весь сырой материал. Тогда при оптимальном количестве воды капиллярное давление
P = ~l~^cosb. (109)
Из этого выражения следует, что чем плотнее упаковка, т. е. чем меньше е, тем больше капиллярное давление.
![]()
В работе [81] определено, что прочность на разрыв сырых гранул достигает значения 0,9 р, если поры внутри гранул заполнены водой:
огк«0,9 р^У~=±. (ПО)
Если в порах имеются включения воздуха, то связь осуществляется жидкостными мостиками и прочность гранул составляет только около 1/3 aZK. Сравнивая эти результаты с выводами, сделанными в работе [78], можно отметить их значительное совпадение.