ПРОЦЕССЫ ГРАНУЛИРОВАНИЯ в РОМЫШЛЕННОСТИ

ФИЗИКО-ХИМИЧЕСКИЕ основы. ПРОЦЕССОВ СТРУКТУРНОГО ГРАНУЛИРОВАНИЯ

В некоторых процессах гранулирования (окатывание, прессовое гранулирование ит. д.) исходным порошкам при­дается определенная структура в результате агломериро­вания с последующим формованием. Отсюда название этой группы процессов «структурное гранулирование». При этом промежуточной стадией процесса может быть перевод исходного порошкообразного материала в пастообразное состояние.

Ввиду сложности, многообразия и малоизученности про­цессов гранулирования единая теория гранулирования отдельных классов веществ, например порошков или паст, пока еще не разработана. В работах крупнейших исследо­вателей процессов гранулирования [72; 78; 79; 811 освещены отдельные, хоть и весьма важные стороны процессов, выве­дены закономерности, которые применимы в практической работе.

Однако все явственнее ощущается потребность в раз­работке единого подхода к процессам гранулирования оп­ределенных классов веществ. При этом могут быть исполь­зованы достижения в иных областях науки и техники — теория адгезии Б. В. Дерягина [191, современные пред­ставления молекулярной физики о взаимодействии тел, физико-химическая механика дисперсных структур, раз­работанная школой Ребиндера, представления о капилляр­но-пористых телах и т. д. Структурное гранулирование

объединяет широкую гамму процессов гранулирования, происходящих как под влиянием сил молекулярного вза­имодействия, которые являются как бы внутренне прису­щими исходным частицам, так и под влиянием сил, обуслов­ленных введением жидкости,— адсорбционных, поверхност­но-активных, капиллярных.

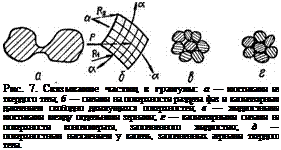
При структурном гранулировании мелкодисперсные частицы под влиянием различных сил соединяются в более крупные образования — гранулы — различными способа­ми, среди которых по аналогии с теорией адгезии Б. В. Де­рягина [19] можно выделить три основные группы:

д

1. Сухое гранулирование, которое осуществляется при отсутствии в зоне контакта частиц абсорбционных слоев и капиллярной конденсации, В этом случае частицы со­единяются в гранулы под воздействием молекулярных и электростатических сил, а также в результате непосред­ственного соединения частиц вдавливанием их друг в дру­га при формовании, В конечном счете и при формовании частицы связываются молекулярными и электростатичес­кими силами.

2. Граничное гранулирование, осуществляемое при за­зорах между частицами такой малой величины, что нахо­дящиеся в них абсорбционные слои жидкости по своим свой­ствам существенно отличаются от нее и являются основной причиной образования гранул.

3. Жидкостное (влажное) гранулирование, соответст­вующее соединению сухих частиц посредством жидкости в таких условиях, когда решающим фактором гранулообра - зования становится гидродинамика вязкой жидкости без учета природы и молекулярных взаимодействий частиц по­рошка. '

Следующие группы характерны только для процессов гранулирования:

создание мостиков из твердого тела посредством сплав­ления, химической реакции, применения вязких связую­щих веществ, способных к отверждению, кристаллизации растворенных веществ;

прессовое гранулирование, основывающееся на созда­нии определенной структуры в дисперсных системах с вы­сокой концентрацией дисперсной фазы. Эта группа процес­сов будет рассматриваться отдельно, поскольку для нее характерны закономерности, обусловленные пастообраз­ным состоянием вещества, рассматриваемые физико-хими­ческой механикой дисперсных систем.

Некоторые из этих групп представлены на рис. 7.

Сухое гранулирование. Теория межмолекулярных ван - дер-ваальсовых сил для атомов и молекул газов весьма под­робно разработана многими учеными. При сближении ато­мов волновые функции их электронных оболочек искажа­ются: в каждом атоме появляется средний наведенный ди­польный момент, причем взаимодействие этих моментов и обусловливает притяжение [19].

В полной мере эта теория применима только к разрежен­ным системам — газам. При расчетах энергии взаимодей­ствия между двумя молекулами, находящимися на рассто­янии I, может быть применена формула [78]

Еі, і — —h, i/P, (38)

где hi,/— константа, характеризующая взаимодействие, знак минус условно обозначает притяжение.

Характерной особенностью ван-дер-ваальсовых сил яв­ляется их аддитивность, т. е. энергия взаимодействия двух тел может рассматриваться как сумма энергий притяжения молекул, из которых состоят тела. Направление, развитое некоторыми учеными, позволило объяснить взаимодейст­вие макроскопических тел следующим образом. При вза­имодействии двух атомов возникает корреляция флукту­аций плотности их электронных облаков, В результате этого среднее значение флуктуационного дипольного мо­мента, прежде равное нулю (для изолированного атома), становится отличным от нуля, т. е. в каждом атоме появил­ся новый диполь.

Таким образом, исходя из положений квантовой меха­ники, ван-дер-ваальсовы силы по своей сути представ­
ляют взаимодействие дипольных моментов. Развитие этих идей привело к обоснованию макроскопической теории ван - дер-ваальсовых взаимодействий в конденсированных фа­зах, в которой ван-дер-ваальсовы силы рассматриваются как результат взаимодействий флуктуаций электромаг­нитного поля, что позволило использовать достижения мак­роскопической электродинамики и избежать предположе­ния об аддитивности ван-дер-ваальсовых сил.

На основе этих общих положений предложен ряд вави - симостей для расчета энергии и силы взаимодействия мак­роскопических тел. В работе [78] дан переход от энергии взаимодействия молекул к энергии взаимодействия кон­денсированных систем, Энергия взаимодействия элемен­тарных объемов двух сфер, содержащих в 1 м8 п молекул,

— ** Ij 2 nitijki, і, где п£ и п,- — числа молекул і и / в 1 м3,

которую в данном случае можно принять равной А — ЛВХ£,,, энергию и силу ван-дер-ваалъсовского взаимодействия между двумя шарами можно представить в виде

Е = —Ad/24l; (40)

F = Ad/24P, (41)

где d — диаметр шара.

Эти уравнения применимы лишь в пределах значений / < 0,1 мкм. Для I > 0,2 мкм действует иной экспонен­циальный закон и сила

F = Bd/m (42)

Константа В, как и константа Ван-дер-Ваальса А, зависит от свойств материала и, прежде всего, от поляризуемости и числа поляризующихся атомов или молекул на единицу объема, участвующих в переносе энергии.

В работе [78] приведены значения этих констант для кварцевого стекла. Так, установлено, что А = 10~1В Дж, В = 14 • 10-2« Дж • м.

Исходя из этих положений, было определено сопротив­ление гранул разрывающим усилиям: при I < 0,1 мкм

0г es 2 4, « 8,23 . 10-“ ^ Па; (43)

при А = 10_1в Дж I > 0,2 мкм, В= 1,4 • Ю-?8 Дж • м

7,64 . ЮгН^Па. (44)

Нетрудно убедиться, что для расстояние I > 0,2 мкм силы взаимодействия весьма малы.

Порядок полученных величин напряжений между 0,98 и 98 кПа для размеров частиц от 1 до 0,01 мкм и расстоя­ний от 1 см до 1 мм лежит в пределах значений прочности, которые можно ожидать для сухого гранулята тонкодиспер­сных частиц, например, пигментов. Верхний предел зна­чений 98 кПа практически недостижим при сухом грану­лировании.

Итак, на основании вышеприведенных расчетов можно сделать вывод, что достаточно прочные гранулы при сухом гранулировании получаются при размерах исходных час­тиц порядка 0,1—1 мкм, поскольку для частиц более круп­ных размеров влияние сил Ван-дер-Ваальса слишком мало для соединения частиц в гранулы.

Электростатические силы. В процессе гранулирования частицы приобретают электрические заряды вследствие тре­ния друг о друга и о стенки и рабочие органы аппаратов. Заряды отдельных частиц и особенно поля, возникающие вследствие этой электризации, могут существенно влиять на поведение частиц, их сближение, агломерирование. При отсутствии электрических полей силы электростатического притяжения появляются только на малых расстояниях, практически — при касании частиц.

В теории адгезии [19} используется представление о том, что при контакте твердых тел возникает микроконден­сатор и двойной электрический слой, а работа отрыва зат­рачивается на разделение пластин микроконденсатора и разрушение двойного слоя. Непосредственные измерения и косвенные расчеты на базе использования эксперимен­тальных данных определили плотность зарядов двойного слоя порядка 1/12я (0,01...0,1) Кл/м* [19]. В макроскопи­ческой картине сила взаимодействия поверхностей опреде­ляется как сила взаимодействия пластин конденсатора
на единицу площади F = 2па2, где а — плотность заряда обкладок. Такие значения заряда обеспечивают силу притя­жения порядка 9,8—98 МПа [19].

Можно рассчитать прочность связи частиц под дейст­вием сил электростатического притяжения [78]. Прини­маем, что положительно и отрицательно заряженные час­тицы ориентированы в такой же правильной последователь­ности, как и в решетке ионного кристалла. Поскольку такая высокая степень ориентированности практически недос­тижима, вычисленная сила сцепления является теорети­ческим максимумом. Считаем, что частицы имеют шарооб­разную форму и одинаковые размеры d и противополож­ные равные по величине заряды Qlt Q2, равномерно распре­деленные на поверхности частиц с плотностью ср. Расстоя­ние между частицами намного меньше их размеров: I <£ d. По закону Кулона

QiQi _. Q2 /2 /2 .

так как заряды частиц считаем сосредоточенными в их

центрах и Qj = Q2, поскольку

Q = tpwd2; (46)

F = <р2Л (47)

При ионной связи необходимо принимать во внимание вза­имодействие смежных частиц, которое количественно учи­тывает фактор ионной связи (0,2905):

F„ = 0,29 уЧЧ*. (48)

При этом прочность гранулы на разрыв

02 = 2F/d? = 2 • 0,29тгу ^ 5,8сра. (49)

Из этого можно сделать вывод, что при действии сил электростатического притяжения прочность гранулы не

зависит от ее размеров.

Различными исследователями определена плотность за­ряда на поверхности многих веществ. Например, в работе [781 для частиц пыли злаков определена плотность заряда, при которой шар из вещества плотностью р = 1 г/см8 ди­аметром 24 мкм будет поддерживаться на гладкой пластин­ке силами электростатического притяжения. Но практи­ческие наблюдения показывают, что пластина может удер­
живать частицы диаметром до 500 мкм. При этом ог2Макс =: с* 0,14 Па.

Как видно из этих вычислений, сцепление частиц, обу­словленное силами электростатического притяжения, очень мало и обеспечивает ничтожное значение напряжения гра­нул на разрыв. Следовательно, при расчетах прочности гранулята их можно не принимать во внимание.

Граничное гранулирование. Этот термин определяет группу процессов гранулирования, состоящих в связыва­нии сухих частиц адсорбированными на их поверхностях тонкими слоями жидкости.

Протекание гранулообразования при этом объясняется особыми свойствами граничных слоев [19; 30J: значитель­ным отличием концентрации молекул или ионов в слое и иной молекулярной структурой слоя на расстоянии поряд­ка 0,01 мкм от поверхности. При этом силы ионоэлектроста - тнческого характера подчиняются законам, отличающим­ся от законов притяжения Ван-дер-Ваальса, и обеспечи­вают гораздо более прочную связь частиц.

Механические свойства, в том числе и вязкость, жидкос­ти в объеме и тонком граничном слое различны. Для каж­дой жидкости характерна своя величина предельной тол­щины слоя, при уменьшении которой жидкость переходит в квазитвердое или квазикристаллическое состояние [23]. По данным работы [64] толщина такого слоя составляет для миристиновой кислоты 0,08 мкм, олеиновой—0,058мкм, высокомолекулярных ненасыщенных жирных кислот — 0,05—0,1 мкм.

Адсорбционные слои жидкости, образующиеся на по­верхности контактирующих тел, также обладают свойст­вами, отличающимися от свойств жидкости в объеме: боль­шей прочностью на сдвиг, повышенной вязкостью [23]. Вязкость граничного слоя рг в несколько раз превышает объемную Роб.

Фукс Г. И. [64] предложил безразмерный коэффициент граничного загущения для оценки изменения свойств ад­сорбционных слоев жидкости

у^ЩогР' (50)

где х0тр — время отрыва; Fотр — сила отрыва в расчете на единицу площади; р — динамическая вязкость жидкос­ти, Произведение т0Тр Аотр имеет размерность динами­ческой вязкости, а отношение его к динамической вязкос­ти в объеме отражает изменение механических свойств жид­кости в процессе разъединения тел. Сила притяжения час­тиц адсорбционными слоями [19]

F — 2 ъга. (51)

Приравняв адсорбционную прослойку к твердому веще­ству, можно количественно рассчитать прочность адсорб­ционной связи [78].

Область, для которой наиболее существенным факто­ром, определяющим прочность гранул, являются адсорб­ционные силы, занимает промежуточное положение между сухим гранулированием, где определяющими являются силы Ван-дер-Ваальса, и влажным, где гранулообразова - ние определяется капиллярными силами.

Толщина слоя жидкости на поверхности частиц, для которого существенны адсорбционные силы, составляет от 0,3 нм — толщина мономолекулярного слоя жидкости— до 3 нм, поскольку выше этого значения жидкостный слой становится подвижным [37].

Введем обозначения: а — толщина адсорбированного слоя; /„ — нижний предел влажности, считая на 1 мя объе­ма твердого вещества (о = 0,3 нм); fB — верхний предел влажности (а = 3 нм); q — коэффициент шероховатости. Тогда [78]

Сорбционные слои находятся в неподвижном состоянии до тех пор, пока толщина слоя а не превосходит некоторо­го предельного значения ак.

При этом поверхность, определяемая по формуле [781

*** * [[І + у) “ (I) ] * * у^. (55>

можсч полносгью передать когезионное напряжение окоге1,

так как

2 F I

0 2K — d2 ~ °КОГЄЗ яОк - y •

Максимальное теоретическое значение напряжения а*, достигается сцеплением сорбционных слоев на шарооб­разных частицах, касающихся друг друга (при а—0) при влажности /</в. На практике из-за шероховатостей аф 0,

Для определения Ощ по формуле (56) необходимо знать величины ак и оКогез. В данном случае принято предельное значение Ок — 3 нм.

Теоретически допускаемое когезионное напряжение превосходит 98 МПа, но его фактическую величину снижа­ют пузырьки газа, выступы и т. д., поэтому можно принять оКогез=9,8 МПа. Тогда при допускаемой прочности гра­нул на разрыв d, равной 0,1; 0,1; 1; 10 мкм, когезионная прочность сорбционных слоев Ол< составит 9,8; 0,98; 0,098; 0,0098 МПа соответственно.

Влажное гранулирование. Во всех многочисленных и широко распространенных процессах влажного гранули­рования наиболее существенным моментом является взаи­модействие жидкости и сухих частиц. При этом в зависимос­ти от количественного соотношения твердой и жидкой фаз и условий проведения процесса возможны разнообразные варианты связывания частиц в гранулы.

В точке контакта с частицами жидкость имеет вид дво­яковогнутой линзы (частицы приняты равновеликими сфе­рическими). Боковая поверхность линзы также! является вогнутой, поскольку считаем, что жидкость смачивает час­тицы, т. е. © < 90°. Кривизна поверхности линзы измеря­ется радиусами гг и г2, которые при полном смачивании зависят от радиуса частицы R и угла &.

По формуле Лапласа капиллярное давление жидкости

где К — постоянная, зависящая только от угла &. .

В случае, если жидкости мало, она распределена дис­кретными разобщенными линзами (или мостиками) в точках соприкосновения частиц. Это капиллярно разобщенное состояние, или состояние защепленной жидкости.

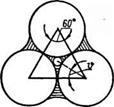
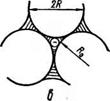
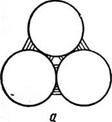
Капиллярное состояние. При увеличении количества жидкости она втягивается порами вследствие их капилляр­ности и мостики сливаются между собой. Это происходит при & = ЗСV (рис. 8). В момент слияния капиллярное дав­ление при наиболее плотной укладке ра =4,1 o/R, а содер­жание жидкости составляет 22,6% от объема пор 137]. Дан­ное состояние влаги именуется канатным.

При слиянии жидкостных мостиков создаются условия для непрерывного перехода от одной точки жидкой фазы к другой. При дальнейшем увеличении количества жидкос­ти она полностью заполняет поры, наступает так называ­емое капиллярное состояние, при котором капиллярное давление Pi=6,9ofR.

Рис. 8. Переход от стыкового состояния в канатное состояние:

а — защемленная вода: б — защемленный воздух; в —к расчету капиллярного

давления.

Если жидкость полностью обволакивает сухие частицы и ее участки сливаются на поверхности гранулы, то сила связывания частиц в этом случае определяется силой по­верхностного натяжения жидкости на границе с воздухом. Такое состояние является предельным и временным, так как жидкость будет вновь смачивать другие частицы, тем самым открывая частицы и поры, прежде скрытые ею.

В работе [78] предложено произвести расчет прочности гранул при влажном гранулировании для двух вариантой при допущении, что частицы имеют одинаковый диаметр.

1. Рассмотрим прочность связывания частиц жидкост­ными мостиками. На основании анализа размерностей ве­личина сил сцепления между частицами определяется из уравнения [78]

F ~adf (бр), (58)

где 0 — краевой угол смачивания; (3 — половина централь­ного угла жидкостного мостика. Функция /(©р) рассчитана из условий кругообразной кривизны зеркала, что справедливо при р > 10°.

При 0 = 0° (полное смачивание) и р = (10 ... 40)°

F^ (2,2... 2,7) ad. (59)

При а = 0,072 Н/м

(0,0016 ... 0,002) dH.

Как видно, изменения Р в пределах (10...40)° оказывают незначительное влияние на значение функций f и тем самым на величину F.

Введем в уравнение (58) минимальное значение F = =2,2 ad, тогда для величины сопротивления гранул на раз­рыв агв получим уравнение

(60)

Воспользовавшись уравнением (56), получим

Ozb^4,4-J. (61)

При а = 0,072 Н/м о2В й~ 32fd Па. Для d = 1 о2в 32 Па.

2. Если промежутки между частицами заполняются жид­костью, то во всем объеме действует капиллярное разре­жение, обусловленное вогнутыми поверхностями менисков жидкости в порах.

В работе [78] на основании исследований в области гра­нулирования железной руды утверждается, что прочность влажных гранул зависит от капиллярного разрежения, т. е. от поверхностного натяжения жидкости в порах. Установ­лено, что более 80% пустот большинства гранул занято жидкостью и обычно более высокая прочность гранул достигалась, когда жидкость заполняла почти весь объем пустот.

При влажном гранулировании одновременно дейст­вуют оба механизма связывания частиц в гранулы: по­средством жидкостных мостиков и капиллярного разреже­ния в порах. Независимо от формы поперечного сечения
в цилиндрических порах капиллярное разрежение при крае­вом угле © =* О

Рн = Ф, (62)

где г — гидравлический радиус (отношение поперечного сечения к периметру или объема к поверхности цилиндри­ческой поры).

При статистическом распределении частиц в грануле гидравлический радиус определяется как отношение объе­ма пустот к их поверхности:

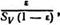(63)

где Sv — удельная поверхность гранулы, приходящаяся на объем; отсюда

Рк =

Для сферических частиц одинакового размера 5 = 6Id 1781, отсюда

Рк =

Этот расчет является весьма приближенным. Он дает лишь возможность определить среднюю высоту подъема жидкос­ти в капиллярах. На практике из-за разной величины пор жидкость в них поднимается на разную высоту. Это приво­дит к тому, что некоторые поверхностные частицы окажут­ся не включенными в жидкостный объем и будут связыва­ться друг с другом жидкостными мостиками. Однако, как увидим далее, подсчитанное на основании вышеприведен­ного расчета напряжение на разрыв и фактическое его зна­чение, определенное опытным путем, весьма близки. При этом необходимо учесть, что на области гранулы, занятые только твердым веществом, капиллярное давление не рас­пространяется и поэтому для определения предела напря­жения на разрыв необходимо выбирать только участки по­перечного сечения, занятые жидкостью.

Напряжение на разрыв, зависящее от капиллярного давления, определяется по уравнению

Оги = tpK — aSv (1 — є). (66)

В случае однородных сферических частиц напряжение на разрыв

Огк = ер* = Л. 6 (1 — є) 1 Id. (67)

Сопоставим оба теоретических механизма связи частиц при влажном гранулировании и оценим их на основании опытных данных. Отношение напряжений на разрыв для обоих механизмов связи

°гк aSv(l —„ е .

огв“ (I — t) /(2,2a - 2Ж^й-

Использовав зависимость /Се=3,1 [78], определенную эк­спериментально для различных шаров, получим

Для значений е = 0,25; 0,30; 0,40 отношение огк/о2В со­ответственно составляет 0,69; 0,82; 1,10. Отсюда можно сде­лать вывод, что при более плотных упаковках (т. е. при меньших значениях е) прочность жидкостных мостиков превосходит прочность, определяемую капиллярным раз­режением в грануле, пропитанной жидкостью. Это объяс­няется возрастанием координационного числа К при уплотнении упаковки, от которого в значительной мере зависит прочность жидкостных мостиков.

Выведенные отношения справедливы также в случае иолидисперсных частиц. При этом взамен d появляется dі — размер частиц, обеспечивающих оптимальную проч­ность. Получим выражение

J =* 3JTT2tSvdb ** °>46г <5^') №/«0. (70)

где d' — параметр тонины частиц; если частицы сфериче - кие, то оба множителя (Syd' и dhld') являются при рас­пределении функциями экспоненты л[8]. Эксперимент [78] показал высокое совпадение результатов вычислений проч­ности гранул с действительным напряжением гранул на разрыв.

Мостики из твердого тела могут образовываться при различных по своей физико-химической сущности процес­сах. При спекании, сцеплении плавлением, в результате диффузии молекул или атомов в местах микроконтактов частиц возникают мостики из оплавленного материала, ко­торые твердеют при остывании. Химическая реакция также может привести к образованию мостиков между частицами. В работе [78] описано гранулирование магнетитового

концентрата при температуре 200°С в окислительной ат­мосфере. При этом происходит окисление магнетита (Fe304) до гематита (Fe2Os), который образует мостики между час­тицами магнетита.

Связующие вещества могут отверждаться, образуя при этом твердые мостики. В зависимости от вида процесса и свойств взаимодействующих веществ связующее может вводиться в расплавленном состоянии (легкоплавкое веще­ство) либо в виде суспензии, которая при высыхании влаги скрепляет суспензированными частичками исходные час­тицы вещества. Таким способом, например, гранулируют рудную мелочь, добавляя 6—10% извести. При затверде­нии ее между частицами рудной мелочи образуются извест­ковые мостики. Кристаллизация растворенных веществ происходит при сушке влажного гранулята. Возможны две разновидности связывания частиц твердыми мостиками при кристаллизации растворенных веществ. При напылении растворов частицы соединяются кристаллами, выделившими­ся из связующего; при напылении воды на соли они частич­но растворяются и при кристаллизации соединяют сухие частицы мостиками из того же вещества. Пространства меж­ду исходными частицами, занятые жидкостью, очень малы, следовательно, будут малы и размеры кристаллов, образу­ющих мостики, определяющие прочность гранул.

Можно определить прочность гранулы, образованной вследствие кристаллизации солевых мостиков между час­тицами, условно считая, что доля объема мостиков в общем объеме вещества равна доле поперечного сечения их в об­щем сечении гранулы, что справедливо при статистичес­ком распределении:

а г ~ (71)

где гк — доля объема выкристаллизовавшегося вещества К, считая на единицу объема зерна гранулы; ак — до­пустимое напряжение на разрыв вещества К. в кристал­лическом мостике.

Для определения объема выкристаллизовавшегося ве­щества введем следующие обозначения: Y — количество растворенного вещества в процентах от массы; ft — влаж­ность перед сушкой, считая на сухое вещество, в процен­тах от массы; р — плотность гранулообразующего твердого материала; р* — плотность вещества К в кристалличес­ком мостике; е — объем пор гранулы (пористость). При этом ftp(l — е) — влажность, приходящаяся на объем гра­нулы; YkftP (1 — е) — масса растворенного вещества, при­ходящаяся на общий объем;

efc = KKf, f (1-е); (72)

Ра

1-е) о*. (73)

Ра

В табл. 3 приводятся примеры определения прочности гранул, связанных кристаллическими мостиками [781.

Таблица 3

Допустимое напряжение на разрыв вещества До* при­нято произвольно в размере 5 МПа, поскольку обоснован­ных данных для расчета не существует. Экспериментальная проверка прочности гранулы состояла в нагружении ее грузом Р. При этом отношение

о = р/тгг® (74)

дало величину прочности гранул с солевыми мостиками 120 кПа, что подтверждает правильность произведенного расчета.