ПРОЦЕССЫ ГРАНУЛИРОВАНИЯ в РОМЫШЛЕННОСТИ
ОСНОВНЫЕ ФИЗИКО-МЕХАНИЧЕСКИЕ. СВОЙСТВА ПОРОШКОВ
Под порошками понимается совокупность большого количества твердых мелкодисперсных частиц. Одним из важных свойств порошкообразных материалов является сыпучесть, т. е. способность к относительному перемещению одних частей материала относительно других. В идеальных порошках силы связи между частицами отсутствуют, что практически не встречается. В массе реального порошка между отдельными частицами всегда возникают силы воздействия, в этом случае порошок называют связным [33].
При изучении порошков необходимо всегда четко определять их состояние, чтобы получить воспроизводимые результаты.
Б
Свойство текучести (сыпучести) порошков приближает их к жидкостям. В некоторых условиях они и ведут себя как жидкости (псевдоожиженные слои). С другой стороны, порошки состоят из частиц твердых веществ, что заставляет учитывать свойства этих веществ. Кроме того, порошки обладают специфическими свойствами, не присущими ни твердым веществам, ни жидкостям.
Дисперсность. Важнейшей характеристикой порошкообразных материалов является дисперсность—распределение частиц по линейным размерам. Иначе ее называют гранулометрическим составом и определяют отношением массы определенных фракций к общей массе материала (%):
nid. lM = п; (1)
d-~ макс
£ - м, (2)
где dt — определяющий размер; md. — масса (-й фракции; М — масса материала.
Поскольку обычно порошкообразные материалы состоят из частиц неправильной формы, в качестве определяющего линейного размера принимается условный диаметр di, вычисленный по трем измерениям частиц как среднее ар ифметич еское:
4 = (3)
или среднее геометрическое:
di = V Ibh, (4)
где /, b, h — соответственно длина, ширина и высота обмеряемой частицы.
Дисперсность можно описать аналитически, а также представить в виде таблиц и графиков.
Аналитически дисперсность выражается в виде ряда распределения дискретной случайной величины d,, в котором перечисляются измеренные значения этой случайной величины dy, da, ds,..., dn с соответствующими им вероятностями ру, р2, р9,..., рп или частотами nlf п2, п8,.., пп [33]. Составить такой ряд для полидисперсных материалов весьма затруднительно, поэтому при аналитическом выра
жении дисперсности этот ряд обычно заменяют дискретным рядом классов (фракций) значений d„ При этом группа значений di, лежащая в пределах от dt М1К, до di ннн, в новом ряду представляет одно среднее значение класса:
j мако + d{ мнн
di —-------- 2------ ; (»= 1 ... «). (5)
Число классов ряда k выбирается в зависимости от количества фракций в исследуемом материале и при ситовом анализе соответствует количеству сит. .
На практике для описания гранулометрического состава (%) удобно пользоваться следующим выражением:
![]()
(m*i, т»2
м
mat
• + лГ +
ЩЛ
лг)100 =
100, (6)
где md{ ... md{... mdk — массы отдельных фракций; М — общая масса материала.
При составлении смеси из порошков с известным гранулометрическим составом можно сразу определить дисперсность смеси, пользуясь выражением
где і, /, п — различные компоненты; 1, 2, . .. , k — фракции; mdp mdr.... rn<in — массы фракций компонентов; Mi, Mj, . . . , Mr, — массы компонентов; а, Ь, ... , с— доли компонентов в смеси по массе.
Для характеристики гранулометрического состава предложены также функции счетного п (8) и массового g (б) распределения частиц [4]:
dn = п (8) d8; (8)
dt = gQL)db, (9)
где dn и dg — соответственно численная и массовая доли
|
частиц размером (SjS 4- db). Эти функции должны удовлетво-
|
Иногда в производстве гранулята важно знать, какую долю в нем составляют частицы, размер которых соответственно больше или меньше значения 6. В этом случае используются интегральные характеристики распределения по плюсу /?(б) и минусу D(б), представляющие собой процент (по массе) частиц, размер которых соответственно больше или меньше значения б [4]:
|
®мако Я (8) =100 j g(8)d8; |
(12) |
|
s D(8) = 100 f g (8) db. £MHH |
(13) |
Весьма часто дисперсность отображают в виде таблиц, особенно при исследовании смеси нескольких материалов. При этом по вертикали проставляют размеры частиц (сит), а по горизонтали — наименование материалов. Таблицы удобны тем, что позволяют быстро определять гранулометрический состав каждого компонента смеси, но для полной характеристики дисперсности нужно либо подвергать ситовому анализу смесь компонентов, либо пересчитывать данные по формуле (7), зная грансосгав отдельных компонентов.
Хорошей наглядностью обладает графическая форма отображения дисперсности порошкообразных материалов [33] (рис. 1). По оси абсцисс при этом откладывают значения размеров частиц (номера сит), а по оси ординат — соответствующий процентный состав частиц данного размера или накопленный (суммарный процентный) состав фракций. При этом в первом случае получают дифференциальную кривую распределения частиц по размерам f(di), а во втором — интегральную (кумулятивную) кривую F (di).
На дифференциальной кривой относительное содержание каждой фракции определяется площадью прямоугольника, основание которого равно интервалу значений условных диаметров данной фракции, а высота — процентному содержанию фракции, соответствующей среднему условному диаметру частиц этого класса.
По интегральной кривой распределения Можно устано-
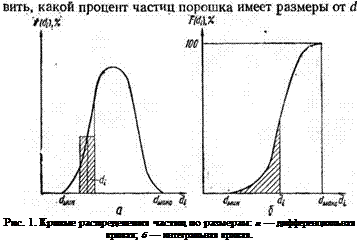 |
до d,. Численно он равен заштрихованной площади, ограниченной сверху кривой F (di), с боков — ординатами точек d„ин и di, а снизу — интервалом оси абсцисс Ad = —di d МИИі
Для расчетов гидродинамики грануляторов, процессов тепло - и массообмена и перемещения частиц нужно знать их размеры и процентное содержание в порошке. Единственным методом, дающим абсолютно точное представление о дисперсности порошка в пределах погрешности эксперимента, является непосредственное измерение размеров частиц, которое заключается в определении размеров частиц порошка под микроскопом в двух или трех плоскостях. Для облегчения анализа частицы порошка размешивают в инертной вязкой жидкости, обычно — глицерине, а затем тонкий слой образовавшейся суспензии помещают на предметное стекло. Частицы порошка имеют некоторую возможность к перемещениям, что снижает точность измерений. От этого недостатка можно избавиться, поместив
частицы порошка в полимеризукяциеся смолы. После отверждения образцы шлифуют и рассматривают под микроскопом.
Метод непосредственного измерения размеров частиц порошка применяется весьма редко, поскольку для получения достоверных данных необходимо выполнить несколько сотен, а иногда и тысяч измерений.
Наиболее распространенным методом является ситовой анализ, позволяющий достаточно быстро и с удовлетворительной для практических нужд точностью разделить порошок на фракции путем просеивания через набор сит с отверстиями разной величины. Затем фракции взвешивают.
Размеры фракций определяются наибольшим линейным размером частиц, пропускаемых или задерживаемых ситом. Через сито, имеющее отверстие а, проходит фракция — а, задерживается на нем фракция + а. Обычно обозначают верхнюю и нижнюю границы фракций либо одну из них. В различных производствах требуется различная точность измерений гранулометрического состава, т. е. практически разные наборы сит. В нашей стране действует правило, согласно которому сита обозначаются номерами, соответствующими величине размеров отверстий, выраженной в миллиметрах. Для всех сит суммарная площадь отверстий составляет 36% от общей площади сита. Такое обозначение сит позволяет сразу же получать значения фракций после выполнения анализа. Менее удобной является принятая в некоторых странах система, при которой сита характеризуются числом меш — количеством отверстий, приходящихся на I погонный дюйм (25,4 мм) сита.
В некоторых случаях, например, когда исследуются порошки с большим содержанием пылевидной фракции (/< < 0,2 мм) или требуется быстрое определение дисперсного состава, применяются другие виды дисперсионного анализа.
Широко распространен седиментационный метод, при котором используется различие скоростей осаждения твердых частиц разного размера в жидкости. Для сферических частиц диаметром d в ламинарной области скорость осаждения определяется зависимостью
№ = 0,056 (14)
где W — скорость осаждения частиц; v — вязкость жидкости; pj — плотность частиц; р — плотность жидкости.
Как видно из уравнения, скорость осаждения частиц пропорциональна квадрату их диаметра.
На практике скорость осаждения частиц иногда определяют по времени, затраченному ими с момента начала отсчета (насыпания в жидкость) до достижения контрольной отметки; однако чаще применяют более простой метод, не требующий одновременного наблюдения за многими частицами. При этом отмечают не время прохождения определенных отрезков, а вес частиц, достигших чувствительного элемента (чашечки), соединенного посредством. рычагов с регистрирующим и записывающим устройством. На этом принципе основаны так называемые седиментационные весы, с помощью которых получаем зависимость изменения массы частиц во времени G = f(т), по которой определяется грансостав.
Кроме седиментационного метода анализа дисперсности, известны также кондуктометрический, основанный на изменении сопротивления цепи при прохождении твердых частиц через микроотверстие; фотоимпульсный, заключающийся в измерении количества света, рассеиваемого отдельными частицами порошка; фильтрационный, позволяющий определить удельную поверхность частиц порошка,
« = £. Об)
где G — масса пробы; р — плотность частиц.
Представленные методы анализа дисперсности в последние годы находят все более широкое применение благодаря точности и быстроте.
Форма. Существенное влияние на протекание процесса гранулирования оказывает форма частиц, которая, как правило, зависит от свойств материала и в значительно меньшей степени — от способа получения.
Форма кристаллических частиц определяется структурой кристаллической решетки и условиями роста частиц в процессе кристаллизации. При преимущественном росте кристаллов в одном направлении образуется игольчатая форма, в двух направлениях — пластинчатая, при одновременном росте во всех направлениях—равноосная [37].
Все порошки по форме частиц можно условно разделить на равноосные, когда отношение длины к высоте и ширине не превышает 1 : 3; пластинчатые, если длина превышает
ширину, ширина значительно превышает толщину (чешуйки, пластинки); удлиненные, когда отношение длины к ширине более 3 : 1 (иголки, палочки и т. д.); овальные имеют закругленные ребра (шары, цилиндры).
Структура порошков. Важной характеристикой порошков является структура составляющих их частиц, которые могут быть как компактными, так и пористыми. При этом поры могут иметь выход на поверхность (открытая пористость) или быть замкнутыми внутри частицы (замкнутая пористость).
Структура частиц порошка в значительной степени зависит от способа его получения. Например, открытую пористость обычно имеют порошки, образующиеся в результате кристаллизации или при различных термических операциях, например при сушке, и т. д. В свободно насыпанных порошках частицы соприкасаются только отдельными участками, которые составляют ничтожную долю их суммарной поверхности — менее одной стотысячной. Кроме этих контактных участков, вся остальная поверхность порошков разделяется пустотами — порами, которые занимают в порошках от 30 до 80% объема в зависимости от формы и размеров, их шероховатости и т. д. Полидисперсные материалы, как правило, имеют меньшую пористость, чем монодисперсные, поскольку мелкие частицы заполняют промежутки между крупными, что приводит к более плотной укладке.
При влажном гранулировании большое значение имеет зазор между исходными частицами, т. е. размер пор. Если принять, что частицы имеют шарообразную форму, тогда сечение пространства между шарами будет ограничено дугами, а форма его (треугольная или четырехугольная) зависит от вида укладки частиц. При кубической укладке все поры четырехугольные, при тетраэдрической — треугольные. При других видах укладки имеются и те и другие поры в различном соотношении. В зависимости от вида укладки поры могут иметь различные размеры по отношению к диаметру сферических частиц и характеризуются величиной сферы, которую можно вписать в них: в четырехугольную пору можно вписать сферу, имеющую диаметр 0,414 d, в четырехугольную параллелограммную — 0,265d, в треугольную — 0,156 d.
Весьма интересным с точки зрения обеспечения единого подхода к процессам гранулообразования при сохранении
порошками компактности (окатывание, прессовое гранулирование и т. д.) является представление о них как о капиллярно-пористых телах. А. В. Лыков [301 предлагает под пористой средой понимать твердое тело, содержащее поры. Порошки соответствуют этому определению в том смысле, что они всегда содержат поры. Разумеется, связи между частицами порошка гораздо слабее, чем между частицами твердого тела. Если порошок находится в покое, его, несомненно, можно рассматривать как своеобразное дисперсное капиллярно-пористое тело. Т. акой подход тем более справедлив, что в качестве модельного тела при изучении капиллярно-пористых тел используют совокупность зернистых тел [30]. Тогда к порошкам можно применить многие представления физической химии о капиллярнопористых телах. В капиллярных порах действием силы тя - Рис. 2. Смачивание твердой по- жести на жидкость, находя - верхюсти.
 щуюся в них, можно пренебречь. При соприкосновении с жидкостью капилляры втягивают ее в себя, что является основой для влажного гранулирования.
щуюся в них, можно пренебречь. При соприкосновении с жидкостью капилляры втягивают ее в себя, что является основой для влажного гранулирования.
Как установлено [30], при различных видах укладки максимальная высота h капиллярного поднятия воды в сухом теле различна: при кубической укладке ft=0,205 R~1, при гексагональной — h = 0,52 R~*, для смоченного тела при кубической укладке h = 0,366 /?“ при гексагональной — h = 0,968 /?-1.
Связь с влагой. На практике очень редко приходится иметь дело с сухими порошками, обычно порошки в той или иной степени и форме содержат влагу. Порошки становятся влажными или вследствие прямого смачивания водой, или гигроскопичности. При смачивании одновременно взаимодействуют три фазы: твердая — порошок, жидкая — вода (или иная смачивающая жидкость), газообразная — обычно воздух. Смачивание протекает на границе раздела этих фаз.
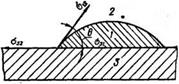
Обычно жидкость не растекается совершенно по поверхности твердого тела, при этом так называемом неполном смачивании поверхность раздела жидкости и газа пересекает твердую поверхность по некоторой линии, называе
мой периметром смачивания, и образует с ней угол в — краевой угол смачивания (рис. 2). Количественной мерой смачивания является косинус краевого угла 0, связанный с тремя поверхностными натяжениями о12, a3J и а32 трех граничащих вдоль периметра поверхностей раздела фаз: 1 — жидкость, 2 — газ, 3 — твердое тело. Поверхностное натяжение можно рассматривать либо как избыток свободной энергии, приходящийся на единицу площади поверхностного слоя: о12 == Fn/Sia Дж/м2, либо как силу, приходящуюся на единицу длины линии, ограничивающей межфазную поверхность раздела о12 = f/l Н/м. Из рисунка видно, что условием равновесия трех сил а12, а31, а32, приложенных к 1 см периметра капли воды, т. е. условием сохранения капли в состоянии покоя, будет
°3« — °S1 = °12 COS 0. (16)
Отсюда
cos 0 = °8*. (17)
°1S '
Полученное уравнение, называемое вторым законом Лапласа, определяет, что при достижении равновесия краевой угол смачивания 0 зависит только от молекулярной природы поверхностей раздела и не зависит, например, от размеров капли, что очень важно при рассмотрении смачивания порошков.
Твердая поверхность, по которой жидкость растекается, образуя равновесный краевой угол 0 < 90°, или поверхность, лучше смачиваемая водой, чем углеводородной неполярной жидкостью, называется гидрофильной, для нее а32 > а31. При 0 > 90° поверхность лучше смачивается углеводородной жидкостью, чем водой, и для нее а31 > с32. Такую поверхность называют гидрофобной или олеофильной.
Способность порошков поглощать пары воды из воздуха (гигроскопичность) оказывает заметное влияние на такие их свойства, как текучесть, способность к слеживанию и т. д. Вследствие огромной удельной поверхности порошков гигроскопичность их сказывается сильнее, чем гигроскопичность обычных тел.
Многочисленными исследованиями довольно подробно разработана теория связи влаги с твердыми материалами, в основном для целей сушки [30; 52]. Существуют три вида связи влаги с материалом: механическая, физико-химическая и химическая, различающиеся как характером и прочностью связи, так и способами удаления ее. Применительно к порошкам механическая связь характеризуется размещением капелек воды на частицах порошка или между ними.
Влага, проникающая в поры частиц вследствие адсорбции или диффузии, имеет физико-химическую связь с ними. Но из-за малого размера пор между частицами адсорбированная на их поверхности влага по форме связи также приближается к более прочной физико-химической, что, как мы увидим далее, играет огромную .роль в процессе гранулообразования. Гидратная или кристаллизационная влага образует химическую связь, наиболее прочную, ибо она состоит в связывании молекул воды молекулами твердого тела с образованием диполей. Механически связанная влага и частично физико-химическая могут быть удалены нагреванием, при этом усиливается - хаотическое движение молекул и разрушаются непрочные связи влаги с поверхностью твердых частиц. Удаляемая при нагревании влага называется свободной, а оставшаяся — гигроскопической.
Содержание влаги характеризуется несколькими величинами; основной из них является влажность W, показывающая отношение массы влаги Gh. o, имеющейся в порошке, к его массе GB:
W = Gh. o/Gb (18)
или
|
|
где Gc — масса сухого порошка.
Содержание влаги в порошке можно характеризовать влагосодержанием, которое показывает отношение влаги к массе абсолютно сухого порошка:
|
|
Влажность порошка оказывает существенное влияние на протекание процесса гранулирования. В связи с этим возникает необходимость быстрого и точного определения содержания влаги в материале.
Основным и самым надежным методом определения влажности порошка является высушивание его навески до постоянной массы. Этот метод весьма точен и прост, но требует длительного времени сушки, MHoroKpafHoro взвешивания. Кроме того, некоторые порошки разрушаются при нагревании.
К методам непосредственного определения содержащейся влаги, иногда их называют прямыми, относятся также экстракционный и карбидный 133]. Экстракционный метод заключается в извлечении влаги из порошка водопоглощающей жидкостью, в которой затем обычными методами определяется содержание влаги. При карбидном методе порошок смешивается с карбидом кальция, влага вступает в реакцию с образованием ацетилена, по объему которого определяют массу влаги.
В современной технологии все большее значение приобретают косвенные экспресс-методы определения физикохимических характеристик порошков, основанные на измерениях связанных с ними величин [33]: электрические, основанные на измерении электрофизических характеристик порошков (электропроводность, емкость и т. д.); механические, при которых о влажности судят по изменению механических характеристик порошков, зависящих от влажности (угол естественного откоса, текучесть и т. п.); ультразвуковой, при котором влажность определяется по снижению скорости распространения ультразвуковых волн; оптический, заключающийся в измерении отраженного от поверхности порошка света, и калориметрический, при котором влажность определяют по изменению теплоемкости материала в зависимости от его влажности. Некоторые из этих методов позволяют измерять влажность в потоке порошка (оптический, ультразвуковой и т. п.).
В последнее время все шире распространяются электрические методы измерения влажности, среди которых наиболее точным является емкостный, позволяющий проводить измерения с точностью до 0,5% [33]. Сущность емкостного метода состоит в измерении диэлектрической проницаемости порошков є, которая, как и для большинства капиллярно-пористых тел, не превышает 10 [30], в то время как вода имеет є =81. Между двумя коаксиальными цилиндрами — обкладками конденсатора — засыпают исследуемый материал и измеряют величину емкости.
Рассмотренная выше группа свойств порошков оказывает существенное влияние на насыпную плотность, динамические характеристики порошков и адгезию частиц порошка к стенкам аппаратов и бункеров.
Насыпная плотность часто применяется при расчетах грануляторов, ее величина является основанием для выбора размеров аппарата с целью обеспечения определенной производительности. Насыпная плотность р„ определяет массу материала М, находящуюся в единице занимаемого им объема V, поэтому иногда ее называют объемной массой:
Рн = M/V. (21)
Насыпная плотность зависит от размера частиц, их формы, шероховатости, плотности материала частиц, а также от способа укладки частиц и характера воздействия на материал. Свеженасыпанный порошок имеет одну величину насыпной плотности, подвергнутый вибрационным воздействиям или слежавшийся — иную.
При уменьшении размера частиц насыпная плотность растет до некоторых пределов, а затем вновь уменьшается. Это явление можно объяснить следующим образом. Первоначально при уменьшении частиц достигается более плотная укладка их за счет уменьшения зазоров между частицами. При дальнейшем уменьшении частиц большую роль играют силы адгезии между частицами, которые приводят к увеличению общей доли объемов зазоров (пористости), что снижает величину насыпного веса.
По величине насыпной плотности сыпучие материалы делятся на легкие (рн < 600 кг/м3), средние (600 < р„ < < 1100 кг/м3); тяжелые (1100 < р„ < 2000 кг/м8), очень тяжелые (р„ > 2000 кг/м3) [33].
Насыпную плотность иногда называют кажущейся в отличие от истинной плотности материала порошка р„. Определяют рв обычными пикнометрическими методами, поэтому ее называют также пикнометрической плотностью: в мерную емкость наливают жидкость, инертную по отношению к исследуемому порошку, и замечают ее объем 1/ж, затем засыпают порцию порошка массой М. Измерив объем образовавшейся суспензии Ис, подсчитывают истинную плотность порошка по формуле
Р„ = M/(VC - Уж). (22)
Насыпная плотность определяется разнообразными способами, основанными на измерении массы порошка, засыпанной в сосуд с известным объемом. При этом необходимо соблюдать осторожность, потому что насыпная плотность
резко изменяется при встряхивании, уплотнении порошка, например, для некоторых материалов отношение величины насыпной плотности для уплотненного и свежена- сыпанного порошка составляет 1,52 [33].
Динамические характеристики порошков. Важнейшими динамическими характеристиками порошков являются текучесть (сыпучесть), сопротивление сдвиговым усилиям, трениё порошкообразного материала по поверхности и скольжение его по наклонной плоскости. Определяются они соответственно углом естественного откоса, внутреннего трения, трения по поверхности и углом скольжения.
Текучесть. Силы взаимодействия между отдельными частицами порошка весьма слабы, поэтому они сравнительно легко перемещаются относительно друг друга подобно тому, как это происходит в жидкостях. Но в отличие от жидкостей, способных занимать любую форму без изменения объемов, порошки изменяют форму ограниченно, обычно под воздействием внешних условий. При этом изменяется, как правило, в сторону уменьшения и занимаемый ими объем.
При осуществлении процессов гранулирования к порошкам зачастую прикладываются сдвиговые усилия либо посредством рабочих органов (лопастей, шнеков и т. д.), либо поворотом массы порошка на угол, превышающий угол естественного откоса. При этом возникают силы сопротивления сыпучих материалов, обусловленные тремя группами факторов [70]. К первой группе относятся механические зацепления и заклинивание неровностей поверхностей частиц, ко второй — физические факторы: силы сцепления, адгезии, трения скольжения, трения качения, электрические и магнитные силы, третья включает физикохимические факторы: химическое взаимодействие частиц, взаимодействие окисных и абсорбированных пленок, силы поверхностного натяжения жидких добавок, в том числе капиллярные силы, обусловленные образованием менисков в порах частиц и пустотах между ними.
В порошках, состоящих в основном из равноосных, относительно крупных частиц (0,1—10 мм) с гладкой поверхностью, давление распространяется, как и в жидкостях, во все стороны равномерно [27].
В порошках металлов, состоящих из частиц неправильной ф&рмы с шероховатой поверхностью, средний размер частиц которых колеблется от нескольких микрометров до десятков микрометров, горизонтальное давление порошка на вертикальную стенку составляет 20—30% от вертикального давления на дно [6; 271. Объясняется это тем, что в порошках, состоящих из крупных гладких частиц, силы механического зацепления и заклинивания незначительны и в то же время силы трения скольжения уменьшены пленками обычно присутствующей в них воды [70]. В порошках, состоящих из малых шероховатых частиц, легко образуются рыхлые коагуляционные структуры под влиянием сил сцепления, резко увеличивающихся при уменьшении частиц.
На практике при разработке и эксплуатации грануляторов окатывания и прессовых грануляторов, успешное функционирование которых зависит именно от передачи усилий в массе порошка, очень важен учет того, в какой степени порошкообразный материал передает усилие в горизонтальном и вертикальном направлениях.
Используемые иногда для характеристики сыпучести (текучести) порошковых материалов коэффициент сыпучести /Ссып и коэффициент подвижности т определены на основании уравнения для идеально сыпучего материала, для которого величина /Ссып = const, т, е. не зависит от нормальных напряжений. Но для реальных порошков коэффициент сыпучести не является постоянным и при определенных условиях стремится к нулю, например, при увлажнении мелкодисперсного материала, состоящего из частиц неправильной формы. Учитывая это, предложено характеризовать текучесть (сыпучесть) порошкового материала величиной, определяемой отношением времени высыпания 1 кг порошка из конусообразной воронки с диаметром выпускного отверстия 15 мм и углом конусности 60° ко времени высыпания 1 кг сухого песка, который в первом приближении считают идеально сыпучим материалом.
Таким образом, эта величина, называемая относительной сыпучестью, показывает, во сколько раз сыпучесть порошкового материала меньше сыпучести абсолютно сухого песка, которая принимается за 1. Для порошка глинозема, например, относительная сыпучесть равна 5,3, известняка с размером зерен 0,5—1 мм— 1,65.
Необходимо учитывать, что понятие текучести применимо только к порошкам, у которых величина силы сцепления между частицами незначительна. Комкующиеся порошки не обладают текучестью.
Различие в углах естественного откоса для разных материалов, как это видно из рис. 3 [70], обусловлено соотношением между вертикальной N и горизонтальной G составляющими усилия F, действующего вдоль поверхности конуса. При одинаковой вертикальной нагрузке (УУ,=Л?2) усилие Flt необходимое, чтобы сдвинуть частицу вниз вдоль поверхности конуса в куче с большим углом естественного откоса (рис. 3, а), значительно больше аналогичного усилия F2 в куче с меньшим углом естественного откоса (рис. 3, б).
|
|
|
Рис. 3. Соотношение между составляющими двигающего усилия F и нормального усилии N в сыпучем материале. |
Следовательно, для разрушения свободно насыпанного порошка, имеющего большой угол естественного откоса (рис. 3, в), нужно приложить большее усилие, чем в случае меньшего (рис. 3, г).
Способность порошков к деформациям, внутреннее трение. Способность порошков «сыпаться», «течь» подобно жидкостям обусловливает своеобразие их поведения при деформациях как под действием собственного веса, так и в результате внешних воздействий. В отличие от сплошных (компактных) материалов, порошки способны как к упруго-пластическим деформациям, связанным с деформациями материала частиц, так и к структурным, связанным с относительным перемещением отдельных групп частиц относительно друг друга без деформации их материала.
Упруго-пластические деформации порошков, как и твердых тел, могут быть обратимыми, если развивающиеся напряжения не превосходят предела текучести, или необратимыми (пластические деформации или хрупкое разрушение частиц). На практике ввиду структурных особенностей порошков — малой площади контактов и пористости составляющих их частиц — основными видами упруго-пластической деформации являются необратимые пластические и хрупкие (прессовое гранулирование, таблетирование).
Структурные деформации порошков заключаются в относительных перемещениях отдельных частиц или групп и слоев частиц. Перемещения эти могут происходить как вследствие недостаточности связей у отдельных элементов (частиц) дисперсной порошкообразной системы, так и вследствие разрушения этих связей [27]. Минимальное число связей для каждой частицы порошка равно шести, а каждый контакт между частицами эквивалентен трем связям. Для шарообразных частиц наибольшее возможное число связей 12.
Структурные деформации приводят к уменьшению пористости порошка и занимаемого им объема и возникают всегда при каких-либо воздействиях на порошок; предшествуют они и упруго-пластическим деформациям. Структурные деформации необратимы и носят разрывной характер, т. е. не являются непрерывными функциями шординат'[27]. Отличие структурных деформаций от пластических состоит также в том, что одни связаны с изменением объема, а вторые могут протекать при неизменном объеме.
С приложением нагрузки или изменением положения порошкообразного тела, при котором отдельные его части начинают относительное перемещение, возникают как упругие, так и структурные деформации. Соотношение их величин зависит как от физико-механических характеристик порошков и свойств вещества порошка, так и от величины нагрузки и времени ее приложения.
В практике гранулирования порошки часто испытывают сдвиговые нагрузки, например, при прессовом гранулировании, окатывании и т. д.
При исследовании сопротивления сдвигу порошок одновременно подвергается постоянному нормальному сжимающему усилию N и сдвигающему Т, которое увеличивают до момента сдвига одной части порошка по другой.
На основании многочисленных опытов построен график, изображенный на рис. 4, характеризующий зависимость между нормальной N и сдвигающей Т силами. Кривая, отображающая эту зависимость на всем протяжении, кроме начального участка, имеет небольшую кривизну и для практических целей может быть заменена прямой (показанной на рисунке пунктиром).
 Сопротивление порошков сдвигу обусловливается внутренним трением и сцеплением частиц и описывается формулой [27]
Сопротивление порошков сдвигу обусловливается внутренним трением и сцеплением частиц и описывается формулой [27]
T = fN + cF, (23) где f — коэффициент внутреннего трения порошка, равный тангенсу угла внутреннего трения, т. е. f~ = tg ф или ф = arctg f; с — величина сцепления, т. е. сила сцепления, приходящаяся на единицу площади, по которой происходит сдвиг, Па; если силы сцепления между частицами малы, то
Т — fN. (24)
Между частицами реальных порошков, как уже указывалось выше, всегда действуют силы сцепления, которые в теории адгезии называются аутогезионными [19]. Возникновение этих сил объясняется межмолекулярными взаимодействиями, электростатическими силами, действием адсорбционных пленок, поверхностно-активных и капиллярных сил (для влажных частиц).
Частицы порошка могут быть просто зацепленными своими выступами друг за друга [27]. Величина зацепления возрастает с увеличением прочности порошка. Сила сцепления принимается равномерно распределенной по всему объему порошка, т. е. с = const. Большим сцеплением обладают мелкодисперсные влажные порошки, частицы которых имеют неправильную форму.
Внутреннее трение порошков объясняется как существованием сил трения скольжения и прилипания на поверхностях контакта частиц, так и механическим зацеплением одних частиц за другие. В общей массе порошка трение определяется не только скольжением частиц, но также их качением. Вследствие этого угол внутреннего трения порош
ка существенно отличается от угла статического сухого внешнего трения скольжения между его отдельными твердыми частицами.
 Сопротивление порошков сдвигу по указанным выше причинам зависит от плотности, влажности и размеров частиц, а также от величины перемещения. Автором работы 127] установлена стадийность протекания деформации сыпучих тел при сдвиговых нагрузках. В начальной стадии — неустановившегося сдвига — непрерывно изменяется соотношение между трением скольжения, трением качения и зацеплением. Сдвиг при этом захватывает многие слои материалов, вследствие чего область изменения пористости увеличивается при увеличении перемещения. Поэтому зависимость между сдвигающей Т и нормальной N силами на начальном участке графика носит сложный характер (см. рис. 4).
Сопротивление порошков сдвигу по указанным выше причинам зависит от плотности, влажности и размеров частиц, а также от величины перемещения. Автором работы 127] установлена стадийность протекания деформации сыпучих тел при сдвиговых нагрузках. В начальной стадии — неустановившегося сдвига — непрерывно изменяется соотношение между трением скольжения, трением качения и зацеплением. Сдвиг при этом захватывает многие слои материалов, вследствие чего область изменения пористости увеличивается при увеличении перемещения. Поэтому зависимость между сдвигающей Т и нормальной N силами на начальном участке графика носит сложный характер (см. рис. 4).
При дальнейшем действии нагрузки — в стадии установившегося сдвига — сдвиг происходит только в пределах тонкого пограничного слоя, вследствие чего изменения пористости уменьшаются. Сопротивление сдвигу при этом по какой-либо площадке достаточно точно выражается уравнением (23).
Некоторые исследователи [27] заметили аналогию между силами трения и силами внутреннего сопротивления материалов, обратив внимание на то, что внутреннее трение и сцепление сыпучего тела являются величинами того же рода, что и предел текучести или предел прочности твердого тела. Эта аналогия подтверждена экспериментально. Опыт ставился следующим образом. На поверхность песка укладывали бетонный блок, к которому прикладывалось горизонтальное усилие. По мере увеличения сдвиговых усилий непрерывно увеличивались горизонтальные перемещения, но после достижения ими определенной величины, обычно 2—3 мм, происходил срыв
блоков, после чего равномерное движение их обеспечивалось при постоянном значении сдвигающей силы.
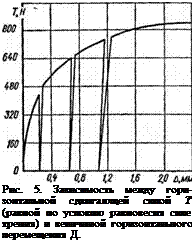
При разгрузке блок во всех случаях возвращался немного назад, как видно из рис. 5, что указывает на наличие упругих сил в общем составе сил трения.
На основании экспериментов [27] предложено для практических расчетов заменить опытную кривую зависимости между силой трения и горизонтальным взаимным перемещением трущихся тел ломаной линией, показывающей связь между перемещением А и величиной отношения силы трения к нормальной силе, т. е. величиной TIN (рис. 6).
Первый участок ломаной линии соответствует условно упругой стадии сил трения и описывается зависимостью
T/N = j*A, (25)
где [X— модуль трения, м-1, зависящий от интенсивности нормального давления на поверхность контакта.
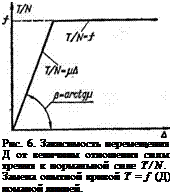 На рис. 6 модуль трения изображается тангенсом угла наклона первого участка ломаной к оси А, т. е.
На рис. 6 модуль трения изображается тангенсом угла наклона первого участка ломаной к оси А, т. е.
jj - = tg р или р = arctg (а.
(26)
При достижении некоторого предельного значения величина TIN принимается постоянной и равной коэффициенту трения /. Как и при пластической деформации твердого тела, перемещения при этом неограниченно возрастают. Практическое использование значения модуля трения и приведенной выше зависимости (25) затруднено нарушением ее линейности уже при самых малых значениях TIN.
Известна формула, выведенная на основании положений статистической механики, характеризующая возрастание угла внутреннего трения сыпучих материалов по мере увеличения плотности укладки частиц при деформации чистого изменения формы [70]:
sin 'f = 2 4- tf/v/3 * ^
где ф— угол внутреннего трения; R — число, характеризующее равномерность распределения напряжений и деформаций в сыпучем материале; f — коэффициент трения скольжения одной частицы по другой; v — отношение числа контактов скольжения к общему числу контактов, приходящихся в среднем на одну частицу.
Отношение v зависит от общего числа контактов п и для сферических частиц выражается формулой
v = 1,5—| * * (28)
Формула (27) подтверждена экспериментом [70], который показал, что угол внутреннего трения увеличивается пропорционально увеличению насыпной массы песка.
Внешнее трение. Сопротивление порошка сдвигу его по поверхности твердого тела, очевидно, подчиняется тем же закономерностям, что и внутреннее трение—сопротивление сдвигу отдельных частей порошка друг относительно друга.
Если поверхность, по которой двигается порошок, по шероховатости превосходит его, то угол внешнего трения больше угла внутреннего трения и сдвиг происходит не по этой поверхности, а по проходящей в непосредственной близости от нее поверхности внутри, сыпучего тела. Такая картина может также наблюдаться при высокой адгезии частиц порошка к твердой поверхности. На практике это встречается чрезвычайно редко. При движении плотных порошков сопротивление трения возникает как результат царапания выступающих острых краев частиц по ограждающей твердой поверхности (трение скольжения).
При движении рыхлых порошков частицы перекатываются по поверхности, изменяя свое взаимное положение, и основную роль при этом играет трение качения. Как показали эксперименты, коэффициент трения по стали рыхлых сыпучих тел меньше коэффициента трения плотных сыпучих тел, например, для грунтов нарушенного состояния это отношение составляет 2/3. Зная угол трения, по формуле (23) можно рассчитать сопротивление порошка трению. Г. К. Клейн [27] приводит таблицу, в которой величины углов трения по стали для разных материалов составляют от 15 до 55Q,
Как и для порошков, грансостав гранулята выражается процентным отношением содержания данной фракции в общей массе материала. Это один из важнейших показателей качества гранулированного продукта. В некоторых производствах к нему предъявляются жесткие требования, особенно в фармацевтической промышленности, где с размерами частиц связана величина лекарственной дозы [37].
В большинстве случаев желательно, чтобы гранулы имели примерно одинаковые размеры — монодисперсный гранулят, но поскольку получение его сопряжено с дополнительными трудностями, обычно указывают нижний и верхний пределы разбросов размеров частиц. Например, технические условия на гранулированные синтетические моющие порошки предусматривают ограничение размеров частиц до 3 мм и отсутствие в готовом продукте пылевидной фракции.
Форма гранул зависит от рода гранулируемых веществ, но в основном — от способа получения. Весьма распространены правильные формы гранул: шарообразная, овальная, дискообразная, получаемые при окатывании, гранулировании из растворов, таблетировании.
При прессовом гранулировании получают гранулы в виде цилиндров различных размеров, в кипящем слое — многогранные гранулы, при расчетах приравниваемые к шарообразным, при чешуировании — пластинчатые гранулы.
Структура гранул иногда является важнейшей характеристикой при оценке качества гранулята и решающей при выборе способа осуществления процесса гранулирования. Причем в различных производствах предъявляются совершенно различные требования к структуре гранул. Например, гранулы руды должны быть плотными и сохранять свою форму неизменной вплоть до начала плавки, а гранулы моющих средств — пористыми, чтобы облегчить доступ воды к внутренним областям гранулы и ускорить ее разрушение.
Насыпная плотность материала, как правило, увеличивается при гранулировании вследствие более плотной укладки частиц в гранулах по сравнению с укладкой их в массе порошка. Насыпная плотность гранулята более стабильна и легче поддается определению, чем насыпная плотность порошка.
Отличие динамических характеристик гранулята (текучести, сопротивления сдвиговым усилиям, угла естественного откоса и т. д.) от соответствующих характеристик порошков связано с размерами, формой и укладкой гранул, вследствие чего в массе гранулята давление распространяется во все стороны относительно равномерно. Поэтому гранулы легко пересыпаются, не слеживаются, так как у них мал угол естественного откоса, не зависают в бункерах и аппаратах. К гранулам в большей степени, чем к порошкам, применимы положения механики сыпучих тел.
Структура гранулята. (Виды и плотность укладки гранул). Для гранул неправильной формы — чешуек, пластин и т. д. — характерна хаотичная укладка частиц. Пористость гранулята в этом случае, как и для порошков, определяется формой, шероховатостью, размерами частиц и т. д.
Но для сферических гранул, получаемых распылительной сушкой, окатыванием и т. д. и довольно часто встречающихся на практике, большое значение приобретает вид укладки, от которого зависит как пористость гранулята, так и координационное число, т. е. количество точек соприкосновения частиц. Координационное число существенно влияет на физико-механические (динамические) характеристики гранулята: сыпучесть, угол естественного откоса, внутреннее трение.
Рассмотрим виды укладок сферических частиц, приняв для упрощения их одинаковыми. Многочисленными исследованиями доказано существование нестабильных видов укладки, которые при механических воздействиях переходят в более плотные стабильные виды укладки. Существуют семь нестабильных видов укладки сферических частиц, характеризующихся неправильным, беспорядочным расположением их. Как видно из табл. 1, нестабильные укладки характеризуются широким диапазоном изменения координационных чисел и соответствующих значений пористости.
|
Координационное число укладок |
3 |
4 |
5 |
7 |
8 |
9 |
II |
|
Пористость укладок, % |
77,7 |
66 |
59,7 |
43,9 |
32 |
28,7 |
28,2 |
|
Таблица 1 |
|
Характеристика нестабильных укладок |
Некоторые исследователи считают, что в общей массе часть сферических частиц всегда имеет правильную укладку, но она разделена неупорядоченной укладкой. При механических воздействиях, например, вибрировании, частицы стремятся занять более устойчивое положение, благодаря чему укладка становится правильной.
Исследования и теоретические расчеты показали, что наиболее вероятны пять типов правильной укладки: кубическая, орторомбическая или шахматная, тетрагональная или двойная шахматная, пирамидальная и тетраэдрическая, представленные в табл. 2, характеризующиеся более узким диапазоном координационных чисел и соответствующих значений пористости.
|
Таблица 2 Характеристики правильных укладок
|
Специфические свойства и характеристики гранулята. Во многих отраслях современной промышленности предъявляются высокие требования к структуре гранулята, к способности гранул разделяться под воздействием механических усилий на мелкодисперсные частицы. Это свойство можно определить термином «делимость» [78]. Особенно важна делимость гранул пигментов, добавок и наполнителей в производстве резины.
На образование гранул, обладающих хорошей делимостью, влияет как исходный материал, который должен состоять из частиц малых размеров, так и способ их получения. Гранулы должны разрушаться при определенных усилиях. Величиной этих усилий можно определить качество гранул, когда делимость является существенным требованием. В каждом конкретном случае эта величина должна быть определенной, соответствующей требованиям технологического процесса, в котором применяются гранулы.
Прочность определяет свойство гранул сопротивляться разрушающим усилиям и напряжениям, которым они могут подвергнуться при применении. Делимость гранул тесно связана с понятием прочности и соответствует допустимому верхнему пределу прочности, определяемому технологическим процессом. Нижний предел прочности гранул зависит от величины нагрузки при внутризаводских перемещениях, при складировании, расфасовке, транспортировке ит. д. К прочности гранул предъявляются повышенные требования, например, в производстве катализаторов, таблеток и т. д.
В соответствии с видом разрушающих усилий — сжатия, сдвига, разрыва — существуют понятия прочности на сжатие, сопротивление сдвигу и прочности на разрыв. Регистрацией величины нагрузки, при которой разрушается гранула, определяется прочность на сжатие. Сопротивление сдвигу отдельных гранул не играет существенной роли, поскольку, как уже излагалось выше, при сдвиговых усилиях происходит перемещение групп и отдельных частиц относительно друг друга. Определение прочности на разрыв требует проведения весьма тонкого физического эксперимента. Но именно прочность на разрыв характеризует величину силы, связывающей частицы в гранулы, и служит важнейшей физико-механической характеристикой гранул. Величина прочности гранул на разрыв позволяет определять сущность химических и физических сил, действующих при гранулировании.
Прочность определяет не только делимость гранул, она характеризует также структуру (пористость) их и может служить общей характеристикой гранулированного продукта. Кроме того, величина прочности указывает на характер сил связывания исходных частиц и помогает определить механизм гранулообразования.
Прочность гранул можно определить экспериментальным путем и рассчитать теоретически. Первый метод дает— в пределах погрешности аппаратуры — точную величину сопротивления гранулы разрушающим усилиям, второй — позволяет проверить истинность теоретических представлений о характере и величине гранулообразующих сил.
Определение прочности гранул. Поскольку для проверки теоретических представлений о гранулообразова - нии главную роль играет прочность на разрыв, позволяющая непосредственно судить о величине сил связывания,
проведен расчет допустимог о напряжения гранулы на разрыв. Необходимо отметить, что такой расчет в настоящее время может быть сделан только приближенно, поскольку отсутствуют данные, необходимые и достаточные для точного расчета.
В работе [78] выведено основное уравнение для расчета среднего теоретического напряжения гранул на разрыв, которое может выдержать поперечное сечение гранулы, при статистическом расположении гранулообразующих частиц. При этом приняты следующие допущения: число сил сцепления в поперечном сечении, находящемся под напряжением, весьма велико; статистические силы сцепления в среднем распределены равномерно (а фактически — неравномерно) по всему поперечному сечению и в пространстве; эффективные силы сцепления колеблются около некоторого среднего значения, которое может быть принято одинаковым по величине для всех участков поперечного сечения; гранулообразующие частицы являются шариками одинакового диаметра. Принимается, что поперечное сечение намного больше размеров отдельных частиц, что оно гомогенно (однородно) и во всех точках обладает одинаковой эффективной прочностью.
На практике наблюдается иная картина, например, большие'гранулы дают меньшие значения F/nra, чем малые гранулы, взятые из той же пробы. Это может быть связано с тем, что большие гранулы по своей структуре менее однородны, чем малые.
Введем следующие обозначения: ч/. — доля поперечного сечения пустот в общем сечении; k — среднее координационное число, т. е. среднее число точек соприкосновения шарика со смежными шариками; F — сила сцепления на одном участке соприкосновения, которая, согласно принятым допущениям, является средней силой и имеет определенную постоянную величину; Пр — среднее количество зерен; приходящееся на единицу поперечного сечения; XF — среднее число связей (сил сцепления) на единицу поперечного сечения; 6г — прочность на разрыв.
При статистическом распределении зерен очевидно, что Ер = е, поскольку при выполнении этого условия одно сечение ничем не отличается от другого.
Доля твердого вещества в поперечном сечении 1 — Є* =
1 1-Е
= 1 — Є И В соответствии С определением Пр = rd2,4 ■
2(1-0
![]() тЛ2! 4
тЛ2! 4
В уравнение (29) введен коэффициент к!2, поскольку каждая связь относится к двум частицам и каждой стороне поперечного сечения nd2/4 соответствует половина общего количества связей.
Здесь принято допущение, что силы сцепления статистически распределены равномерно в пространстве. Чтобы получить сумму их проекций в направлении растягивающих усилий, нужно сумму их значений помножить на частное от деления площади круга на площадь поверхности половины шара, т. е. на коэффициент 1/2. Тогда сопротивление на разрыв выразится следующими зависимостями:
oz = ±XfF, (30)
|
|
|
|
|
|
Данное уравнение позволяет определить величину сопротивления на разрыв, если известны сила сцепления каждого соприкосновения (каждой связи) и величины d, е и к, которые можно определить, исходя из дисперсности и плотности упаковки.
Объем пустот е и координационное число k — взаимно связанные величины, хотя, как было показано выше, одному значению k могут соответствовать разные величины плотности в зависимости от способа укладки частиц.
Автор работы [781 определил зависимость (1—s)k/n = = f(e) методом встряхивания сферической свинцовой дроби. Значения е = 0,26 и к = 12 соответствуют максимально плотной упаковке шаров, которая при статистическом распределении не достигается. При этом (1—г)к/п составляет 2,83. Для свободно засыпанных шаров (I—е)к/п = 1,25. Средней пористости (е ^ 0,32) соответствует значение (1 — е)к/л 2, благодаря чему существенно упрощается основное уравнение (31):
сг = 2 F/d2. (32)
Произведение ke, для максимально уплотненной (теоретической) и всех других видов упаковки, полученных
экспериментально, составляет 3,1, т. е. £е «=- 3,1 = const. Это позволяет быстро определять координационное число к при известной пористости. Произведенный расчет справедлив для гранулята, полученного из монодисперсного порошка. На практике порошки всегда полидисперсны и, следовательно, гранулы состоят из зерен разных размеров.
Выявление доли участия каждой фракции исходных мелкодисперсных частиц в суммарном сопротивлении гранулы на разрыв не представляется возможным, поскольку координационное число частицы одной фракции зависит как от общего количества фракций, так и от взаимного расположения составляющих их частиц, неизвестного нам. Вследствие этого и для расчета прочности реального гранулята, полученного из полидисперсного порошка, применим уравнение (29), употребляя в качестве диаметра d условную величину dh, соответствующую, например, средневзвешенной частице.
Тогда уравнение (31) можно записать как
приближенно можем принять его равным 2.
Рассмотрим модуль гранулы, составленной из частиц разных размеров, принимая для упрощения, что этих размеров два и dj > d2. Если в сечение попадают только однородные частицы d2, то для этих участков допускаемое напряжение на разрыв ог2 определяется уравнением (32). При попадании в сечение большого шарика напряжение на разрыв для этого участка подсчитывается с учетом площади, занятой пустотным пространством на поверхности большого шарика и силы сцепления F' в месте соприкосновения большого и малого шариков [78]:
![]() еЭ — F’
еЭ — F’
£
Для наиболее плотной упаковки шаров по расчетам, приведенным в работе [78], занятая поверхность
(I—е') = 1г/2/з;
Ой = 2,83/74 (35)
Ga = 2V2F/cP. (36)
Принимая F’ — F, получаем
Огі/Ог2 «И 1/1/6. (37)
Итак, прочность гранул, образованных из частиц разных размеров, уменьшается вследствие того, что уменьшается количество соприкосновений, т. е. координационное число малых шаров, находящихся у поверхности большого. Но если на поверхности большого шарика имеются неровности, выступы, имеющие те же размеры, что и d2, то о2 — 0,2, поскольку увеличивается координационное число малых шаров d2.