ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
АККУМУЛЯТОР, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ ФАЗОВОГО ПРЕВРАЩЕНИЯ
Рабочий цикл включает восемь периодов зарядки системы при температуре теплоносителя на входе, равной 65 °С, и четыре периода разрядки при температуре на выходе 36 °С. Эти условия обеспечивают 6 МВт ч разрядной емкости при минимальной температуре на выходе 36 °С. Регенерация теплоты при этом не ниже 70 % [39, 40].
Аналогичный принцип, по мнению авторов, может быть использован, если теплоаккумулирующий материал основан на фазовом превращении (например, парафин).
Поскольку выделяемый участок грунта имеет цилиндрическую форму, то математическая модель теплопередачи записывается в цилиндрических координатах
![]() (1.87)
(1.87)
Начальные и граничные условия следующие
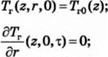 (1.88)
(1.88)
(1.89)
|
от —-(2,i?2,x) = 0; dr |
(1.90) |
|
дТ, . _ дг |
(1.91) |
|
дТ Xr-^(0,r, z) = q. дг |
(1.92) |
В этих уравнениях Тг - температура грунта, °С; 2 - глубина измерения температуры, м; аг — коэффициент температуропроводности грунта, м2/с; г - радиус спирали, м; i?2 - радиус элемента грунта, ж; т - время, с; Хг - теплопроводность грунта, Вт/(м К); q - тепловой поток, Вт/м2.
Анализ и оптимизация систем аккумулирования тепла на основе метода термоэкономической концепции впервые выполнены авторами работы [41]. Рассматривается простая схема, в которой аккумулирующей жидкостью служит вода, а теплоносителем - газ. Для загрузки аккумулятора теплом используется теплообменник в виде змеевика.
Для решения задачи термоэкономической оптимизации авторы используют метод и результаты исследований А. Бежана [42].
Генерирование энтропии Ss, кДж/К, в процессе загрузки аккумулятора за время от нуля до xs аккумулирования определяется соотношением:
|
]*}' |
Производство энтропии в процессе разгрузки в течение времени х > xs равно
Суммарное производство энтропии с учетом уравнений (1.93) и (1.94):
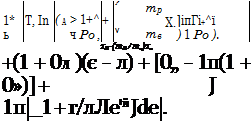 (1.95)
(1.95)
В этих уравнениях приняты обозначения: с - удельная теплоемкость жидкости (воды), кДж/(кг К); ср - удельная теплоемкость газа при постоянном давлении, кДжДкг К); М - масса жидкости в баке, кг; R — газовая постоянная, кДж(кг К); ms, mR - расход газа при загрузке и разгрузке, кг/с; р0 - атмосферное давление, кПа; ApR, Ар8 - падение давления при разгрузке и загрузке, кПа; А - площадь теплообмена со стороны газа, м2; ц - безразмерный параметр; є - параметр, характеризующий способность системы аккумулировать тепловую энергию; 0Л, 0g - безразмерная разность температур при разгрузке и зарядке; тл, тв— безразмерное время при разгрузке и зарядке; yR - параметр теплообмена.
Параметр уR определяется из уравнения:
где k - коэффициент теплопередачи, кДж/(м2 К).
|
Ь* |
Суммарный расход, дол., на содержание и эксплуатацию системы аккумулирования за год равен
В формуле (1.97) дополнительно приняты обозначения: k0 - фиксированный ежегодный взнос в систему аккумули
рования, дол. г - ежегодный внос для поддержания и эксплуатации системы аккумулирования, дол./м2', Ар - удельный расход, обусловленный необратимыми процессами, дол./(кВт ч).
Рассматривая варианты систем аккумулирования, можно определить оптимальное значение Z.
В качестве долгосрочных аккумуляторов целесообразно использовать подземное хранилище тепла. При использовании подземных аккумуляторов необходимо решить задачу тепломассопереноса в породе. Рассмотрим процесс фильтрации теплоносителя в наиболее общей постановке задачи с учетом пространственного характера и сложной структуры (неоднородности, анизотропии) пород [43, 44].
Естественные структуры скважин часто представляют собой трещиноватые или трещиновато-пористые среды. Для трещиновато-пористой породы характерно то, что основная масса жидкости не скапливается в блоках, а передвигается по трещинам. Поэтому пористость трещин и проницаемость блоков можно принять равными нулю. При таком допущении фильтрация жидкости (теплоносителя) в трещиновато-пористой среде в условиях нестационарности процесса описывается уравнением
pV(*i/VP1)+^^- = 0; (1.98)
т
дР2_+Р2~Рі =0 (І.99)
dt т
где р - коэффициент пьезопроводности, который в трещиновато-пористой среде зависит от трещин и от пористости блоков; рх и р2 - давление среды для трещин и блоков; х =ц$2/а, где р - коэффициент динамической вязкости теплоносителя; Р2 - сжимаемость пористых блоков; а - безразмерная характеристика породы, выражающая интенсивность обмена между двумя средами; t — время.
![]() Исключив из системы уравнений (1.98), (1.99) одно из давлений, получим выражение для давления в одной из сред
Исключив из системы уравнений (1.98), (1.99) одно из давлений, получим выражение для давления в одной из сред
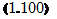 до 0V(fc, VP)
до 0V(fc, VP)
%- = PV(fyVP) + q ;• =0,
dt dt
где л = рт.
Решение уравнения (1.100) известно [31].
Приведем математическое выражение упругой фильтрации теплоносителя в геотермальной циркуляционной системе, состоящей из двух скважин: нагнетательной и эксплуатационной. В цилиндрической системе координат математическая постановка задачи имеет вид
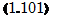
![]() d[1]U IdU 1 d2U dU _ _
d[1]U IdU 1 d2U dU _ _
—q-+—-+^5-—п-=--------- ; г>1.
dr2 г dr dr2 5ср2 SFo
tf(^<P. Fo)|Fo=0 =n(r, cp, Fo)|^M =0; Ur^ =U0; (1.102)
lim л — = g; л = Jr + ~R2 - 2rRcos (p; ч-»о drx
r=r/rc-, R = R/rc; U = (1.103)
Po
Задача решается с использованием преобразования Лапласа, методом разделения переменных и методом функции Грина. Чтобы найти решение U (г, g, Fo) используем функцию Фурье-Меллина. Получим:
где
Bn = In(x)Nn(Rx)-In(Rx)Nn(x);
Cn = In (x)Nn (rx) - In (rx)Nn (x);
Dn=I2n(x) + N2n(xy,
In (де), Nn(x) - функции Бесселя, соответственно первого и второго порядка.
Теплоперенос при установившейся фильтрации теплоносителя описывается системой уравнений:
К^г = с*Рм%, Н>г>0; (1.105)
дг дх
![]() дТ
дТ
?т “'av ~ ) = (1 ■“ ■тт )стРт “rf. 0 > 2 > - Hi
дх
|
®1т=0 *І|г|->оо 0> |
divu) = 0; 0>z>-H; (1.108)
Mk=H(wl)dTk, (1.110)
Ги
где t - температура; т - время; А, - теплопроводность; с - удельная теплоемкость; р - плотность; г — координата в направлении, нормальном к плоскости фильтрации теплоносителя; av - коэффициент теплообмена; q - плотность теплового потока; Н - мощность зоны фильтрации (диаметр скважины); т - пористость; W - массовая скорость фильтрации; Mk — массовый расход теплоносителя через k-ю скважину; Г - контур источника (стока); I - внешняя нормаль к Г; индексы *т», «ж», «k», от
носятся соответственно к породам, жидкости, нагнетательным скважинам, породам в окружающем геотермальную зону массиве.
Для скважины круглого сечения с учетом симметрии относительно плоскости г = - Н/2 будем иметь
2(1-mT)XK dtM Я~ Н дг
где q = qT + дж - тепловой поток из массива в зону фильтрации геотермальной циркуляционной системы, отнесенный к единице ее объема.
В каждом конкретном случае в зависимости от конструктивных и функциональных характеристик аккумулятора выбирается соответствующий метод решения.