Cam Mechanism Design
The variable solar day length is the result of three factors listed in decreasing order of importance: (1).The Earth’s orbit around the sun is not a perfect circle but elliptical, so the earth travels faster
when it is nearer the sun than when it is farther away; (2).The Earth’s axis is tilted to the plan containing its orbit around the sun; (3).The Earth spins at an irregular rate around its axis of rotation.
The monthly average of daylight for Brasov area is presented in Fig. 3.
|
Month
In order to determine the kinematics conditions for the tracking system, a math example is considered for the month of March when the average day time is of 12 hours. Thus, the reflector should rotate 1800 during the 12 hours (12 hours x 60 minutes = 720 minutes, average speed 150/hour). The maximization of the system efficiency is obtained by step operating the collector at specific time steps, the energy spent for collector orientation being consequently lowered.
Considering that the tracking mechanism is driven by a gear box at each 18 minutes, 40 steps per day are necessary (720min / 18 min = 40 steps). The collector should rotate 1800 in 12 hours, which means 4,5 deg/step (180° / 40 =4,5 deg/step).
Based on the above example, the control program has to guarantee 40 steps during 12 hours of daylight, every 18 minutes, to rotate the reflector by 1800. In order to transmit the movement, two opposite cams with cardioids shape are used.
In Fig. 4 there is presented the tracking mechanism for a parabolic trough collector. The mechanism driving is performed using a gear box, equipped with an control system.
Number of bolts “n” corresponding to a cam, is calculated considering the condition.
2* ж * r2
n = — = Integer no. (1)
P2
Based on these conditions, the radius r2 is chosen. If the generator radius is r2 = 600 mm (centroid corresponding to wheel with bolts) the results is n=40 bolts/cam. Thus, the tracking cam mechanism has the following dimensions:
- Centroid radia: rj =15 mm (cams centroid), r2 =600 mm (wheel centroid);
- Speed ratio: ii2=40;
- The angular step between bolts for one cam: 90.
 |
Number the sections and sub-sections. Please do not use automatic paragraph numbering.
The following steps should be achieved for the analysis of the tracking system as a multi-body system (MBS): (1) defining the mechanism as a multi-body system (bodies and geometrical constraints); (2) establishing the reference systems attached to each body (local systems for the mobile bodies plus the global system attached to the fixed body); (3) geometrical definition of the
odies on their own reference systems; (4) conversion of the coordinates from the local reference system to the global system; (5) defining the analytical equations of the global coordinates for the interesting points of the model; (6) defining the analytical equations of the geometrical and kinematical constraints; (7) formulating the differentially motion equations using different calculus formalisms (e. g. Newton-Euler, Lagrange); (8) defining the bodies mass properties and the forces/reaction torques from the tracking system; (9) solving the mixed algebraic and differentia equations system.
The analysis algorithm of the tracking system supposes the development of two specific models using MBS:
a) kinematical model - composed by the bodies connected by of kinematical joints and the geometrical parameters of the mechanism (joint placement); the input is generated using kinematical constraints (driving movements) applied in the rotational/translational joints of the driving elements which usually control the displacement and angular velocity;
b) forward dynamic model - composed by the kinematical model and the external/internal forces that act on the tracking system (e. g. mass forces, wind, etc.). The model is used to determine the driving torque (for operating with a rotational engine) or the driving force (for operating with a linear actuator) which generates the kinematical movement of the tracking system;
On the dynamic model of the system, only the inertial effect of the collector was taken into account and the wind speed was considered neglect.
The tracking system analyzed as a multi-body system method is consists of nc=3 bodies (1-fixed body, 2- cam, 3- follower).
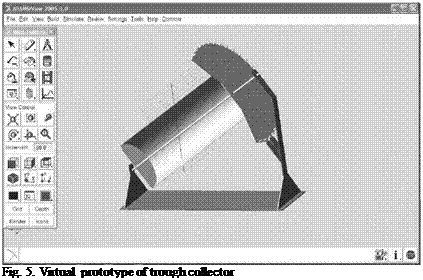 |
The degree of freedom of the mechanism, according to the structural model is M= 3*(nc-1)-Erg =3(3-1)-5=1. In Fig. 5 there is presented the virtual prototype of the tracking system mechanisms, obtained using ADAMS software.
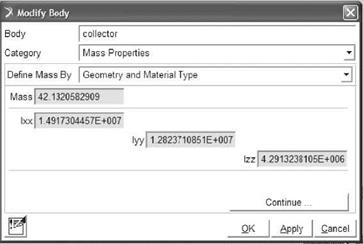
The inertial-mass properties (mass, location of mass center, inertial torques) of the tracking system bodies necessary for the dynamic model were established by means of a solid 3D modeling using Solid Works software, Fig. 4. The transfer between the CAD and MBS software (ADAMS/View) was performed using of a STEP format file (Standard for the Exchange of Product Model Data).
Using ADAMS, materials were associated for each body, the software automatically generating the inertial-mass properties of the bodies (e. g. Fig. 6 presents the properties of a parabolic trough collector). The total angle reached by the collector is 1800 (-90°...+90°), with the zero position at noon (« 12 o’clock), the return to the initial position (sunrise) being performed at 21 o’clock. Simulation is performed considering the specific conditions of the Spring Equinox (sunrise hour - 5.99 solar time, sunset hour -18.08) and the latitude of Brasov area.
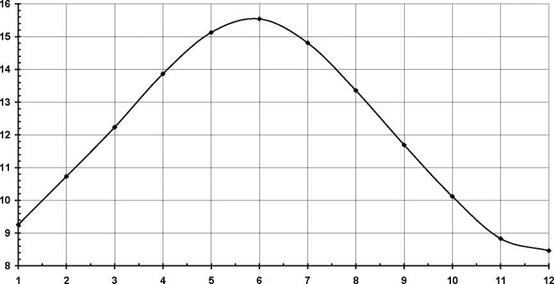
In the virtual MBS ADAMS model, the collector displacement function was modeled by summarizing a series of STEP type time functions as follows:
STEP(time, 5.99, 0.0, 8.95, 0.0) + STEP(time, 8.95, 0.0, 9.05, 15.0d) + STEP(time, 9.95, 0.0, 10.05, 15.0d) + STEP(time, 10.95, 0.0, 11.05, 15.0d) + STEP(time, 11.95, 0.0, 12.05, 15.0d) + STEP(time, 12.95, 0.0, 13.05, 15.0d) + STEP(time, 13.95, 0.0, 14.05, 15.0d) + STEP(time, 14.95,
0. 0, 15.05, 15.0d) +STEP(time, 15.95, 0.0, 16.05, 15.0d) + STEP(time, 16.95, 0.0, 17.05, 15.0d) + STEP(time, 17.95, 0.0, 18.05, 15.0d) + STEP(time, 21.0, 0.0d, 21.2, -180.0d).
With these values, the collector displacement function is presented in Fig. 7.
|
Fig. 6 Inertial-mass properties of the trough collector |
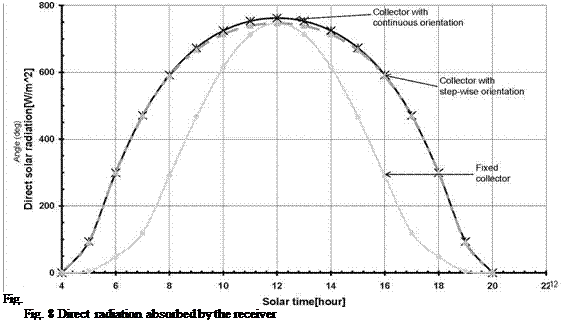
In order to evaluate the tracking system efficiency, the amount of direct radiation which reaches the receiver was calculated, using literature equations correlating the sun movement on the sky and the collector rotational angle [5, 11, 12, 13].
In Fig. 8 the diagrams obtained for the radiation collected on the trough receiver are presented for the following cases: (1) the trough collector is continuously orientated; (2) the trough collector is rotated using the displacement function as presented in Fig. 7; (3) the trough collector is fixed being orientated South.
As Fig. 8 shows, the step - wise tracking proposed leads to efficiency almost equal, (98%) with those obtained by continuously tracking.
The efficiency increase due to tracking is over 35%.
Tacking step - wise mechanisms based on double cams and multiple followers are presented as a solution for parabolic trough collector. In comparison with other tracking systems, this system presents the following advantages:
- perform high gear transmission ratio and efficiency having reduced dimensions;
- the continuous rotational movement from the double cam to the bolts wheel is performed (the two cams gear on the same time with the opposite rollers for a cam rotation of ф2=180°...254°);
- high loading capacity due to a high contact ratio;
- low costs due to a simple design;
-
 |
simple maintenance.
Based on the dynamic model, the torque required for the collector orientation was obtained. The collector daily motion was performed in steps, the displacement function being established considering a minimum number of actions. By using this tracking system the amount of direct radiation captured by the parabolic trough receiver raises with about 35% than in the case of fix collectors orientated toward to the South.
The designed tracking system achieves the imposed movement functions and meets the desired placement of the collector along the operating cycle. Starting from this virtual prototype both the mechanism and the tracking algorithm will be tested in laboratory and field operating conditions. Based on the tests, the tracking algorithm is optimized targeting a minimum number of steps thus, an increased overall energy efficiency.
[1] http://www. powerfromthesun. net/chapter1/Chapter1.htm.
[2] http://www. solarpaces. org/csp_technology. htm.
[3] Ciobanu, D., Visa, I., Tracking systems for parabolic trough collectors, Bulletin of the Transilvania University of Brasov, vol. 12-series A, ISSN 1223-9631, Brasov, 2005, pg. 29-36.
[4] Ciobanu, D., VISA., I., Tracking system type cam mechanisms for parabolic trough collector, Acta Techica Napocensis, vol. II (50), ISSN 1221-5872,auj Napoca, 2007, pg. 115-120.
[5] Duffie, J. A., Beckman, W. A., Solar engineering of thermal processes, Second edition, A Wiley - Interscience Publication, John Wiley & Sons, 1991, ISBN 0-471-51056-4.
[6] ***The World Patent No: WO 0310 1471A.
[7] ***The US Patent No: US 446938.
[8] *** The Russian Patent No: 2105935.
[9] ***The US Patent No: US 5798517.
[10] Dudifa, Fl., §.a.,., Mechanisms course. Gear pairs. Cam mechanisms. Kinematics, Transilvania University of Bra§ov, 1989.
[11] Burduhos B., Visa I., Rusu C., Diaconescu D.: On the Orientation Cycle Optimization of a PV Testing Tracked Platform, CSE 2008 - 2nd Conference on Sustainable Energy, Brasov, Romania, 3-5 Iulie 2008, ISBN: 978-973-598-316-1, pg. 85-92.
[12] Diaconescu, D., Visa, I., Burduhos, B., Saulescu, R., Orientation data needed in the design of the pseudo-equatorial tracker’s control program, OPTIM 2008-11* International Conference on Optimization of Electrical and Electronic Equipment, Basov,2008, Romania, ISBN 978-973-131-030-5, pg. 449-454.
[13] Diaconescu, D., Visa, I., Burduhos, B.: On the Received Direct Solar Radiance of the PV Panel Orientated by Pseudoequatorial Tracker, COMEC - The 2nd International Conference Computational Mechanics and Virtual Engineering2, Brasov, Romania, 11 - 13 Octombrie 2007, ISBN 978-973-598-1174, pg. 43-48.