ЧТО МОЖЕТ ВИБРАЦИЯ?

ВИБРАЦИЯ ГАСИТ ВИБРАЦИЮ — ВИБРАЦИЯ УСИЛИВАЕТ ВИБРАЦИЮ (ОБОБЩЕННЫЙ ПРИНЦИП АВТОБАЛАНСНРОВКІІ)

13.2. Обобщенный принцип автобалапспровкп

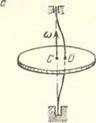
Еще в 1884 г. шведский инженер Лаваль обнаружил, что неуравновешенный диск, сидящий на гибком валу, в закритической области частот вращения, т. о. при ча­стотах ©, значительно больших частоты свободных коле­баний р, самоцентрируется: его центр масс располагается практически на оси вращения (рис. 14.1, а). В итого существенно снижаются неуравиовешеппые усилия, пе­редаваемые па опоры вала. Этот эффект, впервые теоре­тически объясненный в 1895 г. Фёпплем [220], успешно используется при создании различного рода машин с быстро вращающимися роторами, папример центрифуг. Он проявляется и в других, в том числе более сложных роторных системах (рис. 14.1,6 и в), что также находит важные применения (см., папример, изобретения [203, 204], позволившие существенно усовершенствовать маши­ны для стирки белья).

Из изложенного в п. 12.3.3 и 12.4 интегрального при - зпака (экстремального свойства) устойчивости синхрон­ных движений механических дебалансных вибровозбуди­телей — неуравновешенных роторов, приводимых от дви­гателей асинхронного типа,— вытекает ряд практически важных следствий, которые можно рассматривать как су­щественное обобщение закономерности, обнаруженной Лавалем. Напомним, что согласно этому критерию устой­чивые синхронные движения некоторого числа к роторов с одинаковыми положительными парциальными угловыми скоростями [27]) обладают тем замечательным свойством, что им соответствуют грубые минимумы[28]) среднего за период значения функции Лагранжа L(I) = Та) — П11), вычисленного для колебательной части системы, на ко­торой установлены роторы, и в предположении, что ро­торы равпомерно вращаются по закону

ф, = а3(мі + а„) (а, = ±1; s=l, ..., к), (14.1)

л колебательная система (несущие тела) совершает уста­новившиеся колебания под действием неуравновешенных сил, развиваемых роторами в указанном движении. Из условия минимума выражения

D -= <(L(I>)> = <(Г(1) - П(1,)> (14.2)

— так называемой потенциальной функцпп — определя­ются пачальные фазы alt..., ак в устойчивых синхрон­ных движениях (точнее — разности этих фаз а( — оск, ...

.., a*-i-aA).

Если теперь учесть, что в закритической области ча­стот © > pmaz {ртлг — наибольшая частота свободных ко­лебаний системы при заторможенных роторах; мы рас­сматриваем здесь системы с конечным числом степеней свободы) потенциальной энергией можно пренебречь по сравнению с кинетической, то получается первое важное обобщение обнаруженной Лавалем закономерности на мпогороторные системы: в закритической области частот роторы с одинаковыми положительными парциальными угловыми скоростями самоуравновешиваются в том смыс­ле:, что средняя кинетическая энергия колебательной ча­сти системы имеет минимум; если при этом возможна такая фазировка роторов, при которой несущие тела не­подвижны, т. е. Т{1) = 0, то эта фазировка непременно будет устойчивой. Такую фазировку назовем компен­сирующей.

Сказанное иллюстрируется рисунками 12.6, е; 12.7, а; 12.8, а и 14.1, д и и, 1.

Другая важная закономерность, вытекающая из инте­грального критерия, состоит в том, что весь диапазон частот вращения 0 < ю < 00 разбивается на интервалы, разделенные частотами свободных колебаний системы

РI = Pmtn, . . Pn — Pms. г II ПвКОТОрЫМИ ДРУГИМИ ЧЭСТОТаМИ

<7ь..., </г, в которых поочередно имеет место то само - уравновешивание, то усиление колебаний. При этом в закритической области и > pmil} как отмечалось, не­пременно имеет место самоуравновешивание, а в области м < рmm — усиление колебаний (в последнем случае мож­но считать, что Т11) < П(1), так что устойчивым движе­ниям отвечает максимум потенциальной энергии). Эта закономерность иллюстрируется рис. 14.1,3 и и, 1.

Выше для упрощения рассуждений мы говорили о роторах с одинаковыми парциальными угловыми ско­ростями. Для роторов, парциальные скорости вращения которых несколько отличаются, сформулированные зако-

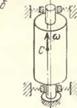
Рис. 14.1, а, 6, в, г, Q, е, ж, з. Обобщенный принцип автобалансировки неуравновешенных вращающихся тел: а) классическая система; центр масс статически неуравновешенного диска, вращающегося на невесомом упругом валу, в закритической области частот вращения со > р неогра­ниченно приближается при к оси вращения; б) то же характерно

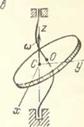
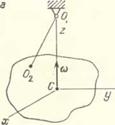
для жесткого статически неуравновешенного ротора, вращающегося ь упругих опорах; в) главная центральная ось инерции Cz статически и динамически неуравновешенного диска, вращающегося на невесомом уп­ругом валу, при со > р неограниченно приближается при ю^оо к оси вра­щения; г) одна из главных центральных осей инерции твердого тела, вращающегося на струнном подвесе, при ю-»оо приближается к вертика­ли, проходящей через точку подвеса (V, д) два одинаковых неуравнове­шенных ротора, установленных на невесомой упругой балке, взаимно уравновешиваются в закритической области частот вращения со > р;

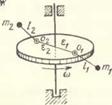
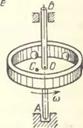
е) в той же области нормально работает автобалансир, установленный на невесомом валу: шарики 1 располагаются в полости диска 2 таким образом, чтобы компенсировать его статическую неуравновешенность;

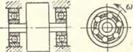
ж) так же ведут себя маятники J, закрепленные на диске 2, вращающем­ся на невесомом упругом валу; з) сепараторы подшипников качения, в которых установлен жесткий ротор, при синхронизации в закритиче­ской области частот вращаются так, что происходит взаимная компен­сация колебаний вала, вызываемых некоторыми погрешностями изготов­ления Подшипников
номерности сохраняются в виде некоторой тенденции. Та же тенденция к взаимной компенсации неуравновешен­ностей в закритической области частот вращения была обнаружена для ротора с маятниковыми подвесками

1)

- +

Рис. 14.1, и, к. Обобщенный принцип автобалансировки неуравновешен­ных вращающихся тел: и) одинаковые неуравновешенные роторы, уста­новленные на упруго опертом твердом теле, при устойчивом синхронном вращении в закритической области частот (а > Ртах взаимно компенси­руют вызываемые ими (J) или внешней гармонической силой (2) коле­бания тела, которое остается практически неподвижным; при ю < pi име­ет место максимальное усиление колебаний, а диапазон pi < ю <Рщах распадается на промежутки, в которых поочередно происходит компенса­ция или усиление колебаний; аналогичная картина имеет место в слу­чаях, когда упругие валы и балка на рис. д) — ж) обладают распреде­ленной массой, т. е. когда ртах “00 (знаком «—» помечено взаимное расположение роторов при компенсации, а знаком « + » —при усилении колебаний тела; так же помечены соответствующие промежутки измене­ния (о (3); к)—еще более сложная система — жидкость, частично за­полняющая сосуд, вращающийся на упругом валу,— может образовать в зависимости от значения частоты вращения <о, как предельно уравнове­шенную (—), так и предельно неуравновешенную ( + ) конфигурацию

(рис. 14.1, ж), автобалансиров (рпс. 14.1, е; см. также п. 14.2.2) и некоторых других роторных систем, в част­ности для таких своеобразных роторов, которые пред­ставляют собой сепараторы подшипников качения, уста­новленных в опорах некоторого вида (рис. 14.1, з) [1, 42, 94]. Как установлено, при самосинхронизации

в закритической области сепараторы обнаруживают тен­денцию к взаимной компенсации вызываемых ими коле­баний вала в опорах. Особенность этого случая состоит в том, что здесь колебания вызываются не неуравнове­шенностью сепараторов, а неточностями изготовления подшипников, вследствие которых потенциальная энер­гия колебапий системы зависит от углов поворота сепа­раторов[29]) [94].

Блпзкие по характеру закономерности были обнару­жены А. Ю. Ишлинским и его учениками и коллегами в поведении иной, как оказалось, достаточно сложной системы — твердого тела, вращающегося на струнном подвесе (рис. 14.1, г) (см. статью и книгу [105, 107], а также работу [193], где прпведепы библиографические ссылки).

Таким образом, сразу несколько видов устройств с вращающимися роторами, вызывающими колебания си­стемы, на которой они установлены, обнаруживают об­щую закономерность поведения, которую можно рас­сматривать как некоторый обобщенный принцип автоба­лансировки и сформулировать следующим образом.

Отдельные роторы или несколько синхронно вращаю­щихся роторов, установленных в единой колебательной системе и вызывающие ее колебания вследствие неурав­новешенности или других факторов, обнаруживают в об­ласти частот вращения выше наибольшей частоты сво­бодных колебаний системы тенденцию к ослаблению ко­лебаний, в области ниже наименьшей частоты свободных колебаний — к усилению колебаний системы, а промежу­точный диапазон частот вращения распадается на про­межутки, в которых поочередно имеет место тенденция то к самоуравновешиванию, то к усилению колебаний.

Выше речь шла о поведении роторов в колебательных системах с конечным числом степеней свободы. Исследо­вания показывают (см., например, [90, 35, 42]), что ска­занное о перемежаемости диапазонов самоуравновепшва - пия н усиления колебаний распространяется также на случай, когда упругие валы и балка на рис. 14.1, д— ж обладают распределенной массой (в этих случаях pmzz =■ *=■«>). Аналогичное поведение, по крайней мере при не слишком высоких частотах вращения, обнаруживает п

еще пе лостаточпо полпо изученная система с ротором, содержащим жидкость (рис. 14.1, к); это обстоятельство использовано, в частности, в изобретении [38].

Другое обобщение отпосится к случаю, когда роторы связаны также пекоторой системой так называемых не­сомых связей. Одпако на соответствующих результатах, базирующихся на исследованиях Р. Ф. Нагаева [155], мы здесь не останавливаемся.

Отметим, что в пределах каждого пз рассмотренных выше типов систем сформулнрованпое положение пред­ставляет собой достаточно строго теоретически установ­ленный и экспериментально проверенный факт. Однако общего доказательства этого положения, охватывающего все разнообразные роторные системы, о которых шла речь, еще не существует. Поэтому указанное положение отпесено нами к разряду припципов.