О поведении сыпучей среды в вибрирующих сосудах
Случай сообщающихся сосудов
Поведение слоя сыпучей среды в вибрирующих сосудах. а также закономерности распространения вибрации в толщу сыпучей среды представляют значительный интерес для впбрационпой техники и технологии. К сожалению, эта задача механики в настоящее время еще далека от удовлетворительного решения. Здесь мы остановимся лишь на описании некоторых основных примечательных закономерностей п сошлемся па имеющуюся литературу.
Некоторое определенное распределение вибраций в сыпучей среде (включающее детерминированную в среднем и случайную компоненты) устанавливается в ней достаточно быстро — после истечения нескольких периодов колебаний. Это «быстрый» процесс, на фоне которого затем разворачиваются медленно протекающие процессы — возникают определенные потоки, происходят процессы сегрегации (самосортпроваипя). Ряд таких процессов рассмотрен в разделах 4, 7, 8, 11. Естественно, что для изучения этих медленных (видимых наблюдателем V) процессов знание быстрого процесса, т. е, установившегося вибрационного поля, представляет первостепенное значение. При ускорениях Лео2<g для вертикальных и /1ш2</,£ для горизонтальных колебаний (/( — коэффициент трепня покоя) материал движется в основном вместе с сосудом. При ускорениях Ло)2»£ частицы материала приобретают некоторую взаимную подвиж - пость — начинается его псевдоожижеиие, приводящее сначала к уплотнению, а затем — при дальнейшем увеличении Л (о2 — к разрыхлению и перемешиванию (см. разделы 7—9). Процессы разделения (сегрегации, самосор - тировашш) происходят в стадиях нсовдоожижения и разрыхления.
Лишь при сравнительно небольшой толщине слоя (не более 20—30 среднего размера частиц) и не слишком интенсивной вибрации (Лш2=^10£, 20 с-1 < со < 300 с-1) допустимо считать, что слой колеблется как единое целое, и его движение можно рассматривать как движение материальной точки. D более толстых слоях колебания частиц постепенно затухают по мере удаления от вибрирующих поверхностей [165, 207, 231]; для их описания предложен ряд дискретных и непрерывных моделей.
Дискретные модели «набирают» из элементов в виде сосредоточенных масс, демпферов сухого и вязкого трепия и элементов, имитирующих неудерживающпе связи [30; 61, т. 4; 73, 74, 132, 207]. В качестве моделей с распределенными параметрами иред - лагались уируговязкне, вязкоупругие и упругоплаетпческне тела [61, т. 4; 205, 240]; иная — виброреологическая модель предлагается в п, 6.6. Изящно и до конца решается задача о движении слоя сыпучей среды в широком сосуде с горизоптальпым дпоч, совершающем круговые горизонтальные колебапия; при этом предполагается, что коэффициент сухого трепня внутри слоя несколь
ко увеличивается по мере роста нормального давлепия [78, 791. Заслуживают впимапия концепция вибропроводпости |" 167, 168], когда процесс распространения вибрации в среде полагается аналогичным распространению тепла, а также попытки использования методов физической кинетики [186].
В связи со сказаппым отметим, что при построении и оценке виброреологических моделей особенно существенны общие положения о математическом моделировании в механике, высказанные в работах [201, 202]; ряд соображений по отому поводу содержится также в книго [44].
Как показывает эксперимент, важным фактором, влияющим на поведение сыпучей среды в вибрирующих сосудах при интенсивности вертикальной вибрации Лш2 > g, т. о. при движениях с отрывом, является сопротивление воздуха (его фильтрация сквозь слой частиц) [236, 241, 242]. Если отдельная крупная частица или достаточно тонкий слой крупных частиц материала может находиться при Л со2 > 3,7g в состоянии отрыва от дна сосуда в течение промежутков времени, больших периода колебаний Т = 2л/со, то для достаточпо толстого слоя эти промежутки пе превышают периода колебаний. Перепады давлепия воздуха на высоте слоя материала могут на порядок превосходить атмосферное давление.
|
|
|
5 в |
|
г |
|
д в |
|
|
|
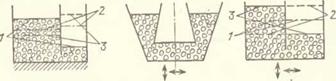
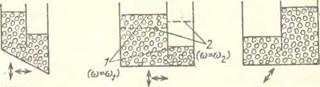
Рис. 6.6. В отличие от жидкости, в сообщающихся сосудах с сыпучей средой при асимметрии системы или вибрации устанавливаются различные уровни свободной поверхности: а) неподвижные сосуды — возможно бесконечное число положений равновесия среды (например, положения 1, 2, з); б) симметричная вибрация симметричной системы — «нормальный» случай; в) симметричная вибрация симметричной системы— особый случай (состояние 1 при одинаковых уровнях неустойчиво или устойчиво при малых возмущениях; в зависимости от начальных условий могут устанавливаться состояния 2 или з); г) симметричная вибрация сосудов со скошенным дном; 9) симметричная вибрация сосудов с различными площадями поперечных сечений (при различных частотах могут устанавливаться различные состояния 1 или 2); е) асимметричная вибрация симметричной системы (вибробуш. еризация) |
|
причем в двух взаимно симметричных состояпиях 2 и 3 уровни различны. Это связано с неустойчивостью (нли устойчивостью лишь при достаточно малых возмущениях) состояния 1 с одинаковыми уровнями. Какое из двух (или трех) состояний 1—3 установится в действительности, зависит от пачальпых условий движения (о возможности такой ситуации говорилось в подразделе 4.2 (см. рис. 4.1, а, VI). Что касается случая, представленного на рпс. 6.6, е, то он соответствует эффекту вибробун - керизации, рассмотренному в п. 4.3.2. Заметим, что существенная для приложений величина перепада уровней зависит как от геометрических параметров системы, в том числе от размеров переходных элементов, так и от параметров вибрации. Отметим также, что каждое из уст- |
Принципиальный п прикладной интерес представляет поведение сыпучей среды в сообщающихся вибрирующих сосудах (рнс. 6.6); оно типично для систем с сухим трением. При отсутствии вибрации возможно бескопеч - иое число непрерывно распределенных положений равновесия определенного объема материала в сосудах —положений, соответствующих различным уровпям свободной поверхности среды в сосудах (рис. 6.6, а). В случае полной симметрии системы —при одинаковости сосудов и симметричности вибрации относительно вертикали, например при строго горизонтальных или строго вертикальных грамопических колебаниях (рис. 6.5,6),— как правило (но пе всегда, см. ниже), в квазнравновесном состоянии устанавливаются одинаковые уровни среды. В случае неодинаковости сосудов (рис. 6.6, г и д) или асимметрии вибрации (рис. 6.6, е) квазиравновесные уровни будут различными. Модель ситуации, соответствующей рис. 6.6, г, была теоретически и экспериментально изучена М. И. Лпиовским [61, т. 4], показавшим, что в данном случае важную роль играет паличне воздушной среды (в условиях вакуума уровни оказывались одинаковыми), н предложившим ряд оригинальных устройств. Модель, отвечающая рис. 6.6, д, предложена и изучена в работе [125]; об использовании соответствующего эффекта, обнаруженного В. Ф. Палпловым, говорилось в п. 4.3.2 (см. рис. 4.9). Примечательно, что, как было установлено экспериментально и объяснено теоре-
тическп, в этом случае при различпых частотах вибрация более высокий уровень среды может установиться в различных сосудах. Еще более любопытно, что при определенных условиях в совершенно симметричной системе и при симметричной вибрации в сосудах могут установиться два пли даже три различных состояния (рпс. 6.6, в),
ройств, изображенных па рис. 6.6, а, в—е, может быть использовано как вибротранспортирующое, если обеспечить удаление сыпучей среды из зоны вблизи папболсе высокого уровня устанавливающейся свободной поверхности.
Описаппые эффекты убедительно свидетельствуют о том, что вибрация не просто приводит к псовдоожшкепию сыпучей среды, но вызывает также появление вибрационных сил. С позиции наблюдателя V именно эти силы приводят к несправедливости в данном случае закона сообщающихся сосудов для жидкостей. Не справедливо в данном случае и утверждение, что положения устойчивого равновесия системы соответствуют минимуму потенциальной энергии силы тяжести: при различных уровнях среды в сообщающихся сосудах центр масс располагается выше, чем при одинаковых. (Об ошибочности так называемой потенциальной теории по отношению к изучаемым системам см. также раздел 7 и рис. 7.3.)