Эффективные коэффициенты сухого трения при вибрации. Вибрационная концепция трения скольжепня, квазнпластическнй удар
При действии па системы с сухим трением вибрации относительно малой интенсивности еще не происходит кажущегося изменения вида трения, а «изменяются» лишь основные характеристики — коэффициенты сухого трения. Этот эффект представляет собой простейшее проявление виброреологических закономерностей, допускающих элементарное рассмотрение [26, 30].
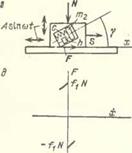
Рассмотрим сначала тело, которое прижато к шероховатой плоскости силой N и на которое действует сила S, направленная вдоль плоскости (рис. 6.2, а). Пусть на тело действует также продольная гармоппческая сила *J> = <I>0sina>i; тогда, для того чтобы тело начало двигаться вдоль плоскости, необходима не сила S = = ffl,
|
|
|
fu± m Tt+ "- |
|
|
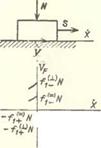
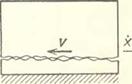
Рис. в.2. Эффективные коэффициенты сухого трения: а) тело на неподвижной шероховатой плоскости под действием гармонически изменяющейся силы; б) тело на гармонически колеблющейся шероховатой плоскости (7, в, і — случаи продольной, поперечной и иродолыш-понеречний силы или колебаний плоскости); в) наблюдателю V представляется, что коэффициент сухого трения уменьшается; в) тело с «внутренней степенью свободы* на гармонически колеблющейся шероховатой плоскости;
в) наблюдателю V представляется, что коэффициент сухого трения уменьшается и различен при смещениях в ранличны! направлениях; е) зависимости эффекгивных коэффициентов от частоты колебаний
как прп отсутствии силы Ф, а лишь сила S(=*’ = }{N — Ф0 (ft — коэффициент трения покоя). Поэтому наблюдателю V, «не видящему» быстрой силы Ф (рис. 6.2, в), будет казаться, что коэффициент трения покоя по отношению к медленной силе 5 уменьшился, приняв значение
Аналогично при действии силы Ф перпендикулярно плоскости
Г = л(1-£). (6.2)
Если сила Ф параллельна плоскости п паправлепа перпендикулярно силе S, т. е. плоскости рисунка, то
А’-А/і-($)’• (6.3)
Введем параметр
w = <£JN, (6.4)
характеризующий относительную интенсивность вибрации и называемый параметром перегрузки или просто перегрузкой. Тогда формулы (6.1) — (6.3) запишутся в виде
Л-> = А (і - f} Аи = А (і - »). Л" = и j/1 - Щ‘-
Формулы (6.5) остаются справедливыми в случае, когда сила Ф отсутствует, но плоскость совершает гармонические колебания в соответствующих направлениях
(рпс. 6.2, б); прп этом следует лишь вычислять параметр перегрузки по формуле
w = mA(i)l/N, (6.6)
т. е. положить в (6.4) Фа — mAaf, где m — масса тела,
А — амплитуда, а w, как и ранее,— частота вибрации.
Наконец, если нормальная сила N представляет собой вес тела mg, то
w = Aa>i/g. (6.7)
Формулы (6.1) — (6.3) и (6.5) имеют смысл до тех
пор, пока величины А А±у и fi названные эффек-
79
тивными коэффициентами трения при вибрации, положительны; при больших значеннях параметра перегрузки w происходит уже кажущееся изменение характера трения; в этом случае следует считать, что эффективные коэффициенты трения равны нулю.
Более сложный и интересный результат получается, если тело, находящееся на вибрирующей шероховатой плоскости, обладает «внутренней степенью свободы», т. е. с ним посредством упругого элемента жесткости с и демпфирующего элемента с коэффициентом вязкого сопротивления h связано некоторое тело массой mt (рис. 6.2,г); пусть это дополнительное тело может перемещаться относительно основного тела вдоль некоторого фиксированного направления, образующего угол к с его основанием. Как показывает несложное исследование, аналогичное проведенному выше [34], в рассматриваемом случае вследствие конструктивной асимметрии системы (см. п. 4.2 и рис. 4.1, а, III), имеющейся, если и л/2, условия
начала скольжения основного тела вправо прп увеличении силы S не совпадают с условиями начала скольжения влево. Поэтому здесь следует различать эффективные коэффициенты при скольжении вправо (/1+) и влево (/і_) (рис. 6.2, д).
На рис. 6.1, е изображены графики зависимости относительных эффективных коэффициентов трения от отношения частоты колебаний плоскости ю к частоте свободных колебаний внутреннего тела при неподвижном основном теле k = l/c/m. Из рассмотрения графиков следует, что характер рассматриваемых эффектов резонансный: отличие коэффициентов от А - и А+ от А - существенно проявляется в диапазоне частот 0,6А: < со < <1,7к. При к/сот. е. в случае, когда внутреннее тело, по существу, жестко связано с основным, как и должно быть, А~+ = А~- и А+ — А-- Из рассмотрения рис. 6.2, е также следует, что в зависимости от зпачештя со наличие внутренней степени свободы может привести как к уменьшению, так и к увеличению эффективных коэффициентов трения. Прп этом если в определенных диапазонах изменения частоты /і+'> А~
) (или А+>А~),
то в других диапазонах могут выполняться противоположные неравенства. Это свидетельствует о том, что путем изменения частоты колебаний со при фиксированных значениях прочих параметров можно добиться изменения направления движения тела по плоскости: если Д”* = 0 п f[z} >0, то система при отсутствии силы 5 движется по плоскости вправо, а если = О и >■ 0, то влево. Этот вывод подтверждается экспериментами. Наконец, из рассмотрения графиков следует, что при м, больших некоторого значения, эффективные коэффициенты трения обращаются в нуль, что свидетельствует об «изменении характера трения» — кажущемся переходе сухого трения в вязкое.
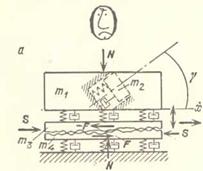
Выше речь шла о коэффициенте трения покоя /і. Относительно коэффициента трения скольжения / известно, что он всегда несколько меньше /і, однако до последнего времени не существовало объяснения этого важного факта. Сейчас имеются основания говорить о том, что «физический» коэффициент трепия скольжения не отличается от коэффициента трепия покоя, а измеряемый коэффициент трепия скольжения / является не чем иным, как эффективным коэффициентом трения при вибрации /в том смысле, в каком это понятие было определено выше. Возможность такой трактовки возникает в связи с представлением о перазрывпой связи трения скольжения и вибрации, развитым Д. М. Толстым [213, 80, 214]. Согласно этому представлению при сколь- жепии шероховатых деформируемых тел (см. модель на рис. 6.3, а) неизбежно генерируются широкополосные случайные возмущения. Прп этом возмущения, частоты которых лежат вблизи частоты свободных колебаний, обусловленных унругостью контакта, приводят, вследствие резонансного усиления, к существенным нормальным по отношению к соприкасающимся поверхностям относительным колебаниям тел (в сущности — к автоколебаниям). В процессе этих колебаний, действительно паблюдавшихся экспериментально, может даже нарушаться контакт между телами, подобно тому как это может происходить в модели, изображенной на рис. 6.2, г. В результате и происходит кажущееся снижение коэффициента тренпя /, до эффективного значения і[ь), обычно трактуемого как коэффициент трения скольжения / (рис. 6.3, б).
Любопытно, что в рассматриваемом случае позицию наблюдателя V, «не замечающего» вибрации, занимают все специалисты-механики.
Заметим, что рассматриваемый эффект может иметь место пе только вследствие отрыва (нарушения контакта) соприкасающихся поверхностей в процессе колебаний,
по также п вследствие существенно нелинейного характера сил упругости в контакте (пружинки на рис. 6.3, а; см. также работу [69]).
|
|
|
|
|
|
Если предположить в рассматриваемой модели наличие «внутренней степени свободы» (масса на пружине, изображенная на рис. 6.3, а штрихами) с конструктивной
шел полное подтверждение и успешно используется в технике (так называемые виброопоры; см., например, [12, 108]). В понятном смысле можно говорить даже о том, что вследствие вибрации коэффициент трения скольжения может принимать отрицательное значение, т. е. сила трения преобразуется в движущую силу — речь идет о вибродвигателях (вибрационных преобразователях движения), рассмотренных в п. 4.3.3.
Ситуация, подобная описанной, имеет место и при рассмотрении процессов соударения твердых тел на основе теории удара, в которой используется понятие о коэффициенте восстановления нормальной скорости R. В определенных условиях при 0 < R < 1 (частично упругий удар) возникает теоретически бесконечно ударный процесс с учащающимися соударениями тел, завершающийся за конечный (обычно небольшой) промежуток времени. Наблюдатель V, позиция которого, как и выше, имеет свои основания, будет принимать коэффициент R равным его эффективному значению R = 0. Теории указанного эффекта, называемого квазипластическим ударом, посвящена монография Р. Ф. Нагаева [159].