СИСТЕМЫ УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОВ
В регулируемых электроприводах
|
|
|
|
|
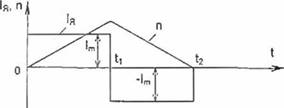
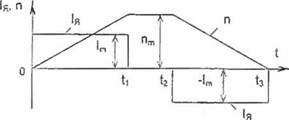
Рис. 2.1. Диаграммы тока якоря и скорости вращения двигателя |
Описанному случаю соответствует прямоугольная диаграмма тока и трапецеидальная диаграмма скорости.
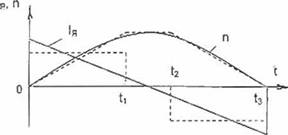
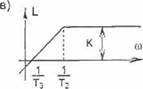
3- й случай. Учитываются ограничения (2.1), (2.2) и (2.4). Случай справедлив для электроприводов, обеспечивающих требуемую производительность при наименьших тепловых потерях з двигателе. Оптимальным переходным процессом в этом случае считают прямолинейную диаграмму тока якоря при параболическом законе изменения скорости вращения двигателя (рис. 2.1
в). Однако на практике часто отказываются от параболической диаграммы скорости. Действительно, параболу скорости на рис. 2.1 в можно легко, не уменьшая времени цикла, а следовательно. и производительности, заменить трапецией. Но последней соответствует уже прямоугольная диаграмма тока якоря. Поэтому важно знать цену отказа от линейной диаграммы тока в пользу прямоугольной. Как показывают расчеты, потери в двигателе увеличиваются не более, чем на 12%. Однако при наличии пауз в работе механизма, невозможности и нежелательности (из-за ударов в зазорах механических передач) предельно крутых фронтов нарастания тока якоря переход на параболическую диаграмму скорости практически не дает никакого дополнительного выигрыша в нагреве двигателя по сравнению с трапецеидальной диаграммой [51].
С учетом сказанного замкнутые системы управления электроприводов, работающих в пуско-тормозных режимах, строят так, чтобы обеспечить во всех случаях прямоугольную диаграмму тока якоря при трапецеидальной диаграмме скорости.
2.2 Связь частотной характеристики электропривода с кривой тока якоря при разгоне
Процессы, приведенные на рис. 2.1, характеризуют желаемые свойства системы электропривода во временной области. Выбор же структуры и величины параметров системы управления электропривода наиболее просто осуществлять, пользуясь частотными характеристиками. Поэтому требуется установить связь оптимальной кривой переходного процесса с видом желаемой частотной характеристики системы электропривода.
Идеальной прямоугольной токовой диаграмме соответствует переходная функция безынерционного звена. В этом случае логарифмическая амплитудная частотная характеристика (ЛАЧХ) системы электропривода ЭП (с входом по сигналу задания U3 и зыходом по току якоря 1я) должна быть горизонтальна во всем диапазоне частот (рис. 2.2 а).
|
|
О
|
|
|
|
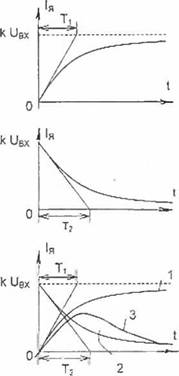
Рис. 2 2. ЛАЧХ и кривые переходных процессов в системе электропривода
обычно ограничена. В такой системе кривая переходного процесса тока якоря при разгоне двигателя отличается от прямоугольной. На рис. 2.2 изображено несколько простейших случаев, иллюстрирующих взаимную связь между кривой тока якоря при разгоне двигателя и ЛАЧХ системы электропривода.
На рис. 2.2 б ЛАЧХ системы электропривода аппроксимируется частотной характеристикой инерционного звена с передаточной функцией
W(p) = К/(1 + Ті р).
ЛАЧХ системы в области высоких частот (при > 1/Tj) понижается. Ток якоря при разгоне двигателя в такой системе электропривода изменяется по экспоненциальному закону, достигая своего установившегося значения за время, равное tM = (3...4) Ті. Чтобы увеличить крутизну переднего фронта кривой тока якоря при разгоне двигателя, нужно уменьшить постоянную времени Тt. увеличив тем самым полосу равномерного пропускания частот на кривой L.
На рис. 2.2 в ЛАЧХ и кривые процессов соответствуют реальному дифференцирующему звену с передаточной функцией
W(p) = Т3р / (1 + Т2 р) = К Т2 р / (1 + Т2 р).
ЛАЧХ этой системы электропривода в области низких частот (при со < 1/Т2) понижается. Выходная величина, увеличившись мгновенно до значения KUdx, спадает по экспоненте до нуля с постоянной времени Т2. Чтобы уменьшить темп спадания выходной величины Ія. увеличивают постоянную времени Т2, т. е. расширяют полосу равномерного пропускания частот на кривой L Для сохранения прежнего значения максимума тока якоря сохраняют неизменной величину коэффициента К. т. е. пропорционально величине Т2 увеличивают и Т3.
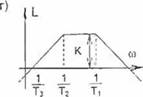
Наконец, в более общем и сложном случае (см. кривые на рис. 2.2 г) передаточная функция электропривода аппроксимируется выражением
W(p) = Т3р/(1 +Т, р)(1 +Т2р).
Приближенные показатели переходного процесса можно определить, учитывая общеизвестные зависимости между кривой переходного процесса в системе регулирования и формой ее частотной характеристики. В зоне высоких частот, определяющих характер начального участка кривой переходного процесса, реальную систему электропривода аппроксимируют инерционным звеном с постоянной времени Ті, а в зоне средних и низких частот - реальным дифференцирующим эвеном с постоянной времени Т2. Тогда на рис. 2.2 г кривую 3 переходного процесса изменения тока якоря в системе электропривода можно аппроксимировать двумя экспонентами: с постоянной времени Ті в начале процесса (кривая 1) и с постоянной времени Т2 в конце его (кривая 2). Изменением Тт и Т2 можно изменять характер переходного процесса: уменьшая Ть увеличивать крутизну переднего фронта кривой тока якоря, а увеличивая Т2, уменьшать темп спадания тока якоря после достижения его максимума.
Подведем итог сказанному. Для получения идеальной прямоугольной токовой диаграммы требуется система автоматического регулирования тока якоря с горизонтальной ЛАЧХ во всем диапазоне частот. Так как это условие в реальных системах не удается выполнить, то при синтезе системы управления добиваются максимально возможной полосы равномерного пропускания частот.
Качество настройки системы электропривода, реализующей прямоугольную токовую диаграмму, будем оценивать по следующим критериям:
а) высоте горизонтального участка ЛАЧХ системы электропривода с выходом по току якоря. В устойчивой системе регулирования максимум тока якоря при скачкообразном изменении сигнала задания не превосходит максимума амплитудной частотной характеристики, т. е.
їм * к Uex;
б) правой границе ші полосы равномерного пропускания частот системы регулирования тока якоря. Нарастание тока якоря в начале переходного процесса разгона привода происходит тем круче, чем больше ©1. Приближенно можно считать
tM ~ (3...4) / ;
в) левой границе ©2 полосы равномерного пропускания частот системы регулирования тока якоря. Чтобы обеспечить постоянство поддержания тока якоря после достижения им своего максимального значения, следует иметь наименьшего возможного значения. Приближенно время спадания тока якоря до нуля после достижения максимума
tnn ~ (3...4) / сиг.