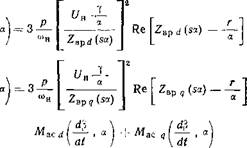СИСТЕМЫ ЧАСТОТНОГО УПРАВЛЕНИЯ СИНХРОННО-РЕАКТИВНЫМИ ДВИГАТЕЛЯМИ
Исследование переходных режимов работы синхронно-реактивного двигателя с помощью аналоговых моделирующих установок
Исходным уравнением при исследовании динамических режимов работы СРД при частотном управлении является уравнение движения привода:
Мс4Мас-Жст=/^Р, (101)
dt
где Мет — момент сопротивления на валу двигателя; J — момент инерции привода, приведенный к валу двигателя; Мс, Мас — составляющие соответственно синхронного и асинхронного электромагнитного момента двигателя; мр — механическая угловая скорость вращения ротора.
Как известно [JI. 18—20], угловое положение ротора и его угловую скорость Юр удобно измерять не относительно неподвижных осей, а относительно осей, вращающихся вместе с ротором с синхронной угловой скоростью, соответствующей частоте напряжения питания.
Для анализа динамических режимов работы СРД необходимо решить уравнение движения привода и определить зависимость изменения углового положения Р СРД от времени.
Решение уравнения (104) на электронных моделирующих установках в функции трех независимых переменных не представляется возможным, и поэтому при исследовании переходных режимов ча-
|
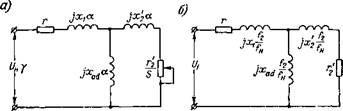
Рис 12 Схемы замещения СРД в асинхронном режиме работы для продольной оси - а — для вращающейся машины; б — для неподвижной машины при питании статора напряжением частоты h. |
стотно управляемых СРД изменением одной из переменных во времени следует задаться При дальнейшем исследовании предположим, что известным параметром является величина напряжения в зависимости от частоты, т. е. y=f{a).
При заданном характере изменения величины напряжения в зависимости от частоты уравнение движения привода примет вид:
AMP, aJ+Macf— . А— Мет =JuH~ — /— . (105)
м ' [dt ) dt р dt2
Остановимся подробнее на определении Мс (Р, а) и M&c(d$/dt, а).
Зависимость Мс(р, а) может быть найдена на основании схемы замещения СРД [см. уравнения (37) и (38)].
Для определения зависимости асинхронного момента СРД в переходном режиме работы также целесообразно воспользоваться методом схем замещения [Л. 18] по продольной и поперечной осям (рис. 12).
Для повышения точности расчета асинхронного момента параметры схем замещения асинхронного режима можно вычислить с помощью экспериментальных частотных характеристик, полученных при питании обмотки статора током переменной частоты для неподвижного ротора, соответственно снятых для его продольной и поперечной осей [J1. 21—231.
Определим входные сопротивления синхронно-реактивной машины, вращающейся с различными угловыми скоростями при переменной частоте, с помощью входных сопротивлений, найденных на основании экспериментальных измерений
Полученные входные сопротивления позволяют определить моменты СРД в асинхронном режиме работы соответственно по продольной и поперечной осям по формулам [J1. 241:
|
Я с — |
|
|
|
М |
|
ас d |
|
Мас q |
|
(107) |
|
dt d$_ dt |
)
Как указывалось выше, аналитическое решение нелинейного дифференциального уравнения, описывающего переходный режим работы СРД при переменной частоте, наиболее целесообразно выполнить на электронных моделирующих установках. При этом для
воспроизведения функции двух переменных воспользуемся методом, не требующим предварительной математической обработки кривых Мсф, а) и M&c(d$/dt, а) и применения (при моделировании) специальных функциональных преобразователей [Л. 25; 26].
Сущность этого метода заключается в следующем.
Если при изменении величины а в некоторых пределах от аь. до aft+i при расчете функций AJC(P, а) и Mac (d$/dt, а) допустимо линейное интерполирование, то эти функции в указанных пределах могут быть записаны в виде
М (Р, а. ,Л—М ($, аЛ }
Мс (м = М (Р, ak) V_1±L!
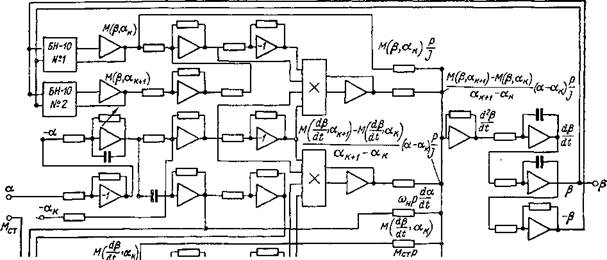
Блок-схема решения уравнения (109) с помощью электронной модели представлена на рис 13
Зависимости М(|3, а) и M(d$/dt, а) могут быть воспроизведены с помощью универсальных блоков нелинейности типа БН-10 [JI. 26].
Если линейная интерполяция невозможна во всем диапазоне изменения частот, тогда для повышения точности моделирования синхронного и асинхронного моментов двигателя целесообразно несколько усложнить схему, выделив две-три области, и воспроизвести их с помощью соответственно двух-трех блоков нелинейности. В этом случае возможно поэтапное решение задачи исследования переходного режима. При достижении величиной а определенного значения модель, работающая в программном режиме, автоматически останавливается, отключая первый нелинейный блок, и вместо него подключает следующий блок, воспроизводящий другую область моделирования моментов.
Приведенная блок-схема моделирования позволяет исследовать переходные процессы двигателя при частотном пуске и торможении, а также процессы синхронизации при изменениях нагрузки, напряжения и частоты по определенной зависимости [Л. 27].
|
|
Решение задачи синхронизации сводится к нахождению максимальных значений угла Р, при которых двигатель способен удерживаться в синхронизме с определенным качеством переходного процесса, например с апериодическим характером изменения угла в зависимости от времени.
Решение задач по исследованию переходных режимов частотноуправляемого СРД при различных законах изменения величины напряжения в функции частоты позволяет оценить эффективность управления по заданной зависимости, например по продолжительности переходного режима и характеру его изменения.