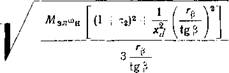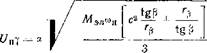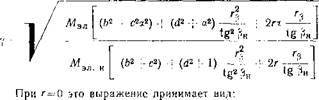СИСТЕМЫ ЧАСТОТНОГО УПРАВЛЕНИЯ СИНХРОННО-РЕАКТИВНЫМИ ДВИГАТЕЛЯМИ
Рациональные зависимости регулирования напряжения и частоты синхронно-реактивного двигателя, работающего в системе электропривода с длительным режимом
Одним из важных вопросов теории частотного управления двигателем переменного тока, работающим в системе электропривода длительного режима, является определение зависимостей изменения величины напряжения и частоты на зажимах электродвигателя для получения устойчивой работы и обеспечения наилучших с точки зрения экономичности режимов в широком диапазоне регулирования частоты (оптимальное регулирование).
Экономичность работы двигателя может быть достигнута, если при регулировании частоты напряжения питания двигателя потери в электродвигателе имеют минимальное значение, а устойчивость работы двигателя во всем диапазоне регулирования может быть обеспечена, если соответствующим образом изменять значение перегрузочной способности путем регулирования величины напряжения на зажимах обмотки статора в зависимости от частоты.
|
|
|
(52) |
|
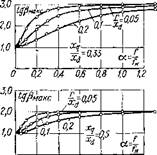
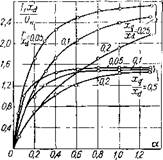
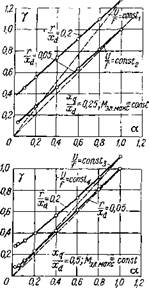
Рассмотрим рабочие характеристики СРД при регулировании величины напряжения и частоты по указанной зависимости при условии, что момент, развиваемый двигателем, остается постоянным во всем диапазоне изменения скорости вращения и равным максимальному. На рис. 4 и 5 приведены изменения величин tg0MaKc и |
Как 'известно [Л. 13], зависимость оптимального регулирования напряжения и частоты для СРД, если пренебречь влиянием активного сопротивления обмотки статора, может быть выражена следующим соотношением:
tg (Знаке, соответствующих максимальному моменту, в функции относительной частоты при различных отношениях параметров xqjxd и г[ха.
|
О 0,2 0,4 0,6 0,8 1,0 1,2 Рис. 5. Зависимости тангенса угла соответствующего максимальному электромагнитному моменту, от относительной частоты « при различных отношениях параметров х„ /х^ и rjx^ |
|
Рис. 4. Зависимости тангенса угла 6, соответствующего максимальному электромагнитному моменту синхронно-реактивного электродвигателя, от относительной частоты а при различных отношениях параметров х /х^ и /7*^' |
Из сравнения кривых рис. 4 и 5 видно, что для частотно-уп - равляемых СРД характерно уменьшение временного и пространственного углов ((Змакс, 6макс), соответствующих максимальным
электромагнитным моментам, при снижении частоты, причем это уменьшение углов более интенсивно при увеличении отношения г/хd И снижении Xq/Xd-
Уменьшение углов Рмакс И бмакс ПРИВОДИТ К Деформации формы угловой характеристики СРД [M=f(0)], повышению крутизны наклона кривой электромагнитного момента двигателя, улучшению условий самосинхронизации и устойчивости в работе.
|
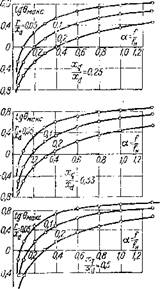
Рис. 7. Зависимости коэффициента полезного действия от относительной частоты при различных соотношениях х/хj и г/х^. |
Полученные значения углов |3Макс, бмакс позволяют определить влияние изменения частоты на коэффициент мощности cos <р, к. п. д., ток статора СРД и его электромагнитный момент.
На рис. 6, 7, 8 и 9 показаны зависимости cos ф, к. п. д., тока 11 и электромагнитного момента в функции относительной частоты при различных отношениях
|
О 0,2 0.4 0,6 0,8 1,0 1,2 |
параметров Xq/Xd, rfXd и углах Рмакс, соответствующих максимальному значению электромагнитного момента.
|
Рис. 8. Кривые изменения тока статора синхронно-реактивного двигателя в зависимости от относительной частоты при различных отношениях параметров xa^xdM r! xd- |
|
Рис. 6. Зависимости коэффициента мощности синхронно-реактивного двигателя от относительной частоты при моменте сопротивления, равном максимальному моменту двигателя, и различных соотношениях параметров X /X^ И А/Хд. |
|
1,6 1,2 0,8 0,4 |
|
0,4 |
|
0,4 |
1,2
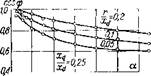
Рис. 9. Кривые значений максимального электромагнитного момента синхронно-реактивного двигателя при изменении величины напряжения и относительной частоты по зависимости L///=const при различных отношениях xqlxfr и rlxd.
Как видно из кривых рис. б, 7, 8 и 3, активное сопротивление обмотки статора существенно влияет на характеристики двигателя. С понижением частоты монотонно уменьшаются электромагнитный к. п. д., максимальный момент и ток двигателя, повышается коэффициент мощности.
Анализ рабочих характеристик СРД показывает, что регулирование напряжения по зависимости (52) в широком диапазоне изменения частоты при постоянном моменте сопротивления на валу СРД не обеспечивает определенного, постоянного значения перегрузочной способности вследствие усиливающегося при снижении частоты влияния активного сопротивления обмотки статора. Это обстоятельство приводит, как известно, к необходимости выбора мощности двигателя из условий обеспечения устойчивой работы на минимальной частоте и, следовательно, к большим недогрузкам, ухудшению энергетических показателей при работе СРД в области повышенных частот и снижению диапазона регулирования двигателя.
Для определения зависимости величины напряжения и частоты его изменения, обеспечивающей при заданном моменте сопротивления на валу любое заданное значение перегрузочной способности трехфазного СРД с учетом влияния активного сопротивления обмотки статора, запишем вначале отношение уравнений максимального электромагнитного момента двигателя к моменту двигателя и решим полученное уравнение относительно параметра tg р.
На основании (37) и (41)
|
|
|
(&2 _j_ с2а2) -.L (с(2 _|_ а2) |
|
Мг |
|
(53) |
|
М, |
|
2 [l' (d2 j «2) _|_ с2а2) _j_ га] tg? |
|
откуда (tg Р)2 + |
|
|
|
эл. макс 8 |
|
d 2 |
|
2 М |
|
2 ГЯГя |
|
М: |
|
Ь2 f - С2аа |
|
2Мэл. макс-2т^ Мэл (Ь2 г с‘2а2) |
|
tg Р ■ ь |
|
(54) |
|
0. |
|
Ь2 С2Я2 J Р |
|
|
Далее по полученным из уравнений (54) значениям tg (3 при различных заданных значениях а и момента сопротивления, равного моменту двигателя Мэл, определим значение тока из уравнения (39):
(55)
Подставив полученное значение тока в уравнение (35) и решив его относительно параметра у, найдем зависимость регулирования
величины напряжения в функции частоты а, обеспечивающую любое заданное значение перегрузочной способности СРД, в общем виде:
|
|
(56)
где tg |3 определяется из выражения (54).
Полагая активное сопротивление статора г=0 в выражении
(56) ,- получаем зависимость регулирования величины напряжения и относительной частоты его изменения при любых заданных значениях момента сопротивления и перегрузочной способности двигателя:
|
|
(57)
В частном случае, при постоянном моменте спротивления на валу двигателя, постоянство перегрузочной способности двигателя достигается в том случае, если максимальный момент при любой относительной частоте а будет равен максимальному моменту при а=1 и у = 1 •'
3 и
М =______________ 5___________ . Г58^
эл. макс г,/ і v >
2сон [у (* + 1) (6* + С*) + rj
Разделив (41) на (58), получим зависимость параметра у, характеризующего изменение величины напряжения, от частоты, обеспечивающую постоянную перегрузочную способность при Мэл. макс = = const:
V(d2 + «2) (6* + С%2)
+ V{<P+ 1) (Ь2 + с*)
При г=0 это выражение может быть записано в общеизвестном виде [J1. 131:
У = а, т. е. —^ = — = const. (60)
Ub /н
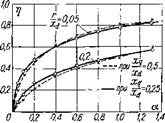
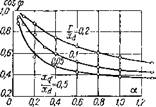
На рис. 10 представлены зависимости величины напряжения от частоты, обеспечивающие постоянство перегрузочной способности СРД при различных соотношениях параметров xq/xd и г/ха и моменте сопротивления М~ const.
Из приведенных кривых видно, что зависимость регулирования величины напряжения и частоты по уравнению (59) значительно отличается от зависимости регулирования напряжения и частоты при пренебрежении активным сопротивлением обмотки статора [см. выражение (60), на рисунке—пунктирные прямые), особенно в области низких частот (а=00,1) при небольших значениях xq/xd и повышенных значениях г/ха-Ё этом случае расчеты по формуле (60), т. е. без учета влияния активного сопротивления, приводят к недопустимым погрешностям, превосходящим 100%.
Для того чтобы выявить особенности работы СРД в режиме постоянства перегрузочной способности (при постоянно]^ значении
|
|
|
М |
|
Рис. 10. Зависимости напряжения от частоты в относительных единицах, обеспечивающие постоянство перегрузочной способности ■ синхронно-реактивного двигателя при постоянном моменте сопротивления и различных соотношениях X /X^ и r/xd. |
момента сопротивления на валу), целесообразно сравнить этот режим с достаточно хорошо изученным аналогичным режимом частотно-управ - ляемого асинхронного двигателя [Л. 3].
Как известно, при работе асинхронного двигателя в режиме, характеризующемся постоянством перегрузочной способности (при постоянном моменте сопротивления на валу) по всему диапазону регулирования, при снижении частоты магнитный поток двигателя существенно увеличивается и в пределе, когда частота приближается к нулю, в несколько раз превосходит номинальное значение.
Для приблизительной оценки изменения магнитного потока Ф асинхронного двигателя при частотном управлении можно воспользоваться уравнением для максимального электромагнитного момента
2aKL
|
эл. макс АД |
kx Ф2
где sK — скольжение, соответствующее максимальному электромагнитному моменту при номинальной частоте (критическое); k—постоянный коэффициент; г2' и х2 — параметры ротора асинхронного двигателя.
Принимая во внимание, что для асинхронных электродвигателей небольшой мощности (до 10 кет) х2~(2-г- 4)г2', и пренебрегая величиной (*2'sKa) 2 в 30не низких частот, уравнение (61) можно записать в следующем виде: Мэл. макс~&Ф2а, откуда
|
kM, |
|
(62) |
|
Ф |
|
V |
Из уравнения (62) видно, что при изменении частоты в диапазоне 1—0,01 и при неизменном моменте двигателя его магнитный поток изменяется приблизительно в 10 раз.
Значительное увеличение магнитного потока сопровождается насыщением стали, чрезмерным возрастанием намагничивающего тока, потерь в меди и приводит к тому, что реализация режима ра-
боты асинхронного двигателя, обеспечивающего постоянство перегрузочной способности по всему диапазону регулирования, затруднительна.
Нетрудно показать, что поведение СРД в режиме постоянства перегрузочной способности отличается от аналогичного режима асинхронного двигателя.
На основании уравнений (41) и (44) уравнение для максимального электромагнитного момента СРД при переменной частоте можно представить в виде
Л/f Гр ^ ^макс
тэл. макс СРД 2 о о—;---------- > (63)
4 + 4 ^макс
где k2 — постоянный коэффициент.
Если учесть, что обычно СРД конструктивно выполняется со значениями отношения индуктивных параметров в пределах xq[xd = = 0,5-ь 0,25, а кратность изменения tg (Змакс, соответствующего максимальному электромагнитному моменту в диапазоне регулирования частоты 1 : 100, составляет 3—4 (см. рис. 5), из уравнения (63) следует, что магнитный поток двигателя при неизменном максимальном моменте изменяется приблизительно в 1,3—1,4 раза. Такое изменение магнитного потока не вызывает чрезмерного увеличения намагничивающего тока, и, следовательно, получение больших диапазонов регулирования для СРД с постоянной перегрузочной способностью практически не встречает серьезных затруднений.
Таким образом, магнитный поток и ток СРД, работающего в режиме постоянства перегрузочной способности, возрастают незначительно по отношению к их номинальным значениям и не приводят к чрезмерному увеличению потерь при снижении частоты по сравнению с аналогичным режимом работы асинхронной машины.
|
|
Учитывая, что форсировка магнитного потока все же сопровождается увеличением тока двигателя, потерь и его нагрева, целесообразно рассмотреть режим управления величиной напряжения и относительной частотой, при котором магнитный поток изменяется пропорционально корню квадратному из момента нагрузки:
(64)
В этом случае при постоянном моменте нагрузки на валу магнитный поток двигателя остается неизменным при любом значении частоты напряжения питания и не приводит к увеличению намагничивающего тока и потерь.
Приравняв выражения для электромагнитного момента (66) и (37) и решив это равенство относительно параметра у, зависимость величины напряжения от частоты его изменения, обеспечивающую режим работы с постоянным, заданным значением магнитного потока, можно представить в следующем виде:
При г—О уравнение (67) преобразуется в уравнение — = const.
Нетрудно показать, что при регулировании величины напряжения и его частоты по зависимости, согласно которой магнитный поток двигателя изменяется по уравнению (64), момент, развиваемый двигателем, при заданной величине потока не зависит от частоты, а величина угла р сохраняется постоянной и равной номинальной.
Связывая величину момента, развиваемого двигателем, с его магнитным потоком, получаем
*8 tg
Подставляя в это выражение значение магнитного потока из уравнения (64), имеем
|
(69) |
|
М. |
|
Ык |
|
rfi tg I |
Это соотношение справедливо при условии, если tg|3=tgpH - Перегрузочная способность СРД при регулировании магнитного потока по соотношению (64) равна
|
М' |
^ __ ^эл. макс ___ tg
2xBrs tg
и остается неизменной при изменении момента нагрузки и частоты.
Анализ рабочих характеристик СРД при регулировании его магнитного потока по уравнению (64) показывает, что они полностью соответствуют характеристикам режима регулирования СРД но зависимости (52), если сопротивление обмотки статора двигателя равно нулю. В результате двигатель на всех частотах находится в условиях, наиболее близких к его работе при номинальной частоте.
Как известно, система регулируемого электропривода с применением СРД позволяет обеспечить синхронное вращение нескольких электродвигателей с неизменным углом р.
Для определения зависимости изменения величины напряжения и частоты, обеспечивающей постоянство угла |3, воспользуемся уравнениями электромагнитного момента:
|
ЗІ і |
Разделив выражение (72) на (71), получим уравнение для определения указанной зависимости:
|
|
|
|
(74)
Режим работы СРД с постоянным углом (3 отличается от режима работы с постоянным магнитным потоком тем, что с увеличением момента нагрузки магнитный поток двигателя также увеличивается.
Недостатком режима постоянства угла (3 является уменьшение по мере снижения частоты величины статической перегружаемости двигателя вследствие деформации угловых характеристик и изменения углов, соответствующих максимальному моменту двигателя.
Из уравнений (59), (67) и (73) видно, что, если пренебречь активным сопротивлением обмотки статора, можно получить зависимость регулирования СРД, аналогичную по виду оптимальной зависимости регулирования для асинхронного двигателя. Эта зависимость напряжения и частоты обеспечивает наибольшую экономичность, постоянную перегрузочную способность и постоянное значение угла [3 при изменении частоты и нагрузки.
Приведенные выше зависимости регулирования напряжения и частоты, согласно которым перегрузочная способность или угол (3 могут принимать любые заданные значения (например, постоянные значения по всему диапазону регулирования) с учетом влияния активного сопротивления обмотки статора, показывают, что
оптимальный режим работы СРД не может быть обеспечен но всем указанным признакам (X=const, Ф = const, (3=eonst) при изменении частоты из-за влияния падения напряжения на активном сопротивлении обмотки статора, деформации угловых характеристик [М = =/'(Р)] и изменения значения углов [3, соответствующих максимальному моменту двигателя.
Оптимальный режим работы СРД может быть получен, если при регулировании напряжения и частоты магнитный поток двигателя изменяется по зависимости (64).
При разработке схем управления электроприводами с частотным регулированием СРД возникает задача создания взаимосвязанного управления тремя параметрами: величиной напряжения, частотой его изменения и моментом.
Реализация этих зависимостей изменения напряжения, частоты и момента двигателя в системах регулируемого электропривода с СРД осуществляется соответствующим построением схем управления. Наиболее просто это достигается при условии, что система управления позволяет изменять величину напряжения и его частоту на зажимах СРД независимо друг от друга.