ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ С ЧАСТОТНОЗАВИСИМЫМИ ЦЕПЯМИ
Принципы преобразования информации с помощью частотно-зависимых цепей
Один из простейших принципов преобразования информаций с помощью ЧЗЦ основан на использовании частотных характеристик ЧЗЦ, если частота входного сигнала преобразуется в напряжение по законам, соответствующим различным функциональным зависимостям. На этом принципе строятся простейшие ИП непосредственного преобразования, выполняемые (рис. 1.1) путем сочетания ЧЗЦ, реализованной в виде частотно-зависимого четырехполюсника (ЧЗЧ), и выходного устройства (ВУ), преобразующего определенный параметр выходного сигнала ЧЗЧ в напряжение постоянного тока UB ых - При синусоидальной форме входного сигнала ИП вид используемой частотной характеристики ЧЗЧ определяется типом ВУ [6].
Если ВУ представляет собой амплитудный выпрямитель или выпрямитель— преобразователь среднего значения напряжения, то функциональная зависимость между частотой входного сигнала и выходным напряжением постоянного тока соответствует амплитудно-частотной характеристике ЧЗЧ. Для получения зависимости, соответствующей вещественной или мнимой части амплитудно-фазовой характеристики, В$ выполняют в виде фазочувствительного выпрямителя, в качестве опорного напряжения которого используется входной сигнал, подаваемый непосредственно или со сдвигом по фазе на 90°. Для получения зависимости, соответствующей фазочастотной характеристике, ВУ выполняют в виде аналогового измерителя фазового сдвига между двумя синусоидальными напряжениями [7].
Во всех этих случаях ИП является, по существу, функциональным преобразователем частоты в напряжение (ФПЧН), реализующим зависимость, определяемую в общем случае равенством
UBhix—0((o)=kUfF((o)y (1-1)
где Uf — амплитуда входного синусоидального сигнала с частотой /; <о=2л/ — круговая частота; F(со)—используемая частотная характеристика ЧЗЧ; k — постоянный коэффициент, зависящий от параметров ВУ. При использовании фазочастотной характеристики величина Uf в (1.1) заменяется амплитудой опорного напряжения U0.
Если входной сигнал имеет форму однополярных прямоугольных импульсов (рис. 1.2), имеющих длительность т и следующих с частотой /, то ЧЗЧ может быть выполнен в виде последовательно соединенных фильтра верхних частот и однополупериодного выпрямителя [8]. Фильтр верхних частот не пропускает постоянную составляющую последовательности импульсов, поступающей на него, в результате чего на его выходе образуется последовательность двухполярных импульсов, в которой, как известно, амплитуды положительных и отрицательных импульсов соответственно равны:
£/т+ = £/т(Г-Т)/Г=£/т(1-Є); Um-=Umt/T=UmB, (1.2)
|
Рис. 1.1. Обобщенная структурная схема ИП непосредственного преобразования |
где Um амплитуда входных импульсов; T=l/f — период следования импульсов; 0=т/7 — относительная длительность импульсов.
к---7'-!
Рис. 1.2. Импульсный входной сигнал ИП
На выходе однополупериодного выпрямителя образуется последовательность однополярных импульсов с амплитудой, зависящей от значения 0 согласно одному из выражений (1.2). В результате подобный ЧЗЧ выполняет функцию преобразователя относительной длительности прямоугольных импульсов в их амплитуду (ПДА).
Величина 0 может соответствовать в равной мере как переменной частоте / следования импульсов постоянной длительности т=т0 (пр» этом 0=To/7'=Tof), так и переменной длительности т импульсов, следующих с постоянной частотой. Поэтому рассматриваемый импульсный сигнал в общем случае является частотно-временным и характеризуется величиной 0 как обобщенным информативным параметром. Следовательно, зависимость амплитуды выходных импульсов ПДА от величины 0 можно рассматривать как амплитудно-частотную характеристику ПДА. В зависимости от полярности напряжения на входе однополупериодного выпрямителя эта характеристика имеет вид одной из линейных функций Z7(0) = 1—0 или F(0)=0, причем данное преобразование выполняется без изменения фазы импульсов. На основе каскадного соединения лодобных простейших преобразователей можно получать ПДА с характеристиками F(0) в виде степенных полиномов (см. § 2.2), с помощью которых можно аппроксимировать различные трансцёндент - ные функциональные зависимости.
Измерительный преобразователь простейшей структуры (см. рис. 1.1), в котором в качевтве ЧЗЦ используется ПДА, а в качествеВУ—амплитудный выпрямитель, реализует функцию преобразования
£/вых=&£/«/7(0), (1-3)
аналогичную функции (1.1) для синусоидального входного сигнала при том же типе ВУ. Однако если в качестве ВУ применен преобразователь среднего значения напряжения, то в функции преобразования амплитудно-частотная характеристика F(Q) заменяется одной из зависимостей 0/7(0) или (1—в)/7(0) (см. § 2.4).
|
Х1
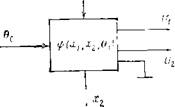
Рис. 1.3. Схема ЧЗЦ уравновешивания |
Использование метода следящего преобразования позволяет получить широкий набор возможных вариантов входных и выходных переменных в прямых и обратных ИП соответственно. Следящее преобразование реализуется на основе ЧЗЦ уравновешивания, питаемой напряжением выходного (входного для обратных ИП) сигнала ИП и содержащей элементы с параметрами, зависящими от входных переменных Х и х2 (от выходной переменной х2 для обратных ИП), или с непосредственно преобразуемыми параметрами, а также управляемые элементы с частотно-зависимыми параметрами. В качестве управляющих параметров используются параметры f или 0 входного сигнала элемента, т. е. параметры напряжения питания ЧЗЦ. Следовательно, отдельные управляющие входы имеются только у элементов, параметры которых зависят от переменных Х и х2. Частотно-зависимую цепь уравновешивания можно изобразить как многополюсник (рис. 1.3) с входами для подачи переменных 0О, Х и х2 и двумя выходами, на которых наблюдаются напряжения Ux и U2. Для общности через 0о здесь обозначена переменная, которая может соответствовать как частоте f синусоидального сигнала, так и параметру 0 импульсного сиг - нала. В качестве переменных хх и х2 могут использоваться, например, механическое перемещение, цифровой код и относительная длительность прямоугольных импульсов, следующих с частотой, значительно большей частоты выходного (входного) сигнала ИП.
Цепи уравновешивания характеризуются возможностью установления состояния равновесия или квазиравновесия, при котором соответственно
U = U2 или U{ = U2. (1.4)
В общем случае выходные напряжения U{ и U2 зависят от трех входных переменных:
Выполнение однего из равенств (1.4) эквивалентно получению уравнения
которое называется условием равновесия (квазиравновесия) ЧЗЦ уравновешивания. Общий вид условия равновесия (1.6), очевидно, сохраняется и в случаях, когда зависимости (1.5) «неполные», например когда напряжение U зависит только от переменных Х и х2, а напряжение U2 — только от переменной 0о. Заметим, что состояние квазиравновесия может характеризоваться не только равенством |£Л| = |^2І, но и любым другим условием, налагаемым на параметры сигналов U, и U2.
Работа следящих ИП состоит в том, что при изменениях входных переменных, вызывающих нарушение условия равновесия ЧЗЦ, на ее выходе возникает сигнал разбаланса —U2 или |£Л| — U2, который после усиления и соответствующего преобразования приводит к изменениям выходной переменной, обеспечивающим восстановление условия равновесия. При этом, в принципе, безразлично, какие из входных переменных хи х2 или 0о являются независимыми, т. е. входными для ИП в целом, а какая из них используется для поддержания условия равновесия и является выходным параметром ИП. Отсюда следует возможность обратимости следящих ИП с ЧЗЦ, т. е. возможность реализации как прямых, так и соответствующих им обратных ИП на основе одних и тех же ЧЗЦ уравновешивания.
Конкретный вид условия (1.6) определяет вид реализуемого преобразования хи *2-^00 или хи 0о-**2 в прямых и обратных ИП соответственно. В большинстве случаев ИП работают с одной входной (выходной) переменной, и указанное преобразование можно записать в виде *-*-0о или 0о->*.
Работа ИП развертывающего преобразования основана на использовании периодически изменяющихся напряжений — так называемых езвертывающих функций U=R{i), где t — время. В прямых ИП раз - i-ртывающего преобразования фиксация соответствующего моменті времени осуществляется в момент равенства текущего значения раз - ертывающей функции значению входного сигнала, а в обратных ИП азвертывающего преобразования — в определенный момент времени* определяемый значением преобразуемой переменной, фиксируется значение развертывающей функции. Во всех типах ИП развертывающего преобразования формирование развертывающих функдий фактически выполняется с помощью ЧЗЦ, которые или входят в состав генерато* ров импульсных напряжений требуемой формы, или преобразуют фор* му подаваемых на них прямоугольных импульсов. В отличие от ИП непосредственного преобразования и ИП следящего преобразования в ИП развертывающего преобразования непосредственно используютвя не частотные, а переходные характеристики ЧЗЦ. Эта особенность су* щественно влияет на выбор ЧЗЦ. Например, для получения линейных развертывающих функций широко используются интеграторы, которые можно рассматривать как ЧЗЦ, реализованные в виде активных ЧЗЧ с амплитудно-частотной характеристикой, соответствующей закону обратной пропорциональности.