Ламбертовское распределение излучения
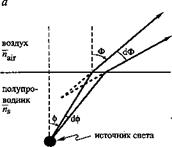
Различия между показателями преломления излучающего материала и окружающей среды ведет к анизотропии пространственного распределения излучения. Для планарных диодов на основе материалов с высокими значениями показателей преломления характерно ламбертовское распределение излучения. На рис. 5.4 показан точечный источник излучения, расположенный немного ниже границы раздела полупроводник-воздух. Луч, выходящий из источника света под углом <р с нормалью к поверхности раздела, преломляется под углом Ф также по отношению к нормали. Углы /р и Ф связаны законом Снеллиуса, поэтому для малых углов <р (sinip « <р) можно записать соотношение
ns • sin ip ns • <p — nair • sin Ф. (5.26)
|
|
Луч света, испускаемый в полупроводнике в пределах конуса с углом d<j>, отразившись от поверхности раздела, попадет в воздухе в сектор, определяемый углом d$ (все по отношению к нормали) (см. рис. 5.4, а). Дифференцируя выражение (5.26) по углу Ф и решая полученное
|
|
|
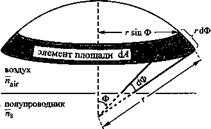
Рис. 5.4. Геометрическая модель, используемая для вывода уравнения для ламбертовского распределения: а — свет, излучаемый в пределах угла (1ф внутри полупроводника, в воздухе излучается в пределах угла <й>; б — иллюстрация элемента поверхности сегмента сферы |
|
Паіг COS Ф |
|
уравнение относительно с1Ф, получаем |
(5.27)
Из закона сохранения энергии следует, что мощность оптического излучения в пределах угла dtp в полупроводнике должна равняться оптической мощности излучения в воздухе в пределах угла сіФ, т. е.:
|
(5.28) |
Is ‘ dAs — /ajr' dAajy,
где Is и lair — интенсивности излучения в полупроводнике и в воздухе, измеренные в единицах Вт/м2. Исходя из цилиндрической симметрии диаграммы направленности, выбираем элемент поверхности, показанный на рис. 5.4, б. Площадь этого элемента определяется выражением
|
(5.29) |
|
|
dAair = 27Г • г • sin Ф • r с£Ф. Используя уравнения (5.27) и (5.28), получаем
(5.30)
Аналогично этому, площадь элемента поверхности полупроводника определяется выражением
dAs = 2-к ■ г ■ smy? • г dip « 27г г2 ■ <р • dtp. (5.31)
Интенсивность излучения внутри полупроводника на расстоянии г от поверхности находится делением полной мощности источника света на площадь поверхности сферы радиуса г:

|
|
|
source |
|
4жг2 |
(5.32)
Интенсивность излучения в воздухе находят совместным решением уравнений (5.28), (5.30), (5.31) и (5.32). Результирующее выражение и является уравнением для ламбертовского пространственного распределения:
/а1г = . cos ф. (5.33)
Аж г ns
Из этого выражения видна зависимость интенсивности излучения по функции косинуса от угла Ф. Это означает, что интенсивность света максимальна при излучении, перпендикулярном поверхности полупроводника при Ф = 0°. При угле Ф = 60° интенсивность снижается до значения, равного половине максимума. На рис. 5.5 схематично показано ламбертовское пространственное распределение излучения (диаграмма направленности, или, как принято в светотехнике, кривая силы света) планарного светодиода.
|
а |
б |
в |
|
полупро |
j излучающая |
|
|
водник. г |
*ф jу/ область |
|
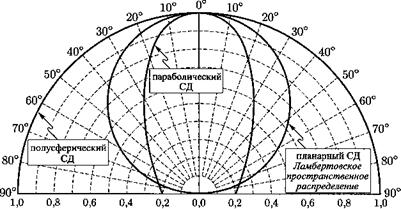
Рис. 5.5. Светодиоды с планарной (а), полусферической (б) и параболической (в) поверхностями; пространственное распределение излучения разных типов светодиодов (г). При Ф = 60° интенсивность ламбертовского распределения излучения уменьшается до значения, равного половине максимума, достигаемого при Ф = 0°. Приведенные пространственные распределения нормированы так, что при Ф = 0° интенсивность равна единице |
|
|
На рис. 5.5 приведены примеры светодиодов с поверхностями другой геометрической формы и характерные для них пространственные распределения излучения. Для полусферического светодиода характерно изотропное пространственное распределение с излучающей областью в центре сферы. При параболической форме поверхности получается распределение с ярко выраженной направленностью. Однако светодиоды с параболической и полусферической поверхностями гораздо сложнее изготовить, чем планарные светодиоды.
Полную мощность излучения, выведенного в воздух, можно найти, интегрируя интенсивность излучения вдоль всей поверхности полусферы:
90° '
Pair = /аіг • 27Г • Г • sin Ф • Г (1Ф. Ф=0°
Подставляя уравнение (5.33) в (5.34) и считая, что cos Ф • sin Ф = = (1/2)вш(2Ф),
|
|
(5.35)
Таким образом, получился результат, идентичный уравнению (5.24). Это не удивительно, поскольку мощность излучения полупроводника (Реscape) должна быть равна МОЩНОСТИ излучения В воздухе (Pair)- Правда, следует отметить, что во всех приведенных расчетах не учитывались формулы Френеля при отражении на границе раздела полупроводник-воздух. При нормальном падении лучей на поверхность потери мощности излучения за счет отражения по формулам Френеля можно оценить по выражению
|
В строгих расчетах пренебрегать потерями на френелевское отражение нельзя. Упражнение. Определение эффективности связи светодиод-оптическое волокно Рассматривается планарный светодиод GaAs с точечной излучающей областью, расположенной в непосредственной близости от поверхности. Входная угловая апертура оптического волоконного световода равна 12°. Требуется определить долю излучения из активной области светодиода, попадающую в оптический волоконный световод. Считается, что показатель преломления GaAs ns = 3,4. Потерями на отражение Френеля на границах раздела полупроводник-воздух и воздух-оптическое волокно можно пренебречь. Решение Угловая апертура полупроводникового светодиода, найденная по закону Снеллиуса, равна 3,5°. Поэтому доля излучения из активной области светодиода, попадающая в оптическое волокно, составляет всего 0,093 %. |