ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
ЭНЕРГЕТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ АСИНХРОННЫХ ЭЛЕКТРОПРИВОДОВ
4.2.1. Кинематически связанные электроприводы
В гл. 3 было показано, что постоянные потери асинхронного электропривода не зависят от его нагрузки и остаются практически неизменными при неизменной скорости. Вместе с тем переменные потери, к которым отнесены потери в меди статора и ротора, зависят от нагрузки. Имеется большое число механизмов, в которых нагрузка электропривода зависит от характеристик механизма, на которые можно повлиять в процессе проектирования, наладки и даже эксплуатации.
В качестве примера рассмотрим многодвигательные электроприводы таких механизмов, как рольганги, механизмы перемещения крана, поворота платформы экскаватора, различных транспортных машин и т. д. Достаточно часто электроприводы механизмов выполняют двух - или многодвигательными для уменьшения их
момента инерции, что позволяет улучшить динамику процессов. Во всех этих механизмах скорость двигателей, как правило, одинакова, а распределение статической нагрузки, если не приняты специальные меры, оказывается неравномерным.
|
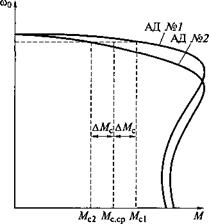
Рис. 4.1. Распределение момента нагрузки между двумя параллельно работающими двигателями |
Причиной неравномерной нагрузки двигателей обычно является незначительное отличие механических статических характеристик двигателей. Нарис. 4.1. представлены механические характеристики двух одинаковых асинхронных двигателей при питании их от сети. При одинаковой частоте вращения моменты двигателей соответственно
для АД № 1 и АД № 2 определяются выражениями:
Mcl — -^с. ср ATWg, A/q2 -^с. ср
где ЛГс. ср — среднее значение статического момента, Мс ср = (Мс] + + Мс2)/2; АМс — отклонение статического момента от среднего.
Очевидно, что аналогичная картина будет наблюдаться и в регулируемых электроприводах. Причиной этого является как разброс параметров отдельных двигателей, так и различие в настройках систем управления. Оценим влияние неравномерности деления нагрузок на потери энергии в двигателе.
Переменные потери энергии в двигателе (потери в меди статора и ротора) можно выразить через механические переменные:
APM = Mu0S(l +а), (4.1)
где а = Ri/R'2.
Так как работа двигателя в двигательном режиме происходит на линейном участке механической характеристики, то скольжение двигателя можно достаточно точно выразить через его момент:
|
s = |
М
(4.2)
No ’
где (3 — жесткость линейного участка механической характеристики, Р = ^номА^о*$ном*
Тогда
(4.3)
|
Потери в меди в номинальном режиме работы двигателя (при М - Мном) составят |
|
1 + а 1” |
|
М2 1Y1 ном • |
|
АЛ, |
|
(4.4) |
|
Тогда при работе двигателя с моментом, отличным от номинального, потери в меди А Рм = &Рм. ном(М/Мном)2. Для приведенного выше примера потери в меди первого двигателя составят |
|
Мс ср + А Мс у |
|
(4.5) |
|
А^м(і) — А РМЛЮи |
|
для второго |
|
Мс. ср - АМс |
|
(4.6) |
|
^^м(2) — АРм. ном |
|
а суммарные потери в двух двигателях — АРМ2 = 2аРм |
|
М2С р + А М2 |
|
(4.7) |
|
М2 Ш нг |
|
Очевидно, что если двигатели загружены одинаково, то суммарные потери в двух двигателях |
|
•^с. ср Мн0м |
|
АРиЪ = 2АЛ |
|
т. е. меньше на величину дополнительных потерь AM2 |
|
= 2А Ры |
|
(4.8) |
|
АР, |
|
м£доп |
|
м2 1УЛ ном |
|
В качестве примера выполним расчет потерь в меди в двух двигателях типа МТМ412-6, работающих на общую нагрузку. Двигатели имеют следующие номинальные данные: Рном - 22 кВт; соном = 100,51 с"1; SH0U = 0,04; Rx = 0,218 Ом; R'2= 0,1922 Ом. Потери в меди в номинальном режиме работы в соответствии с формулой (4.4) составят АРМ. Н0М = 1,95 кВт = 0,09 Рном. Если Мс ср = 0,5Мном, то при АМс = 0,2 Мноы потери в двигателе с большей нагрузкой в соответствии с формулой (4.5) составят АРм(1) = |
= 0,72ДРМ ном = 0,49ДРНом=0,956 кВт, а в двигателе с меньшей нагрузкой В СООТВеТСТВИИ С формулой (4.6) ДРМ(2) = 0,32ДРМ ном = 0,09ДРцом = = 0,176 кВт.
Суммарные потери в двух двигателях ДPuZ = 0,58 ДРМ Н0М =1,131 кВт.
При равномерном делении нагрузки АРм1_ = 0,5ДРМ НОМ = 0,975 кВт.
Дополнительные потери в меди при неравномерном делении нагрузки ДРм2;доп = 0,08ДРМ НОМ = 0,156 кВт.
Если АМС = 0,5Мнои, то дополнительные потери в меди обоих двигателей возрастут до величины ДРм5;доп = 0,5ДРМ ном = 0,975 кВт.
На первый взгляд экономия энергии за счет выравнивания нагрузок этих двигателей незначительна, но следует учесть два обстоятельства. Во-первых, затраты на выравнивание нагрузок двигателей, как правило, невелики. Так, в случае использования двигателей с фазным ротором это может быть сделано за счет небольшого изменения дополнительных сопротивлений в цепи ротора. В системах ТПН—АД и ППЧ—АД это потребует более тщательной настройки регуляторов электроприводов и более точного формирования сигналов заданий на электроприводы. Во - вторых, при массовом использовании таких электроприводов суммарная экономия энергии может быть ощутимой.
Аналогичные рекомендации могут быть даны и для главных электроприводов многоклетьевых прокатных станов, намоточноразмоточных устройств, в которых технологический процесс происходит с определенным натяжением обрабатываемого материала. Очевидно, что работа таких электроприводов с минимально необходимым натяжением сопровождается уменьшением потерь в двигателях.
4.2.2. Режимы энергосбережения в электроприводах с полупроводниковыми преобразователями
Некоторые современные полупроводниковые преобразователи (ТПН и ППЧ) в виде дополнительной функции содержат так называемый режим энергосбережения. Рассмотрим возможности этого режима на примере преобразователя частоты со скалярным управлением.
В гл. 3 было показано, что средством дополнительного энергосбережения при частотном управлении асинхронным двигателем является разработка такого алгоритма управления, который оптимизировал бы магнитный поток. Оптимизация магнитного потока позволяет несколько снизить потребляемую мощность путем снижения уровня напряжения при работе в установившемся режиме. В переходных режимах следует использовать регулирование с номинальным потоком, так как работа с оптимальным по условиям энергосбережения магнитным потоком связана с существенным уменьшением перегрузочной способности двигателя, что не позволяет достичь необходимого динамического момента.
Для того чтобы оценить эффективность оптимизации магнитного потока, можно воспользоваться схемой замещения асинхронного двигателя (см. рис. 1.2) для анализа установившихся режимов работы АД. Задача заключается в том, чтобы при заданном моменте нагрузки и заданной скорости ротора определить такие значения частоты и амплитуды напряжения, при которых обеспечивается минимум потерь в двигателе. Так как при фиксированных моменте и скорости механическая мощность не изменяется, то минимум потерь соответствует минимуму потребляемой мощности и максимуму КПД двигателя. Получение аналитического выражения для амплитуды и частоты напряжения затруднено из - за сложности системы уравнений асинхронного электропривода, которая включает векторные величины и комплексные сопротивления, зависящие от скольжения и скорости вращения магнитного поля. Вместо этого приведем результаты численного решения этих уравнений без учета возможного изменения параметров схемы замещения. Алгоритм решения выглядит следующим образом:
• задается момент нагрузки Мс и угловая скорость со;
• задается действующее значение напряжения Ub приложенного к двигателю;
• численно находится такая скорость со0, которая при расчете электромагнитного момента М дает результат М - Мс;
• рассчитываются суммарные потери энергии в двигателе;
• в процессе расчета определяется точка с минимумом потерь энергии и все параметры, соответствующие этой точке.
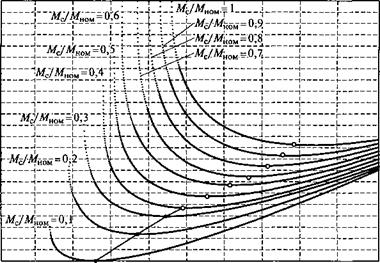
Проанализируем некоторые результаты моделирования по указанному алгоритму для двигателя типа 4A160S2, имеющего Рнш = 15 кВт. На рис. 4.2 показаны зависимости потерь от амплитуды напряжения и моментов нагрузки при со = соном (а) и со = 0,5соном (б). Как видно на рис. 4.2, а, возможность снижения потерь имеется лишь при моментах сопротивления Мс < 0,6Мном. Очевидно, что при снижении скорости диапазон моментов нагрузки, в котором целесообразно снижать напряжение, уменьшается (см. рис. 4.2, б). В этом случае не рассматривается возможность увеличения напряжения, так как оно приведет к насыщению магнитной цепи.
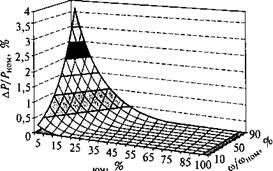
Возможности экономии потребляемой мощности при различных скоростях и моментах двигателя типа 4A160S2 сведены в табл. 4.1, а на рис. 4.3 показана диаграмма, наглядно иллюстрирующая экономию потребляемой мощности в зависимости от скорости и момента статической нагрузки двигателя типа 4A160S2. Очевидно, что возможности экономии снижаются при увеличении момента нагрузки и уменьшении скорости. В точке Мс = 0,05Мном, со =соном можно дополнительно сберечь 3,6 % номинальной мощности. Если сравнить мощность, потребляемую в данном режиме до и после
1.4 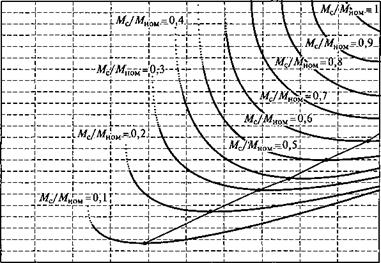
|
|
|
° 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Ui/UHOU а |
|
° 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 tycoon б |
|
Рис. 4.2. Зависимость потерь АР в АД типа 4A160S2 от амплитуды напряжения при постоянной скорости и разных моментах нагрузки при со = — ^ном (^) И 0) — 0,5шном (б) |
|
161 |
6 Браслапский
|
Экономия потребляемой мощности двигателем типа 4A160S2 в зависимости от скорости и момента статической нагрузки, ЛР/Рном > %
|
введения оптимизации, то полученная экономия составит 40 %. Однако выражение экономии потребляемой мощности в процентах от номинальной мощности дает более наглядное, не зависящее от рабочей точки, представление о возможном эффекте.
Аналогичные расчеты были проведены для двигателя типа 4А80А4, имеющего Рном =1,1 кВт. В точке Мс = 0,05Мном, со =соном можно сэкономить до 13 % номинальной мощности. При расчете в
|
|
|
Рис. 4.3. Диаграмма экономии потребляемой энергии двигателем типа 4A160S2 в зависимости от скорости и момента статической нагрузки |
этой же точке для двигателя типа 4АН250М4 (Рном =110 кВт) получено 2,4 % экономии. Это подтверждает известный факт увеличения эффективности энергосберегающего режима с уменьшением мощности двигателя.
Энергосберегающий режим может быть осуществлен следующими способами:
1) поддержанием постоянства coscpb
2) поддержанием постоянного скольжения;
3) управлением с использованием модели двигателя;
4) с помощью поисковых алгоритмов.
Перечисленные способы оптимизации, кроме последнего, используют информацию о параметрах двигателя, которая, как правило, неизвестна. Загружать систему скалярного управления задачами идентификации не представляется целесообразным. Поэтому наиболее надежным и независимым от свойств конкретного объекта управления методом оптимизации являются поисковые алгоритмы, которые при расчете используют только значения токов и напряжений.
В этом случае оптимальный режим достигается путем минимизации потребляемой мощности, рассчитанной по формуле
Рі = Зі/^совф!. (4.9)
В процессе работы система управления итеративно (ступенчато) изменяет уровень напряжения для отыскания точки минимального энергопотребления. Критерием поиска может также служить максимум соБф! или минимум потребляемого тока [74]. Отыскание максимума соБф! не дает преимуществ перед минимизацией мощности с точки зрения вычислительной сложности, так как cos ф рассчитывается также через векторы тока и напряжения. Преимущество в данном случае заключается в том, что максимум С05ф выражен более явно, чем минимум мощности, и он легче локализуется. Недостатком является несоответствие максимального и оптимального созф. Преимущество минимизации тока заключается в упрощении реализации алгоритма. Однако это упрощение несущественно, так как на практике приходится использовать процедуры обработки и фильтрации сигналов с датчиков тока. Дополнительное введение в расчет вектора напряжения не приводит к заметному усложнению, так как можно использовать заданное значение этого вектора при осуществлении векторной ШИМ. Расчет косинусоидальной функции также проводится сравнительно просто даже при использовании относительно несложных микроконтроллеров. Кроме того, регулирование по минимуму тока не соответствует регулированию по минимуму мощности.
При осуществлении энергосберегающего алгоритма возникает проблема снижения перегрузочной способности двигателя при уменьшении напряжения питания. Система управления должна
восстанавливать магнитныи поток при механическом возмущении, т. е. реагировать на увеличение тока. Критический момент в данном случае пропорционален квадрату напряжения [47] и может быть рассчитан по формуле
Таким образом, наиболее приемлемым методом оптимизации энергопотребления для преобразователей со скалярным управлением следует признать метод минимизации потребляемой мощности.
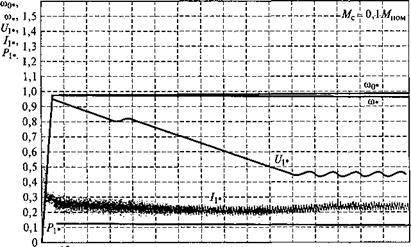
В качестве примера на рис. 4.4 представлены характеристики процесса пуска и поиска оптимального напряжения при работе АД в установившемся режиме при соном (Рх,, Uu, со* и со0* даны в относительных единицах, за базовые величины приняты их номинальные значения).
Поисковому алгоритму может потребоваться несколько десятков секунд для обнаружения оптимальной точки, что делает его непригодным к использованию в механизмах циклического действия с малыми циклами. Это обусловливает целесообразность применения алгоритма поиска минимума потребляемой мощности в электроприводах, длительно работающих с постоянными нагрузками, значительно меньшими номинальных.
|
20 30 40 50 60 70 80 90 100 110 120 130 140 Рис. 4.4. Характеристики процесса поиска оптимального напряжения при работе АД в установившемся режиме при соном |
Турбомеханизмы характеризуются существенным уменьшением момента нагрузки со снижением скорости, что, с одной стороны, является преимуществом с точки зрения устойчивости к снижению перегрузочной способности, а с другой — не позволяет получить высокую эффективность энергосберегающего режима, так как максимум экономии достигается при максимальной скорости и минимуме момента нагрузки.
Как было сказано в гл. 3, возможность снижения напряжения на статоре при снижении нагрузки на двигателе имеется и в системе ТПН—АД.