ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
Плавный пуск в системах ПЧ — АД
Ранее мы отметили, что возросшая необходимость экономии энергии поставила задачу перехода к регулируемому полупроводниковому электроприводу переменного тока. Асинхронный электропривод с частотным регулированием скорости наряду с существенной экономией электроэнергии в статических режимах работы позволяет осуществлять плавный пуск и торможение. Необходимость формирования плавно протекающих переходных процессов в асинхронных электроприводах обусловлена тем, что АД
с короткозамкнутым ротором при прямом пуске, т. е. при подключении обмотки статора непосредственно к источнику номинального напряжения, при частоте 50 Гц имеет не совсем удовлетворяющие требованиям характеристики.
Принципиальной особенностью прямого пуска АД с коротко - замкнутым ротором является возникновение больших электромагнитных моментов и токов. Большие броски электромагнитных моментов могут вызвать опасные динамические нагрузки на обмотки электродвигателей и механические напряжения в элементах кинематической цепи электропривода. Формирование плавных переходных процессов при пуске и торможении обеспечивает исключение больших динамических нагрузок, что увеличивает срок службы электродвигателей и элементов механического оборудования. Кроме того, при большой мощности электропривода благодаря плавному пуску исключается воздействие пиковых электрических нагрузок на питающую сеть, что благоприятно сказывается на других потребителях электрической энергии.
|
|
|
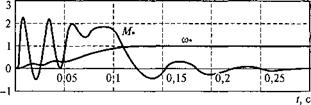
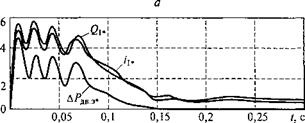
б Рис. 3.51. Переходные процессы АД типа 4А132М6 с короткозамкнутым ротором при прямом пуске Mct = 0 |
На рис. 3.51 приведены зависимости мгновенных значений электромагнитного момента М*(/), угловой скорости со*(/) и тока статора при прямом пуске АД типа 4А132М6, имеющего Рном = 7,5 кВт. При моделировании использовались уравнения (2.27) с учетом нелинейного характера кривой намагничивания по главному магнитному пути. На рис. 3.51, а видно, что переходный процесс по моменту M,(t) носит колебательный характер. Значение первого ударного момента составляет 2,75Мном при токе статора 5,5/1ном. По мере разгона двигателя колебания момента и тока
затухают, а угловая скорость ротора со» приближается к установившемуся значению.
Цифровое моделирование переходных процессов позволяет оценить энергетические показатели асинхронного двигателя при прямом пуске. Практический интерес представляют зависимости суммарных электрических потерь ДРдв. э*(0 и реактивной мощности показанные на рис. 3.51, б. Потери ЛРдВ. э*(0 и мощ
ность Q*(t) даны в относительных единицах, для которых базисной величиной является номинальное значение электромагнитной мощности двигателя. Большие токи статора и ротора в переходном режиме вызывают потери и увеличенное потребление реактивной мощности, в несколько раз превышающие их значения в номинальном режиме двигателя. Так, максимальные потери энергии в переходном процессе превышают номинальную электромагнитную мощность двигателя в 4,8 раза, а максимальная реактивная мощность — почти в 6 раз.
Таким образом, прямой пуск АД сопровождается ударными моментами и токами в обмотках статора и ротора, значительно превышающими номинальные. Из-за этого потери энергии в двигателе и потребление им реактивной мощности при прямом пуске существенно возрастают.
Ударные моменты, пусковые токи, потери мощности и потребление реактивной мощности могут быть снижены в разомкнутых системах управления АД при плавном изменении частоты напряжения статора. При частотном способе управления наряду с другими факторами важную роль играет выбор закона частотного управления. Рассмотрим подробнее формирование плавного пуска и энергетику асинхронного электропривода при частотном способе управления пуском. Задачей исследования поставим выявление качественных особенностей переходных процессов и поведения энергетических характеристик (электрических потерь в сило-
|
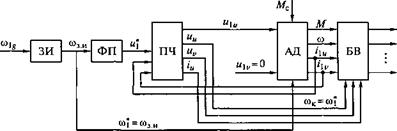
Рис. 3.52. Схема разомкнутой системы управления частотно-регулируемого асинхронного электропривода: ЗИ — задатчик интенсивности; ФП — функциональный преобразователь; ПЧ — преобразователь частоты; АД — асинхронный двигатель; БВ — блок вычисления относительных значений переменных |
вой части и реактивной мощности на входе преобразователя частоты) при частотном пуске двигателя. При управлении переходными процессами частотно-регулируемого электропривода с разомкнутой системой управления возникает необходимость выбора темпа изменения частоты со! для получения плавно протекающих переходных процессов и снижения энергетических затрат. В связи с этим представляет интерес исследование влияния продолжительности изменения частоты со! на характер переходного процесса и энергетические показатели электропривода.
На рис. 3.52 приведена схема разомкнутой системы управления частотно-регулируемого асинхронного электропривода при проведении вычислительного эксперимента. Объектом исследования является разомкнутая система управления электроприводом, в составе которой имеется задатчик интенсивности (ЗИ) и функциональный преобразователь (ФП). При ступенчатом сигнале на входе Wig задатчик интенсивности формирует линейно изменяющийся сигнал задания на угловую частоту сої. Функциональный преобразователь реализует зависимость и = /(сої). Сигналы задания сої и и определяют частоту со, и амплитуду их основной гармоники напряжения статора АД. На выходе системы установлен блок вычисления (БВ) электромагнитного момента, угловой скорости, тока статора, электрических потерь в силовой части и реактивной мощности в относительных единицах.
Математическая модель силовой части электропривода описывается уравнениями (2.27)...(2.30). Для выполнения численных расчетов уравнения (2.27)...(2.29) приведены к системе координат, вращающейся с угловой скоростью результирующего вектора напряжения статора. Система координат ориентирована так, что выполняются условия: сок = сои1 = соь иХи = их, uXv= 0, где
и = УІиІи + uiv — модуль результирующего вектора напряжения. Уравнения (2.30) записаны в системе координат, вращающейся с угловой скоростью результирующего вектора тока (вектора коммутационной функции выпрямителя). При этом составляющие вектора сетевого тока іи = і и iv= div/dt = 0, где і = - Jil + ul — модуль
вектора стока. В принятой системе координат выражения суммарных электрических потерь в силовой части привода и потребляемой из сети реактивной мощности упрощаются и приобретают вид:
3 3
Д^эп. э = ~~ Мсо, Q — ~Uviu.
Для удобства сопоставления результатов расчета абсолютные значения переменных, полученные при решении уравнений модели привода, пересчитываются к безразмерным величинам. Для
|
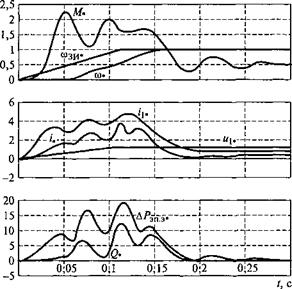
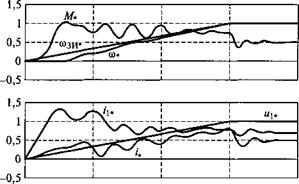
Рис. 3.53. Переходные процессы плавного пуска АД с короткозамкнутым ротором при Л/с* = 0,5Л/ном и Тзи = 0,12 с |
всех переменных, исключая угловую скорость ротора, за базисные единицы принимаются их значения в номинальном режиме работы АД. Для угловой скорости ротора базисной величиной является скорость идеального холостого хода при номинальной частоте напряжения статора.
Исследование процессов, происходящих при плавном пуске АД, Проводилось при линейном изменении ВО времени частоты (Oj = СОТ, которое обеспечивалось задатчиком интенсивности. Одновременно с изменением частоты регулировалось напряжение по закону их/щ = «іномЛ^іном* осуществлявшемуся с помощью ФП.
Результатами расчетов явились представленные на рис. 3.53 переходные процессы плавного пуска АД с короткозамкнутым ротором при Мс = 0,5Мном и Гзи = 0,12 с, а также зависимости во времени электромагнитного момента М*(/), угловой скорости со*(/), тока статора электрических потерь в силовой части АРЭП э*(0 и реактивной мощности Q*{t).
На рис. 3.53 приведены переходные процессы при пуске АД с темпом задатчика интенсивности Тш = 0,12 с, что обеспечивает продолжительность переходного процесса по скорости, примерно равное продолжительности разгона при прямом пуске (см. рис. 3.51). Сопоставляя основные показатели переходных процессов при прямом и частотном пусках АД, можно отметить, что при частотном пуске величина ударного момента уменьшилась и его максималь
ное значение составило 2,2Мном, ток статора снизился до величины, равной 4/1ном, число ударных пиков сократилось в 2 раза, т. е. двигатель разгоняется плавно и выходит на установившуюся скорость с меньшим перерегулированием.
Частотный пуск сопровождается гораздо меньшими энергетическими затратами. Обратим внимание прежде всего на то, что снизились электрические потери в приводе. Максимальное значение мгновенных потерь ДРэп. эЛО при частотном пуске уменьшилось в 1,8 раза по сравнению с прямым пуском. Потери энергии при частотном пуске составили 1760 Дж вместо 3333 Дж при прямом пуске. Особенно показателен эффект от использования частотного пуска по реактивной мощности Q*, потребляемой приводом из сети. При частотном пуске максимальная величина реактивной мощности составляет 12,5QHom (см. рис. 3.53), что в 14,5 раза меньше величины реактивной мощности, потребляемой приводом при прямом пуске. Различен также характер протекания переходных процессов по реактивной мощности. При прямом пуске Q*{t) быстро нарастает на начальной стадии переходного процесса и начинает падать только к концу разгона двигателя. При частотном пуске, как видно из зависимости Q* (/) (см. рис. 3.53), потребление реактивной мощности нарастает медленнее и достигает максимума к середине переходного процесса.
|
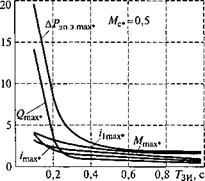
Рис. 3.54. Зависимости максимумов показателей качества от параметра Тзи |
Исследование влияния изменения темпа ЗИ показывает, что при увеличении параметра Тш максимальные значения электромагнитного момента Л/тах*, тока статора /ітах», сетевого тока /тах„, электрических потерь В приводе ДРэп. этах* и реаКТИВНОЙ МОЩНОСТИ 0тах* монотонно уменьшаются, приближаясь асимптотически к своим установившимся значениям. Результаты этого исследования отражены на рис. 3.54 и соответствуют фиксированному значению статической нагрузки Мс* = 0,5 и суммарному моменту инерции привода /= 2/дв. Характер поведения зависимостей на рис. 3.54 говорит о целесообразности увеличения параметра Тш для снижения токов, электрических потерь и реактивной мощности при частотном пуске, если время разгона привода не ограниченно. В этом случае, как видно на рис. 3.54, параметр Тш должен превышать продолжительность разгона АД при прямом пуске /п. п.
Особый интерес представляет зависимость электрических
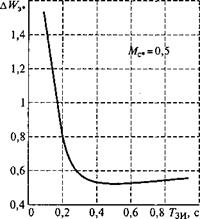
потерь энергии AW3* от параметра Гзи (рис. 3.55), имеющая принципиально иной характер в исследуемом диапазоне изменения Тш. При Тш > /п п функция А РК,*(ГЗИ) минимальна (см. рис. 3.55). Значение параметра Гзи, доставляющее минимальное значение функции ДЖЭ*(ГЗИ), зависит от момента статической нагрузки Мс, и момента инерции привода /. График функции А^э*(7зи) соответствует Мс, = 0,5 и J — 2/дв.
|
Рис. 3.55. Зависимость потерь энергии от параметра Тш при частотном пуске АД |
При сравнительно большой продолжительности развертки ЗИ, превышающей примерно в 2 — 3 раза продолжительность прямого пуска, максимальное значение переходного момента не превышает значения, соответствующего номинальной перегрузочной способности. При этом колебания момента, вызываемые электромагнитными переходными процессами, практически отсутствуют, ротор достигает установившегося значения скорости почти одновременно с окончанием изменения частоты и на протяжении всего процесса разгона точно следует за изменением частоты, что соответствует мягкому режиму частотного пуска. На рис. 3.56 приведены характеристики режима мягкого частотного пуска АД с короткозамкнутым ротором при Мс* = 0,5 и Гзи = 5/п п = с, которое соответствует минимальному значению потерь энергии АЖэ* [см. график функции АЖЭ,(ГЗИ) на рис. 3.55].
На рис. 3.56 видно, что максимальное значение электромагнитного момента равно номинальному моменту двигателя Afmax* = 1. При разгоне пусковой момент практически постоянен. Реальная скорость отслеживает задание, поступающее с задатчика интенсивности, с небольшими колебаниями и скоростной ошибкой и выходит на установившееся значение скорости за период, равный продолжительности развертки Гзи. Пик тока статора снижен до значения 1,38/1ном и большую часть продолжительности разгона остается практически постоянным. Сетевой ток, сохраняя некоторые колебания, возрастает, достигая максимального значения только к завершению разгона двигателя. Потери энергии и реактивная мощность в этом режиме меньше по сравнению с частотным пуском при Тзн = 0,12 с, максимальное значение электрических потерь уменьшается в 10 раз, а потребление реактивной мощности снижается в 31 раз. Сравнение интегральных характеристик показывает значительный выигрыш при использовании
|
|
режима мягкого пуска: при оптимальном параметре Тш = 0,6 с потери энергии за время пуска составляют 625 Дж, что в 2,8 раза меньше потерь энергии при частотном пуске с параметром Тш = 0,12 с.
По мере уменьшения продолжительности Гзи, начиная с Тш = = /п п, наблюдается возрастание бросков электромагнитного момента и значительное увеличение колебаний электромагнитного момента на начальном участке пуска, где угловая скорость ротора еще сравнительно невелика. При этом колебания возрастают по длительности, амплитуде и при малых статических нагрузках появляются отрицательные выбросы момента. Колебания момента особенно сильно проявляются в случае пуска под нагрузкой. Следовательно, с энергетической точки зрения уменьшение продолжительности Тш приводит к снижению положительного эффекта.
Таким образом, простейшие системы управления АД позволяют путем подбора параметра Тш воздействовать на показатели качества переходных процессов электромеханических и электрических координат, а также на энергетические показатели электропривода. Однако в разомкнутых системах проявляется влияние свободных электромагнитных колебаний, что не всегда удовлетворяет требованиям технологических процессов. Кроме того, с точки зрения оптимизации энергетических показателей электропривода в режиме пропорционального управления АД нельзя добиться нужного эффекта в условиях изменения момента нагрузки и при изменяющемся моменте инерции или других параметров двигателя. Заметим также, что оптимальное значение параметра Тш не отвечает решению задачи оптимального управления по минимуму электрических потерь энергии, а является лишь некоторым ее приближением. Более полно осуществить заложенные в способ частотного управления АД возможности удается только в замкнутых системах автоматического управления, построенных с привлечением методов математической теории оптимального управления и методов синтеза многосвязных систем подчиненного регулирования. Рассмотрим некоторые подходы к этой важной проблеме.