ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
Системы ПЧ—АД
Рассмотренные в подразд. 3.1.3 характеристики частотно-регулируемого электропривода относились собственно к асинхронному двигателю. Для полноты оценки свойств системы ПЧ—АД как потребителя электрической энергии в установившемся режиме работы частотно-регулируемого электропривода рассмотрим потребляемую из сети реактивную мощность. Для расчета реактивной мощности на входе ПЧ воспользуемся формулами сетевых характеристик (2.60), полученных в предположении отсутствия высших гармоник в кривых токов и напряжений преобразователя, электрических потерь в вентилях выпрямителя и полупроводниковых ключах автономного инвертора напряжения, а также потерь в стали реакторов. При этих допущениях реактивная мощность на входе ПЧ определяется по формуле
18
Q = — "оэА>.вх42- (3.73)
п1
Формула (3.73) показывает, что реактивная мощность Q зависит от величины выходного тока выпрямителя /в и индуктивного сопротивления Хр вх = щэЬрвх коммутирующего реактора. Ток /в в процессе регулирования скорости и изменения момента нагрузки является переменной величиной. Это означает, что на потребление Q влияет режим работы двигателя, точнее ток статора i{ и активная мощность Рь потребляемые от преобразователя частоты. Ток статора /ь мощность и ток /в связаны уравнением баланса мощностей (см. 2.61) преобразователя частоты, которое для определения тока инвертора преобразуется к биквадратному уравнению
Аі4в + ВіІ + С = 0, (3.74)
где коэффициенты А, В, С определяются из выражений:
На основании формулы (3.73) с учетом уравнения баланса мощностей в преобразователе можно сделать следующие выводы. Реактивная мощность на входе Q и реактивная мощность на выходе Qi преобразователя частоты не равны друг другу. Так как мощность Q определяется при заданных параметрах реакторного оборудования преобразователя током статора и активной мощностью двигателя, то можно предположить, что при регулировании скорости вниз от основной скорости вращения АД реактивная мощность на входе преобразователя будет уменьшаться, а при постоянстве скорости двигателя с увеличением момента нагрузки на валу мощность Q будет возрастать. При этом входная реактивная мощность ПЧ отличается от его выходной мощности при любых знаках Qx и Рх. Мощность Q всегда является положительной, т. е. она потребляется от источника питания выпрямителем.
Ввиду незначительной величины реактивного сопротивления коммутирующего реактора потребление мощности Q при рабочих нагрузках достаточно мало. С уменьшением величины индуктивного сопротивления коммутирующего реактора потребление из сети реактивной мощности уменьшается. При Lp вых —> 0 мощность Q —»0.
Практический интерес представляет оценка влияния закона частотного управления на потребление реактивной мощности Q. При выбранном режиме частотного управления двигателем процедура расчета сводится к следующей последовательности действий. Сначала рассчитывается ток статора и активная мощность двигателя, соответствующие заданным значениям скорости и момента нагрузки двигателя. Для этого используется методика расчета характеристик АД. Затем полученные значения тока ix и мощности Рх подставляются в выражения для коэффициентов В и С биквадратного уравнение (3.74), и из него определяется ток /в. Теперь, зная входной ток инвертора, можно по формуле (3.73) рассчитать потребляемую преобразователем мощность Q. Для других значений скорости и момента процедура расчета повторяется. Для достоверности решения, оценки свойств и возможностей частотно-регулируемого асинхронного электропривода следует учитывать насыщение АД по главному магнитному пути.
На рис. 3.36 и 3.37 приведены зависимости реактивной мощности Q от электромагнитного момента при различных фиксированных значениях угловой частоты напряжения статора. Расчеты выполнены для двигателя типа 4А132М6 в режимах пропорционального управления («і/сої = wlHOM/colHOM) и ПРИ постоянстве полного потокосцепления ротора (|/2 = V2ном)- При построении зависимостей использованы безразмерные величины: реактивная мощность отнесена к номинальной электромагнитной мощности (Q* = Q/P3M. U0M), мо-
|
*м(1) |
|
|
|
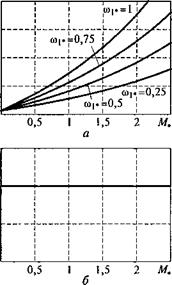
Рис. 3.37. Зависимости реактивной мощности (а) и коэффициента мощности (б) ПЧ двигателя типа 4А132М6 от момента Mt в режиме управления щ = У2ном |
|
Q. 0,03 0,02 0,01 0 *м(1) 1 0,5 0 |
1 -
0,5 -
0,5 1 1,5 2 Л/,
б
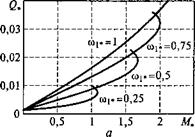
Рис. 3.36. Зависимости реактивной мощности (а) и коэффициента мощности (б) ПЧ двигателя типа 4А132М6 от момента М. в режиме управления и/(йі = W|ном/сО| ном
мент — к номинальному значению момента (М* = М/Мном) и угловая частота — к номинальному значению угловой частоты напряжения (о))* = cO]/cd1hom) двигателя.
Как видно на рис. 3.36 и 3.37, при фиксированной частоте о,* с увеличением момента потребление реактивной мощности увеличивается. После перехода критической точки механической характеристики, несмотря на резкое падение скорости двигателя, потребляемая из сети реактивная мощность в режиме управления Wj/cdj = и і ном/ ^ і ном также возрастает. При фиксированном значении момента с уменьшением частоты coj* потребление реактивной мощности уменьшается. Таким образом, максимум реактивной мощности на входе преобразователя в частотно-регулируемом асинхронном электроприводе при работе его на статически устойчивом участке механической характеристики приходится на точку с максимальными значениями скорости и момента.
Сравнивая потребление реактивной мощности Q при разных законах управления, отметим, что в области рабочих нагрузок, т. е. при А/* < 1, частотно-регулируемый асинхронный электропривод характеризуется достаточно малым потреблением реактивной мощности от источника питания. Для электропривода с двигателем
типа 4А132М6 в указанной области нагрузок она не превышает 2 % номинальной электромагнитной мощности. Сравнительная оценка режимов управления щ/щ = иЫоы/щном и |/у = ц/уном, где у = 0, 1,2, показывает, что графики функции Q*(M») при фиксированных частотах а)!* > 0,5 практически сливаются. Если сох* < 0,5, то предпочтительнее оказываются режимы управления, обеспечивающие постоянство потокосцепления статора, главного потокосцепления, или потокосцепления ротора. Эти режимы управления являются также более эффективными при перегрузках двигателя.
Другим важным сетевым энергетическим показателем частот - но-регулируемого асинхронного электропривода является коэффициент мощности на входе преобразователя. В рамках принятых допущений коэффициент мощности по основным гармоническим составляющим сетевого тока и напряжения
|
(3.75) |
*м(1) = PS'1.
Активная и полная мощности электропривода определяются по формулам:
|
|
|
зТз. |
|
71 |
|
Р = |
|
п |
(3.76)
|
п |
(3.77)
|
|
Из формул (3.75)...(3.77) следует, что при ZpBX = 0 полная и активная мощности равны. В этом случае потребление от сети реактивной мощности отсутствует и коэффициент МОЩНОСТИ £м(1) = 1. Однако на практике из-за наличия конечного индуктивного сопротивления ^Гр ВХ коэффициент мощности £м(1) < 1. Коэффициент мощности &м(1) зависит от момента М и скорости со, а также режима управления двигателем. На значение коэффициента мощности оказывает влияние напряжение и источника питания преобразователя. Подставив формулы (3.76) и (3.77) в формулу (3.75), получим более удобное для расчетов выражение:
(3.78)
Из формулы (3.78) следует, что при заданном значении напряжения и источника питания и индуктивном сопротивлении ^р. вх ф коэффициент мощности /см(1) = 1 только при отсутствии потребления тока /в, а при /в ф 0 с увеличением напряжения и ток /в уменьшается и, следовательно, коэффициент мощности /см(1) увеличивается. Как видно из графиков на рис. 3.36 и 3.37, сетевой
коэффициент мощности в области рабочих нагрузок близок к единице. При перегрузках, а также при малых значениях угловой частоты напряжения статора предпочтительнее использовать режимы управления при постоянстве потокосцепления статора, главного потокосцепления или потокосцепления ротора.
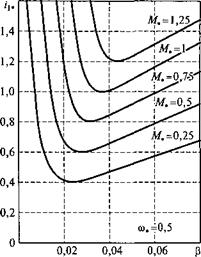
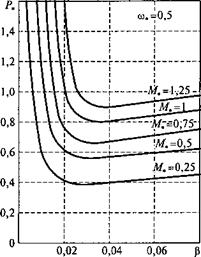
Отметим, что частотно-регулируемый асинхронный электропривод как объект управления обладает экстремальными характеристиками по сетевым показателям. Это вытекает из анализа формул сетевых характеристик электропривода. Действительно, при наличии экстремума тока /в* все они примут экстремальные значения. На рис. 3.38 приведены зависимости токов /Вф и /ь от скольжения при фиксированных значениях скорости (со* = 0,5) и момента (0,25 <М*< 1,25). Функция /В,(Р) имеет минимум (см. рис. 3.38, а). Анализ экстремального по току /в закона управления показывает, что оптимальное скольжение зависит как от момента, так и от скорости двигателя и в общем случае не совпадает при прочих равных условиях со значениями (3 в точках минимума функций мощности потерь и тока статора. Однако режим минимального тока /в, достаточно близок как к режиму минимального тока статора, так и к режиму управления по минимуму полных потерь двигателя. Для сравнения на рис. 3.38, б приведены зависимости тока статора от параметра абсолютного скольжения при различных фиксированных значениях момента. Заметим, что закон оптимального управления по минимуму тока статора не зависит от
|
|
Рис. 3.38. Зависимости токов /в# (а) и /и (б) от скольжения при фиксированных значениях скорости и момента
|
|
|
|
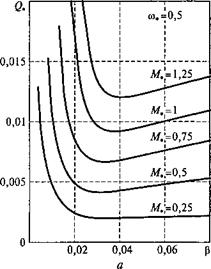
Рис. 3.39. Зависимости реактивной Q„ (а) и активной Рф (б) мощностей от скольжения при фиксированных значениях скорости и момента
скорости двигателя и имеет более ярко выраженный экстремум. Как видно на рис. 3.38, в режиме минимума тока статора практически обеспечивается минимум тока /„*.
При минимуме тока /в<! сетевой ток активная реактивная Q* и полная S* мощности, потребляемые преобразователем от источника питания, будут иметь минимальные значения, а коэффициент мощности &м(1) будет максимальным. На рис. 3.39 приведены зависимости реактивной Q* = Q/P3м ном и активной Р* = Р/Рэм, ном мощностей от скольжения при фиксированных значениях скорости и момента. Как видно на рис. 3.39, функции Qt(Mt, со„, Р) и Р*(М^, (о„, р) имеют явно выраженный минимум при скольжении, соответствующем минимуму тока на входе инвертора.