ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
РЕАКТИВНЫЕ НАПРЯЖЕНИЯ
|
В том случае, если реактивные напряжения стреакт известны, и известна жесткость конструкции dN |
|
du ’ |
|
Ж — |
|
ux (be, t) ux (be, be) |
|
|
|
E Р0' |
|
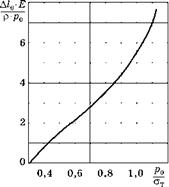
Рис. 7.17 Зависимость упругой податливости Al0 поля собственных напряжений у круглого люка с радиусом р при нагрузке Р0 |
|
= 2 • |
|
(7.24) |
|
250 0,75-24 3,2 • 250 • 0,75 • 24 2,1 104 |
|
откуда |
|
Al0 - |
где N — усилие; и - перемещение конструкции в рассматриваемом месте, упругую податливость можно вычислить по простой формуле
|
|
(7.25)
где F1 — площадь поперечного сечения элемента конструкции, в которой действуют реактивные напряжения.
Если реактивные напряжения вызваны сваркой, то А1с можно считать равной сварочной деформации от последнего шва, замыкающего конструкцию. Обычно это поперечный стыковой шов. Поперечные деформации такого шва могут быть вычислены по формуле
где а и су — коэффициент линейного расширения и объемная теплоемкость стали; 1ш и F1 — длина сварного шва и площадь сечения свариваемого элемента конструкции; qп — погонная энергия сварки; m — коэффициент, зависящий от условий сварки.
При электрошлаковой сварке очень крупных пластин он достигает 1,6. При сварке крупных полотнищ автоматической сваркой m = 0,8-1,2. При сварке в жестком закреплении короткими швами m ~ 0,3.
Для многопроходных швов нужно учитывать влияние наложения упругопластических полей от сварочных деформаций.
Для ручной дуговой сварки поперечного многопроходного шва по F-образной разделке с углом раскрытия р можно получить следующую формулу:
|
|
где ид — напряжение дуги; ан — коэффициент наплавки; А — толщина металла; n — количество проходов.
Попробуйте построить подобную формулу, например, для X - образной разделки.
Обычно поперечные деформации даже однопроходного шва составляют порядка 1 мм. Поэтому при отсутствии дополнительных сведений нужно считать, что для реактивных напряжений Д10 > Д1кр, и реактивные напряжения суммируются с напряжениями от внешней нагрузки.