ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ

УЧЕТ ПЕРЕРАСПРЕДЕЛЕНИЯ СОБСТВЕННЫХ НАПРЯЖЕНИЙ

Предположим, что в процессе снятия собственных напряжений при увеличении Aly(y) закон распределения стсб(у) не меняется. То­гда распределение собственных напряжений может быть задано формулой стсб(у) = A ■ f(y). На рис. 7.6 f(y) — ступенчатая функ­ция, два раза переходящая через 0. Она не изменяется в процессе

перемещения границ упругопластической зоны. Изменяется толь­ко множитель A, задающий высоту эпюры асб(у). Обозначим макси­мальную величину собственных напряжений в исходном состоянии (до нагружения конструкции) через ссб, 0.

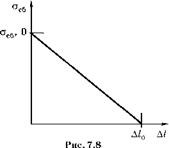
Задача, нарисованная в левой части рис. 7.6, упругая (линейная). В такой задаче перемещения линейно связаны с нагрузками. Зна­чит, зависимость оставшихся максимальных собственных напря­жений от перемещений Al будет такой, как показано на рис. 7.8.

При нулевых перемещениях гра­ницы величина собственных напря­жений равна начальной, а при Al = = Al0 - 0. При промежуточных зна­чениях Al величина собственных на­пряжений выражается формулой

°сб =°сб, о 'f1 j, (7.13)

которая справедлива только для иде - Линейное снятие ального случая, когда функция f(y)

собственных напряжений не изменяется. В действительности

пластические деформации в наибо­лее слабых (где дефект) и в наиболее нагруженных (опасных) мес­тах зоны разрушения будут больше, чем в соседних. В этом случае снижение собственных напряжений в опасных местах будет про­исходить быстрее, чем это следует из рис. 7.8 и приведенной выше формулы. Тогда в общем случае формулу (7.13) нужно переписать в виде

^сб ^^сб о 'I 1 —гг-I. (7.14)

Если эту формулу отнести к моменту разрушения, то Al будет в этот момент равно критической деформации для зоны разруше­ния А1кр. Поэтому еще раз перепишем формулу для зарождения разрушения: f Al Л

°сб-°сб,° У 'А^} (7.15)

Обратимся к силовому критерию разрушения. Металл «не зна­ет», какие напряжения его растягивают — собственные или от внешней нагрузки, и при разрушении реагирует только на сумму всех действующих в нем напряжений. Поэтому если собственные напряжения не сняты полностью, то вторую формулу (7.12) нуж­но записать в видеp + ссб < скр.

Чтобы вычислять безопасный уровень номинальных напряже­ний, в указанной выше формуле нужно собственные напряжения перенести в правую часть и подставить вместо них правую часть формулы (7.15):

( А1кр)

Р ^°кр -°сб,0 I1 —^J - (7.16)

Если речь идет о разрушающих напряжениях от полезной нагруз­ки, то знак неравенства в формуле (7.16) нужно изменить на противо­положный. Разрушающее значе­ние p будет обязательно больше, чем дает правая часть формулы (7.16).

На рис. 7.9 формула (7.16) пред­ставлена графически.

Вертикальная прерывистая ли­ния соответствует верхней крити­ческой температуре Тквр рис. 7.3.

Справа от этой линии сопротивле­ние материалов работает, и ника­ких собственных напряжений учи­тывать не следует; слева — нет, и требуется учитывать собственные напряжения.

В этой зоне напряжения не должны превышать уровня наклон­ных линий, которые проведены для различных значений началь­ных собственных напряжений. Если начальных напряжений нет (стсб, 0 = 0), то методы расчета по сопромату справедливы в преде­лах всего графика. Максимальные значения собственных напря­жений ограничиваются прочностью зоны разрушения. Поэтому в нижней правой части графика, ограниченной косой штриховкой, работоспособность сварной конструкции гарантирована.

Точка графика, в которой А1кр/А10 = 0, соответствует нижней критической температуре Т^р рис. 7.3 или переходной температу­ре нулевой пластичности Тнп, вычисления которой были приведе­ны в разделе 6. Ниже этой температуры при нагружении конст­рукции не происходит никакого перераспределения собственных напряжений. Здесь собственные напряжения полностью сумми­руются с напряжениями от внешней нагрузки и критерий разру­шения имеет вид:

Р = сткр - °сб, 0. (7.17)