ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
МАЛОЦИКЛОВАЯ УСТАЛОСТЬ
6.4.2.1.
КРИВЫЕ ЦИКЛИЧЕСКОГО НАГРУЖЕНИЯ МАТЕРИАЛА
Микромеханизм разрушения стали при малоцикловой усталости аналогичен механизму вязкого разрушения. В процессе пластической деформации поры зарождаются, накапливаются и сливаются, образуя трещину. Как и при вязком разрушении, этот процесс определяется накоплением интенсивности ві пластической деформации elp, которая не имеет знака. Но в отличие от вязкого разрушения, пластическая деформация при малоцикловой усталости циклическая. Поэтому процесс малоциклового разрушения должен контролироваться суммой приращений Aeip, накопленной в процессе нагружения. Чтобы представлять, что такое Aelp, нужно подробнее рассмотреть кривые нагружения стали при статической и циклической деформациях.
Построим кривые нагружения для стали 22К, подвергнутой нормализации и отпуску. В табл. 1 монографии Н. А. Махутова «Деформационные критерии разрушения» для этой стали приведены значения механических свойств, указанные в первых 5 колонках табл. 6.8.
Таблица 6.8
|
Механические свойства стали 22К
|
Интенсивность пластической деформации при разрушении eklp (6-я колонка таблицы) вычислена по формуле (2.29):
ep=%,p =ln (£ )=ln (§)=in [ (6.145>
где lk — конечная длина, Fk — конечная (в момент разрыва) площадь образца для испытаний на разрыв с начальной длиной l0, начальной площадью F0; у — относительное сужение.
Но характеристика Sh (конечная прочность), приведенная в 3-й колонке таблицы, представляет собой средние напряжения в шейке образца. Интенсивность напряжений в момент разрыва ак1, помещенная в 7-ю колонку таблицы, вычислена по Бриджмену с учетом влияния радиуса шейки цилиндрического образца по первой формуле из (5.45):
Sk
• <6Л46)
где
|
л= f = 0,46 (eihp -0,1). |
a
R
Для того чтобы вычислить модуль упрочнения A и показатель упрочнения n, сначала следует записать три уравнения степенного закона упрочнения для трех известных по табл. 6.8 точек кривой упрочнения:
CT02 = A■ 0,0°2n; ств = A^exn<1)j ; Vik = A■ еПр. (6.147)
Затем исключили из них неизвестную А• поделив одно уравнение на другое, и перенесли все члены в правую часть. В результате получили три разных уравнения для вычисления членов вектора n показателя упрочнения:
F1(”>-(exp(1)n0,002J -0 "о - r»»t[^l(n),n];
°ki ( eki
F2(n)-^-їдаJ-0 "1-root[F2(n),n];
F3(n) -^- - (eki'exp(1)) - 0, n2 - root[F3(n), n].
oB V n J
Три значения вектора модуля упрочнения A можно найти, подставив в уравнения (6.147) полученные значения показателя уп-
рочнения: n1
Л _ СТ02 . A =_ ( exp(1) I. A = °Ы
A 0,002n0; 1 B [ n1 J ; 2 є"2
Откуда следует, что
n0 = 0,177; n1 = 0,173; n2 = 0,176; n = 0,176;
A0 = 870,9; A1 = 869,8; A2 = 870,6; A = 870,4 МПа.
Совсем небольшое различие цифр членов векторов n и Aj свидетельствует о том, что исходные данные хорошо соответствуют степенному закону нагружения со средним значением модуля упрочнения A = 870,4 МПа и средним значением показателя упрочнения n = 0,176, которые приведены в 8 и 9 колонках табл. 6.8.
Построить график кривой нагружения можно из следующих соображений. Интенсивность напряжений связана с интенсивностью пластических деформаций степенной зависимостью = A ■ (eip)n,
откуда можно вычислить интенсивность пластических деформаций eip = (ol/A)1/n. Упругие деформации вычисляются по закону Гука eie = o/E. Следовательно, полные деформации связаны с напряжениями формулой
|
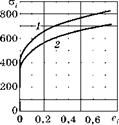
Рис. 6.66 Кривые статического (І) и циклического (2) нагружения |
1/n
|
(6.148) |
ei = ~i + 1 E
Вычисленная по этой формуле кривая показана на рис. 6.66 линией с цифрой 1.
При циклической нагрузке циклически стабильных материалов первые примерно 10 циклов нестабильны. Далее устанавливаются циклический модуль упругости, обозначим его E1, и циклический модуль упрочнения, обозначим его А1, которые примерно на 10% ниже, чем соответствующие статические величины. Тогда кривая циклического нагружения может быть вычислена по формуле
|
1/n |
|
e. = - P - + ei E1+ |
|
Pi A1 |
|
(6.149) |
где E1 = 0,9E; A1 = 0,9A.
На рис. 6.66 кривая для циклического нагружения отмечена 2.
Для построения серии петель циклической нагрузки зададим вектор из четырех значений амплитуд полных (так как в эксперименте пластические деформации не измерить) деформаций:
ea = [0,002; 0,004; 0,006; 0,008].
Поставив эти значения в левую часть выражения (6.149), вычислим соответствующий вектор циклических амплитудных напряжений:
оа = [243,6; 304,6; 337,3; 360,2] МПа.
Кривые циклического нагружения можно построить в MathCad как функции от параметра i = 0,1...200 (номер точки на графике) и параметра j = 0,1...3 (номер кривой). Кривые нулевого нагружения на MathCad могут быть построены с использованием выражений:
|
1/П |
°°(i, i):=OV 2оо;
|
(6.150) |
е0М:=ЯМ* [ ОМ
Кривая циклической повторяющейся деформации с упругой разгрузкой от напряжений - ста до нуля и последующей упругопластической нагрузкой до напряжений <за (при смещении нуля в точку перемены направления нагрузки) выражается формулами:
|
200’ |
S(j, i):=2 ■ aaj
|
S(j, i) - aaj A1 |
|
i < 100,0, |
eS(j, i):=SM+if
Первый и любой нечетный полуцикл нагружения описываются формулами:
a1(j, i):=CTarS(j, і);
e1(j, i):=eaj-eS(j, i). (6.151)
Второй и любой четный полуцикл нагружения описываются формулами:
a2(j, i) := - CTaj + S(j, i);
|
(6.152) |
e2(j, i) := - eaj + eS(j, i).
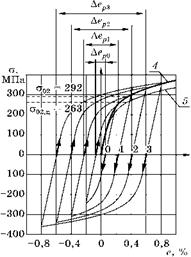
По формулам (6.151) и (6.152) на рис. 6.67 построены четыре (0, 1, 2 и 3) петли циклической деформации для стали 22К при амплитудах деформации, заданных в векторе ea.
|
Рис. 6.67 Статическая (5) и циклическая (4) диаграммы и 4 петли жесткого нагружения стали 22К |
Из рисунка видно, что при жестком нагружении с симметричным циклом и 10% - ном снижении прочности при переходе от статической деформации к циклической вычисленные точки начала нечетных ветвей деформации лежат очень близко к кривой 4 статического нагружения, вычисленной по формуле (6.148), но может быть, это случайное совпадение.
Кривая 5 циклического нагружения, вычисленная по формуле (6.149), проходит ниже.
Кроме этого на рисунке показаны уровни условных пределов текучести для статической ст02 и циклической ст02, ц кривых нагружения.
Шириной петли пластической деформации Авр называется максимальное расстояние между ветвями нагрузки и разгрузки. Связь ширины петли с амплитудой напряжений оа можно получить из степенного закона нагружения:
Аер=fe Г • <6л53>
За каждый полуцикл материал получает приращение наклепа на Авр. Следовательно, за один цикл пластическая деформация прирастает на 2Авр. Но так ведут себя только циклически стабильные материалы.
Как было указано, максимальные напряжения при малоцикловой усталости обычно превышают предел текучести. Так как расчеты на прочность требуют, чтобы номинальные максимальные напряжения были бы ниже предела текучести, то в правильно рассчитанных конструкциях малоцикловая усталость под действием номинальных (расчетных) напряжений невероятна. Она может происходить только в местах концентрации напряжений под действием местных напряжений.
Для приближенного вычисления размаха деформаций в этих условиях можно воспользоваться формулой <3.58) Нейбера. Тогда:
Авр =Авн • ke= <,max ECTmin). k! L, <6.154)
где Авн — размах номинальных (вычисленных по сопромату) деформаций; <rmax, <rmin — номинальные максимальные и минимальные напряжения цикла в опасной точке; k1 — теоретический коэффициент концентрации <полученный в результате упругого решения задачи); ka — упруго-пластический коэффициент концентрации напряжений. Если он неизвестен, то в запас прочности принимают ka =1.