ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
РАЗРУШЕНИЕ ПОЛИКРИСТАЛЛА
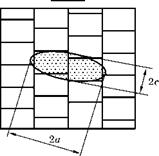
Для прояснения сути вопроса рассмотрим поликристалл, состоящий из кубических зерен (рис. 6.36).
Он растягивается напряжениями S > стс, поэтому отдельные, наиболее благоприятно ориентированные зерна хрупко разрушаются. Трещины, расположенные случайным образом, показаны заштрихованными прямоугольниками.
|
2 = d2, |
Если оценивать эффективный размер этих трещин в соответствии с линейной механикой разрушения, то квадратную трещину можно заменить на круглую той же площади с радиусом а: п - а откуда радиус а этой круглой трещины:
d
а =
-/я
Коэффициент интенсивности напряжений для эллиптической трещины, при с = а, по формуле (3.83), с учетом формулы (6.84):
' Р ■'[а
(6.95)
|
Ф |
|
По 1-І
|
Рис. 6.36
Схема разрушения поликристалла с кубическими зернами
а коэффициент ^-тарировки по формуле (3.84):
Y5 = Я = 0,636.
Следовательно, эффективная длина дефекта а составит:
|
(6.96) |
а = а • Y2 =d• 4 = 0,229 • d.
S к2
Как показывают исследования поверхностей изломов при хрупком разрушении, трещины чрезвычайно редко проникают из одного зерна в другое. Это бывает только в случае, когда кристаллические решетки соседних зерен разориентированы лишь по углу наклона.
Каждое зерно разрушается исключительно по плоскости основания объемно центрированной кубической решетки. Поэтому, если есть винтовая разориентировка этих решеток, то излом, проникший из первого зерна во второе, должен иметь там массу ступенек. Это энергетически крайне невыгодно. Вот почему на схеме (рис. 6.36) предполагается, что трещина останавливается на границе зерна и в соседнее не проникает, где трещина возникает из своего источника и располагается в другой плоскости.
Наиболее слабым местом показанного кристалла является то, где случайно лопнули два соседних зерна. Но чтобы объединить трещины в двух соседних зернах нужно разрушить вертикальную перемычку высотой h, показанную на рисунке. Эта перемычка работает на сдвиг, и возможно только вязкое разрушение. Но высота перемычки h существенно меньше диаметра зерна d. Кроме того, сопротивление металла сдвигу существенно меньше критического напряжения стс, вызывающего раскалывание зерен. Поэтому влияние прочности перемычки на критические напряжения S, разрушающие поликристалл, может быть невелико.
На сечении I-I (рис. 6.36б) эта пара разрушившихся зерен показана в плане заштрихованными квадратами. Влиянием перемычки пренебрегаем. Обычно такие дефекты сложной формы при расчетах заменяются эквивалентным эллипсом. Такой эллипс с полуосями а и с * 2а показан на рис. 6.3.76. Из равенства площадей эллипса и двух квадратов имеем:
п-а - а = п-а -2а = 2 - d2;
|
|
Видно, что при разрушении второго зерна размер малой полуоси эллипса не меняется. Коэффициент интенсивности напряжений, рассчитанный по формулам (3.84), составляет:
|
8 - |
p--/n-a |
|
п- |
3 + |
|
22 |
|
3,25-п |
|
К - |
|
Ф |
следовательно, коэффициент К-тарировки:
8
|
Y5 =- |
- = 0,784.
3,25-л
|
(6.97) |
Эффективный размер дефекта в этом случае: a = a ■ Y52 =-d. 0,7842 = 0,346d.
Л/Л
|
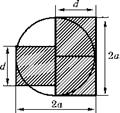
Рис. 6.37 Эффективный размер трещины при разрушении трех соседних зерен |
|
#■ d - л |
|
• = 0,396d. |
|
(6.98) |
|
Сравнение формул (6.96) и (6.97) показывает, что у двух лопнувших зерен эффективный размер трещины в 1,5 раза больше, чем у одного лопнувшего зерна. На рис. 6.37 показана схема разрушения трех наиболее близких соседних зерен. Если их заменить эквивалентным круглым дефектом равной площади, то радиус такого дефекта будет ^ d |
|
a эффективный размер: 4 |
|
a = #■< V л |
|
a = a ■ Y52 = |
|
2 |
От третьего зерна увеличение эффективной длины дефекта составляет только 14%.
Таким образом, можно прийти к заключению, что, если одно зерно не вызывает разрушения поликристалла, то критическим является разрушение двух соседних зерен.
Если первое разрушившееся зерно, наверное, является наиболее крупным и наиболее благоприятно ориентированным, и для него критическое напряжение ас вычисляется по формуле (6.94), то соседнее зерно наверняка не так хорошо ориентировано и может иметь меньший диаметр. Поэтому критическое напряжение Бс, при котором происходит разрушение поликристалла, должно содержать
статистический множитель Ф >1. Кроме того, трудно ожидать, что хрупкое разрушение монокристалла очень большой величины происходит при нулевых напряжениях. Должно существовать некоторое напряжение S0, ниже которого даже очень крупнозернистый материал не разрушается. Тогда для критического напряжения, при котором разрушается поликристалл, формула должна иметь
|
вид |
Sc — S0 +®-ctc — S0 +Ф--^.
c 0 c 0 Vd
Мы вслед за А. Ф. Йоффе назвали это критическое сопротив-
ление поликристалла хрупкому разрушению «сопротивлением отрыву» и обозначили 5отр. Эмпирическая формула для его вычисления имеет вид
|
|
(6.99)
где
|
|
— постоянная материала.
Из формулы (6.99) видно, что в сопротивление отрыву входят только практически не зависящие от температуры или скорости нагружения параметры материала:
у — энергия поверхностного натяжения, зависящая от температуры так же, как и модуль упругости;
E — модуль упругости, практически не зависящий от температуры;
k — коэффициент формулы Петча для предела текучести, тоже практически не зависящий от температуры;
Ф, X и d — геометрические параметры, которые не могут зависеть от температуры.
Независимость 5отр от температуры и скорости нагружения впервые была обоснована экспериментально на кристаллах каменной соли A. Ф. Йоффе, М. В. Кирпичевой и М. А. Левицкой в 1924 г. Однако для поликристаллической стали это удалось показать только через 40 лет. Дело в том, что из-за коррозии на воздухе на поверхности кристаллов каменной соли в микроскоп наблюдаются поверхностные микротрещинки. Условие распространения этих микротрещин по Гриффитсу и позволило сформулировать представление о сопротивлении отрыву, как о критическом напряжении по Гриффитсу, при котором эти трещины распространяются. Но в зернах железа и стали такие микротрещинки никто не видел. Как было изложено выше, они принципиально ненаблюдаемы.
Представить механизм их образования можно только на основе теории дислокаций, а она появилась после 1950 г., когда был построен электронный микроскоп.
|
С отр.» 2 кГ/мм |
|
|
|
100 |
|
50 |
|
0 2 4 6 8 |
|
1/yld, мм ’ |
|
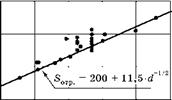
Рис. 6.38 Зависимость сопротивления отрыву от диаметра зерна феррита для сталей |
|
0 |
На рис. 6.38 приведены экспериментальные точки определения сопротивления отрыву 14 различных перлитных конструкционных сталей и феррита в 26 различных состояниях в зависимости от диаметра зерна феррита d.
По нижней границе полосы разброса проведена расчетная прямая, соответствующая формуле (6.99). Из рисунка видно, что в случаях, когда нет никакой дополнительной информации, сопротивление отрыву конструкционных сталей с некоторым запасом прочности можно вычислять по формуле
Ботр = 20 + і!5 кГ/мм2, (6.100)
Vd
где d — диаметр зерна в мм.