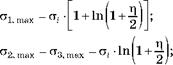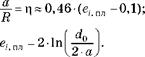ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
Температурные’ зависимости МОДУЛЯ УПРОЧНЕНИЯ И ПОКАЗАТЕЛЯ УПРОЧНЕНИЯ
Для того, чтобы определить по результатам растяжения гладкого образца параметры кривой нагружения (A и n), экспериментальную кривую нагружения (ст; - ег ) строят по точкам в логарифмических координатах, как показано на рис. 5.26.
В качестве исходной используют диаграмму, записанную испытательной машиной в координатах нагрузка — удлинение образца в сумме с деформацией испытательной машины (рис. 5.27).
|
Рис. 5.26 Кривые нагружения образцов в логарифмических координатах и схема определения размеров шейки образца |
|
Р, |
Поскольку в литературе при обработке таких диаграмм часто встречаются ошибки, опишем процесс построения более подробно.
|
1 3 5 7 9 11 ft &[ Рис. 5.27 Обработка машинной диаграммы растяжения гладкого образца |
Точки, относящиеся к площадке текучести, не строят. Для точек, относящихся к возрастающей части кривой нагрузка — удлинение, напряжения и деформации определяются обычным путем:
|
|
(5.42)
где L0 — начальная длина рабочей части образца (L0 = Ьц - D0); Ьц — длина цилиндрической части образца (расстояние между галтелями); D0 — начальный диаметр рабочей части образца; ALra — пластическое удлинение образца, измеряется по диаграмме, записанной машиной; P — нагрузка на образец, измеряется по диаграмме; F — текущая площадь поперечного сечения образца; F0 = nD02/4 — начальная площадь поперечного сечения рабочей части.
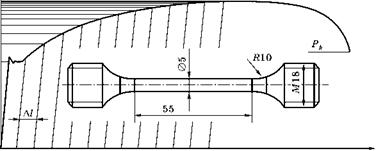
Но как только нагрузка достигает максимума, на рабочей части образца появляется шейка, и в дальнейшем пластические деформации сосредотачиваются в ней. Первая формула (5.42) становится несправедливой, и чтобы далее измерять деформацию, нужно прервать дальнейшее растяжение образца, а в месте ясно видимой шейки поставить датчик, измеряющий диаметр шейки 2а. Если такого датчика нет, приходится ограничиться только вычислением конечной точки диаграммы, предварительно измерив диаметр шейки после разрушения образца и сняв с конечной точки диаграммы значение нагрузки Pk в момент разрушения.
На падающей части кривой нагружения деформации ei определяют по формуле
|
|
(5.43)
где Dmin — минимальный по длине рабочей части образца диаметр в данный момент времени.
Вторая формула (5.42) позволяет вычислить только средние напряжения в минимальном сечении осесимметричного концентратора, которым является шейка на образце. Для вычисления напряжений в шейке можно воспользоваться решением Бриджмена.
Обозначим:
|
|
(5.44)
где а — радиус минимального сечения шейки (рис. 5.266); R — радиус кривизны шейки в минимальном ее сечении (рис. 5.266); S — среднее напряжение в минимальном сечении (S = P/F).
|
S
|
В соответствии с решением Бриджмена, напряжения в минимальном сечении шейки вычисляются по формулам:
(5.45)
Здесь г, ф — полярные координаты в минимальном сечении с радиусом а (рис. 5.266).
Как видно из этих формул, интенсивность напряжений распределяется равномерно по минимальному сечению шейки образца. Касательные напряжения в этом сечении, в силу симметрии верхней и нижней части образца, равны нулю. Поэтому нормальные напряжения и есть главные. Они максимальны на оси вращения образца при г =0. Здесь:

|
|
|
а1, max + 2 ' а2, |
|
|
|
, max |
|
3 |
(5.46)
|
|
Для того чтобы вычислять напряжения по формулам (5.45) и
(5.46) , нужно в процессе испытаний измерять не только диаметр шейки 2а, но и ее радиус кривизны R. Но измерить Rочень непросто. Путем обработки многочисленных результатов измерений, выполненных Бриджменом, получены эмпирические формулы, связывающие параметр ^ с деформацией в шейке образца:
(5.47)
Они позволяют в процессе испытаний обходиться только измерениями диаметра шейки образца.
|
/ 2 КГС/ММ |
|
|
|
120 |
|
100 |
|
80 60 -200-160-120 -80 -40 0 °С Рис. 5.28 Температурные зависимости модуля упрочнения А и показателя упрочнения n стали М16С |
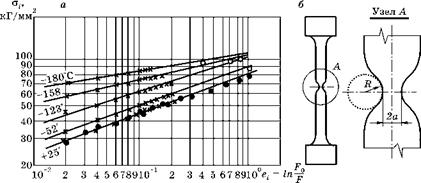
На рис. 5.26а показаны в логарифмических координатах 5 построенных таким образом диаграмм растяжения гладких образцов. Над каждой линией указана температура (°С), при которой производились испытания.
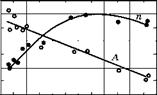
По такому рисунку для каждой кривой нагружения можно определить модуль упрочнения A как ординату точки прямой с абсциссой et = 1,0 и показатель упрочнения n как тангенс угла наклона соответствующей прямой. На рис. 5.28 точками показаны результаты вычислений А и n для стали М16С при различных температурах.
Видно, что модуль упрочнения A практически линейно возрастает с понижением температуры. Показатель упрочнения n при температуре ниже -60°С уменьшается с уменьшением температуры, однако эта зависимость нелинейная.
Итак, чтобы найти упрочнение Астн от предварительного наклепа на величину деформаций ег, н, нужно найти А и n для рассматриваемой стали при той температуре, при которой производился наклеп. Если ег, н < sL, то упрочнение вычисляется по формуле
Л^н = A • еПпл -°т. (5.48)
Если предварительная деформация меньше sL, то приходится считать, что Астн = 0.