ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
РАЗМНОЖЕНИЕ ДИСЛОКАЦИЙ
4.2.8.1.
ИСТОЧНИК ДИСЛОКАЦИЙ И КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ ДЛЯ ЕГО ОТКРЫТИЯ
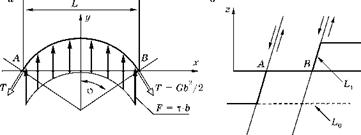
На рис. 4.14а показан закрепленный в точках A и B участок краевой дислокации.
Допустим, что лишняя плоскость вставлена сверху, вектор Бюргерса положителен и направлен вдоль оси у. Точки закрепления могли возникнуть в результате того, что при своем движении дислокация натолкнулась на два твердых неметаллических включения, либо в результате поперечного скольжения, как показано на рис. 4.146 — соседние с точками закрепления A и B участки линии дислокации переместились в другие плоскости. Тогда
|
|
|
а |
|
L |
|
б |
|
I |
|
II |
|
х |
|
Рис. 4.14 Изгиб закрепленного в двух точках участка краевой дислокации распределенной силой F = т ■ Ь |
первоначально прямой край лишней полуплоскости L0, лежащей на осях (zx) и показанной прерывистой линией, в результате поперечных сдвигов по плоскостям I и II приобретает ломаную форму L1, показанную на рисунке жирной линией. Точки А и B оказываются закрепленными при попытке сдвига в плоскости (xy).
Если к первоначально прямому участку дислокации AB приложить распределенную силу F = т - Ь (см. формулу 4.22), то линия дислокации прогнется по дуге окружности с радиусом R и углом 2ф, как показано на рис. 4.14а. Этому изгибу сопротивляется сила линейного натяжения дислокации T = G - Ь2/2 (см. формулу 4.21).
Радиус R можно определить из условия равновесия проекций на ось у всех сил, приложенных к этому участку дислокации:
£ Y = F • L - 2 • T • sin(9) = 0;
х-Ь • 2R• sin(9) -2 •G•b • sin(9) = 0, 2
откуда приложенное напряжение:
Из рис. 4.14а видно, что по мере увеличения прогиба радиус R дуги линии дислокации будет уменьшаться. В соответствии с формулой (4.27) напряжения при этом будут увеличиваться, но только до тех пор, пока линия дислокации не станет полуокружностью с радиусом R = L/2. При дальнейшем увеличении прогиба радиус R начнет увеличиваться, и напряжения т будут падать.
Следовательно, критическое напряжение тс для закрепленного участка дислокации длиной L составляет
|
|
(4.28)
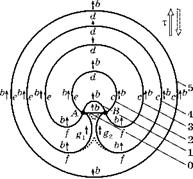
На рис. 4.15 показана схема последовательного положения дислокации в различные моменты времени, которые обозначены справа цифрами от 0 до 5.
|
f Рис. 4.15 Схема шести последовательных положений дислокации при работе источника Франка-Рида |
0 — исходное положение закрепленного участкаАВ дислокации. Линия краевой дислокации прямая, с вектором Бюргерса b, который показан стрелкой, перпендикулярной к линии дислокации АВ.
1 — напряжения близки к критическим (тс = G ■ b/L). Дислокация выгнута по дуге полуокружности с радиусом R = L/2, где L — расстояние между точками закрепления. Положение дислокации соответствует положению, показанному на рис. 4.14а.
2 — под действием силы F =
= т ■ b, приложенной к дислокации, она продолжает двигаться,
R при этом увеличивается. Необходимые для движения напряжения т = G ■ b/(2R) уменьшаются.
Если приложенные напряжения остаются постоянными (т = тс), то дислокация на этой стадии должна двигаться нестабильно, с ускорением, тем большим, чем больше ее радиус. Это подтверждается экспериментально звуковыми щелчками, которые генерируют дислокации при пластической деформации материала. Щелчки регистрируются приборами в диапазоне частот порядка нескольких мегагерц (человек слышит звук с частотой не больше 20 килогерц). Амплитуда звуковых колебаний весьма высока, так как связана с локальными перепадами давления порядка теоретической прочности материала (103 кГ/мм2 = 105 атмосфер).
При любом движении дислокации ее вектор Бюргерса в глобальной системе координат остается постоянным, так как первоначально вставленная лишняя полуплоскость не может при перемещении линии дислокации измениться. Поэтому все стрелочки b на рисунке параллельны во всех точках дислокации в любой момент времени. Однако линия дислокации при перемещении поворачивается, и ориентация вектора b в локальных координатах, связанных с линией дислокации, меняется.
Установим правило для локальных направлений вектора b. Предположим, что мы прогуливаемся по линии дислокации
(в момент времени 2) в направлении BcdeA и наблюдаем за вектором Бюргерса.
Если вектор b ориентирован по нашему ходу (точки с), то дислокация винтовая, положительная. Дефект (в виде реза ножницами) вставлен слева, и он будет распространяться вправо, если сдвиг над плоскостью чертежа направлен вверх.
Если вектор Бюргерса b направлен под прямым углом вправо (точки d) — дислокация краевая положительная. Лишняя плоскость вставлена над плоскостью чертежа. Если сдвиг над плоскостью чертежа направлен вверх, то такая дислокация будет двигаться вверх.
Если вектор Бюргерса параллелен нашему пути, но направлен против нашего движения (точки e), дислокация винтовая отрицательная. Дефект в виде надреза ножницами расположен справа от нас. При сдвиге над плоскостью чертежа вверх такая дислокация будет двигаться влево, расширяя область с дефектом.
Если вектор Бюргерса направлен под прямым углом влево (момент времени 3, точки f) — дислокация краевая отрицательная. Лишняя плоскость вставлена под плоскостью чертежа. Если сдвиг над плоскостью чертежа направлен вверх, то такая дислокация будет двигаться вниз.
Если дислокация направлена под косым углом к нашему движению, то ее вектор нужно разложить на краевую и винтовую составляющие и для каждой составляющей отдельно решать вопрос о ее знаке и направлении движения.
В результате изложенных выше правил можно заключить, что в момент времени 2 точки с и e будут двигаться по горизонтали, отдаляясь друг от друга, точка d будет двигаться вверх, а точки А и B будут оставаться неподвижно закрепленными. В результате, в следующий момент времени дислокация займет положение, указанное на рисунке цифрой 3.
3 — на дислокации появились две новые точки f, в которых краевая дислокация отрицательна. В этих точках линия дислокации будет перемещаться вниз, так как лишняя плоскость находится под поверхностью чертежа.
4 — на дислокации появились еще две новые точки g1 и g2, в которых дислокация винтовая. В точке g1 дислокация винтовая и положительная (как в точке с). Разрез ножницами сделан слева, и здесь линия дислокации будет двигаться вправо.
В точке g2 вектор направлен против нашего обхода, как в точке е. Разрез ножницами здесь сделан справа, и дислокация будет двигаться влево. Таким образом, точки g1 и g2 будут сбли
жаться до тех пор, пока не сольются. В момент их слияния винтовые компоненты вектора Бюргерса противоположного знака «аннигилируют», взаимно уничтожаются. Дислокация в точке слияния распадается на две краевые дислокации с противоположными знаками, как показано на рис. 4.15 пунктирными кривыми. Далее краевые дислокации разных знаков отдаляются друг от друга.
5 — исходная краевая дислокация AB вернулась в первоначальное положение, но кроме этого появилась круглая дислокационная петля 5, которая начала неограниченно расширяться. Если приложенное напряжение т не упало, то начнется новый цикл, в котором будет генерирована еще одна такая же петля, которая отправится вдогонку за петлей 5.
|
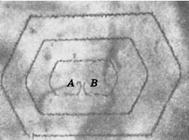
Рис. 4.16 Источник дислокаций в кремнии, декорированный медью |
Форма кривых на рис. 4.15 искажена, она нарисована без учета того, что скорость перемещения участка дислокации в изотропном материале должна быть тем выше, чем больше радиус кривизны R этого участка.
Кроме того, кристаллы металла не изотропны. Это должно привести к появлению углов на петлях дислокаций, подобных тем, что показаны на рис. 4.16.
Здесь сфотографирована дислокация, возникшая из закрепленного участка AB, в положении 4 рис. 4.15 и еще две петли дислокаций, генерированные в прошлых циклах. При оценке этого рисунка следует учитывать, что отдельные дуги дислокаций могли в процессе приготовления шлифа выпрямиться под действием силы линейного натяжения.
Отметим, что во всех рассуждениях этого параграфа не учитывалась сила трения тг, которую необходимо прилагать, чтобы двигать дислокацию по монокристаллу, не имеющему точек закрепления дислокаций. Поэтому указанные на рис. 4.15 напряжения т следует понимать как эффективные:
Teff = т - т;, (4.29)
или как напряжения, перемещающие дислокацию в условиях, когда нет трения (т = 0).