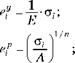ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ СВАРНЫХ КОНСТРУКЦИЙ
ТЕОРИЯ МАЛЫХ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
|
_ 2ii |
Уху |
|
1 3 |
' 2 |
|
= 2iL. |
4yz. |
|
3еі |
' 2 . |
|
І 2 „9 |
у zx |
|
3е, |
2 . |
|
2СТ; . , ' 3e ' (eyy ет); Tyz 2i і 3е_ " (ezz em); ^zx |
При анализе упругопластических задач с концентраторами помимо уравнений равновесия используются физические уравнения, связывающие компоненты девиатора напряжений (аи - стт) и Tjj с компонентами девиатора деформаций (eu - ет) и Уц/2 формулами, аналогичными уравнениям закона Гука. Вместо модуля упругости в этих уравнениях используется отношение 2ст;/3ег:
2СТ; . ,
3е- " xx Єт);
(3.99)
Здесь гидростатические напряжения ат и объемная деформация ет определяются формулами:
_ CTxx + Vyy +
3
ехх + е„„ + czz (3.100)
3
Они связаны друг с другом линейным законом Гука
Е
°т = Т^ЕТ^' ет. (3.101)
Формула (3.101) получается в результате суммирования трех правых частей и трех левых частей трех уравнений линейного закона Гука (3.99).
Интенсивность деформаций et можно представить как сумму интенсивностей упругих деформаций ei и пластических дефор-
|
,p 'і ’
|
|
(3.102) |
маций ep:
где
A — модуль упрочнения материала, равный ст; при деформации ep = 100%; n — показатель упрочнения материала, равный углу наклона диаграммы нагружения материала, построенной в двойных логарифмических координатах [lg(a г), lg(ep)].
Если левые части трех уравнений (3.99) для нормальных напряжений попарно вычесть друг из друга, а уравнения для касательных напряжений поделить на у/2, то можно получить легко запоминающуюся цепочку равенств:
axx - Vyy ®yy - CTzz <Угг - <3ХХ Xxy xyz Tzx _ 2 <3j
xx eyy eyy ezz ezz exx (Ixy/2) (у yz/2) (у zx/2) 3 e ■
Указанная выше система уравнений используется только при численных методах решения задач о концентрации напряжений, например, при методе конечных элементов. Но эти решения по сути представляют численные эксперименты. Их результаты дают только отдельные точки на исследуемых зависимостях. Их нельзя экстраполировать.
При попытках аналитического анализа прибегают к различным упрощениям и гипотезам. Например, при анализе условий зарождения хрупких разрушений, судя по экспериментальным результатам, в первом приближении можно предполагать, что законы распределения напряжений в упругой области минимального сечения у концентратора не изменяются при появлении малой пластической зоны. А в пределах пластической зоны максимальных напряжений Ст! ограничиваются условием текучести: СТ! = л • стт.
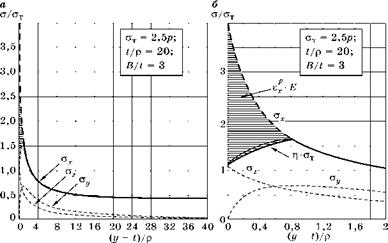
Результаты такого расчета эпюр напряжений в упругопластической области нагружения пластины с центральным отверстием остротой t/p = 20 при относительной ширине пластины B/t = 3 и плоской деформации показаны на рис. 3.45. Рис. 3.45а охватывает всю ширину минимального сечения пластины (2t = 40p). Но в этом масштабе область с высокой концентрацией напряжений
|
Рис. 3.45 Приблизительное распределение напряжений в минимальном сечении пластины с эллиптическим отверстием при упругопластической стадии нагружения |
выглядит очень мелко. Поэтому на рис. 3.456 те же кривые показаны на 1/10 минимального сечения по ширине пластины.
Построение выполнено следующим образом.
1. Задаваясь произвольным значением параметра нагрузки р, например равным 1, по формулам (3.28) были вычислены кривые распределения напряжений (ах, ay и стг) при упругом состоянии материала и плоской деформации. На рисунке эти кривые показаны пунктиром.
2. Задаваясь уровнем напряжений предела текучести, например стт = 2,5р, было построено распределение напряжений в пластической области. Для этого сначала вычислена жесткость напряженного состояния л(у1) по формуле (3.48). Затем эту функцию умножили на отношение напряжений предела текучести к р, т. е. на 2,5. На рис. 3.456 соответствующая кривая обозначена как ^ • стт. Это график распределения максимальных главных нормальных напряжений в упругопластической области (жирная восходящая кривая).
3. Точка пересечения кривых ст1 = ^ • стт и ах при упругом решении соответствует границе упругопластической области, в которой напряжения упругого решения ах (прерывистая кривая) за счет пластических деформаций гХр снижаются до уровня напряжений текучести: ах = ст1т = ^-стт. Зона этих пластических дефор
маций (точнее, зона гХр • E) показана на рис. 3.45 горизонтальной штриховкой.
4. Далее изменили масштаб графика по оси ординат: шкалу а/р разделили на ат/р = 2,5 и получили более понятную шкалу а/ат, которая построена на рис. 3.45.
5. После этого можно найти средние напряженияр0, действующие в брутто-сечении пластины с шириной 2Б:
|
|
где через ут обозначена граница упругопластической области. На рис. 3.456 ут = 0,8р.
Таким образом, эпюра напряжений на стадии локальной текучести в первом приближении построена.
Теперь в нее можно вносить уточнения. Так, можно перейти от плоской деформации к обобщенной плоской деформации, уточнив отношение напряжений р0 по формуле (3.49) с учетом вычисленного выше значения р0, и далее, пересчитав л по формуле (3.48), найти Ст! = л • ат. Это уточнение изменит размер упругопластической зоны ут и р0. Если изменения значительны, придется снова пересчитывать задачу.
Можно учесть, что пластические деформации в зоне, заштрихованной горизонтально на рис. 3.45, происходят без изменения объема. Для них коэффициент Пуассона н = 0,5. Поэтому деформация sz получает дополнительное приращение:
|
Asz =єХ • (0,5-0,3) - |
ASz =Єх • (0,5-0,3) = ^-E:^.0,2,
что приводит к увеличению напряжений az на
ACTz = 0,2(стх - л ат),
где напряжения ах вычислены по формуле (3.28) для упругого поведения материала.
Эта поправка приводит к некоторому повышению жесткости напряженного состояния и повышению напряжений ^ в упругопластической области (исправленная линия а на рис. 3.456 показана тонкой сплошной кривой).
Естественно, что такой анализ пригоден только в пределах локальной текучести и только тогда, когда в упругопластической зоне в направлении осей у и z напряжения с учетом всех добавок не превышают напряжений ах.