ВНУТРЕННИЕ УСИЛИЯ И ДЕФОРМАЦИИ ПРИ СВАРКЕ
Температурное поле при сварке толстых пластин
При сварке пластин толще 50 мм область высоких температур концентрируется вблизи источника нагрева. В отдаленных массах
|
|
металла повышение температуры весьма незначительное. Расчет ведется по схеме нагрева точечным источником полубесконечного тела.
При сварке пластин толщиной 20—50 мм распределение темпе-
стой пластине. источнику нагрева, отличается
от распределения температур в рассмотренных выше плоском и пространственном температурных полях. В этом случае расчет ведут по схеме точечного источника, действующего на поверхности плоского слоя определенной толщины 8 с учетом теплоотдачи от граничных плоскостей.
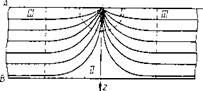
При нагреве точечным источником, движущимся на одной граничной поверхности толстой пластины, различают три области, которые характеризуются неодинаковым распределением температур по толщине пластины (фиг. 4). В области /, прилегающей непосредственно к источнику нагрева, распределение температур по всем трем направлениям примерно такое же, как в полубесконечном теле. В области II в точках, лежащих на оси z и уда-
. 6
ленных от источника нагрева на расстояние z > - у закономерность распределения температур значительно уклоняется от закономерности, наблюдаемой в полубесконечном теле. В области Illy удаленной от оси г, температура по толщине пластины вы - 14
равнивается и напоминает картину плоского температурного поля в тонких пластинах.
В точках, лежащих на оси г, предельная температура по толщине пластины при подвижном источнике нагрева определяется по формуле (5) пространственного температурного поля с поправочным коэффициентом k
VZ
T(-z' V = k (Ц)
|
циента к. |
где k — отношение температуры в точках на оси г толстой пластины к температуре той же точки в полубесконечном теле.
Поправочный коэффициент k зависит от двух без-
размерных параметров и
. Параметр > зависящий
от скорости перемещения источника нагрева, является постоянным для всех точек температурного поля. Другой
безразмерный параметр у-
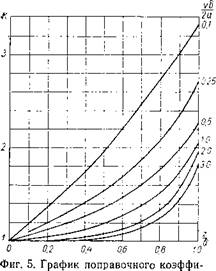
представляет собой относительную глубину расположения точек на оси 2. Значение поправочного коэффициента k в зависимости от обоих безразмерных параметров выбирается по графику, приведенному на фиг. 5.
Из фиг. 5 видно, что в точках, непосредственно прилегающих к источнику нагрева, где 2 = 0, поправочный коэффициент k равен единице и возрастает с удалением от источника нагрева вглубь по оси 2. С увеличением скорости движения источника нагрева поправочный коэффициент k уменьшается, и температура точек на оси 2 толстой пластины мало отличается от температуры этих же точек в полубесконечном теле. Исключение составляет точка 2 = 8, лежащая на нижней граничной поверхности. В этой точке температура превышает в два и более раза температуру точек полубесконечного тела на той же глубине.
Во всех остальных точках толстой пластины (за исключением точек на оси г) предельную температуру можно определить по формуле (1) для линейного подвижного источника с коэффициентом /72.
——
T(r, x,z) = m^r-e 2аКо(Щ, (12)
|
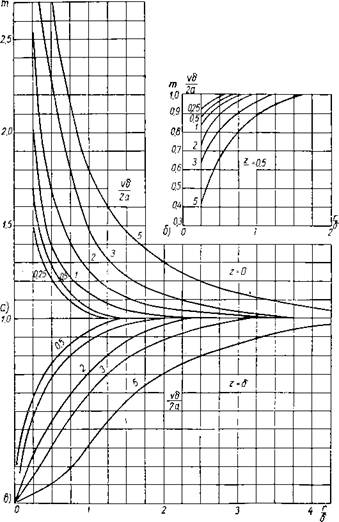
Фиг. 6. График поправочного коэффициента т: |
8
а — нагреваемая плоскость 2— 0; б — средняя плоскость z = —; в — ненагреваемая плоскость z — 5.
где Ко {и) — бесселева функция от мнимого аргумента второго рода нулевого порядка;
г— радиус-вектор плоского поля (г = j/x2 + У2);
/гг — поправочный коэффициент, который показывает отношение температуры в точках толстой пластины, нагреваемой движущимся по верхней поверхности точечным источником, к температуре пластины, нагреваемой линейным источником.
Поправочный коэффициент т зависит от трех безразмерных
vb г z т-г „ а 5
параметров: 2а’ Т И ~ь~' Первый параметр ^ является постоянным для всех точек температурного поля и зависит от скорости движения источника нагрева. Второй параметр у представляет
относительный радиус-вектор точек плоского поля, а третий - у-
является относительной глубиной расположения точек металла 5т$)лстой пластины. Последние два параметра являются чисто геометрическими. Значение коэффициента т в зависимости от указанных трех безразмерных параметров приведено на графике іиг. 6.
.Г Для точек верхней граничной поверхности толстой пластины, эде 2 = 0, коэффициенты т увеличиваются с приближением точек Ж источнику нагрева и уменьшаются с удалением от него, принимая значения, близкие к единице. Для точек, лежащих в
средней плоскости пластины, где г = коэффициенты уменьшаются с приближением к оси 2, а при удалении от нее увеличиваются, стремясь к единице. На нижней граничной поверхности, где 2 = 8, коэффициенты т увеличиваются с удалением от оси 2, стремясь к единице.
Коэффициенты т, учитывающие точечность источника нагрева, показывают, что в областях, близких к источнику нагрева, температура точек на верхней граничной плоскости, по которой движется дуга, выше, чем в соответствующих точках нижней граничной плоскости. В местах, удаленных от источника нагрева, влияние коэффициента т на изменение температуры по толщине пластины мало сказывается, и значение его стремится к единице. На расстоянии г = 46 температура ограничивающих плоскостей отличается от средней температуры [1] не более, чем на 5%.
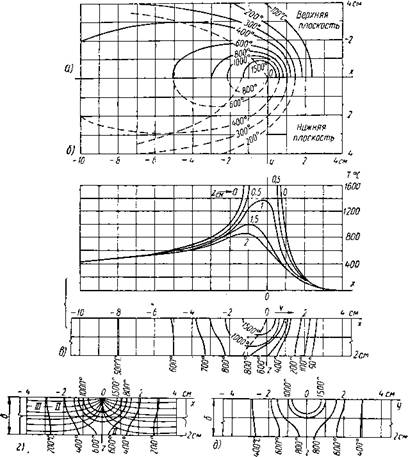
Для более конкретного представления о подвижном температурном поле предельного состояния в толстой пластине на фиг. 7 приведены изотермы распределения температур в пластине толщиной 20 мм. На нагреваемой (верхней) плоскости хоу ■изотермы имеют вид замкнутых кривых, напоминающих подвижное поле в тонких пластинах и на граничной поверхности полубесконечного тела. На нагреваемой (нижней) плоскости пласти-
ны, где 2=6, изотермы напоминают такое же подвижное поле, но с меньшими значениями температур в области, прилегающей к оси 2, и с иной закономерностью распределения температур относительно этой же оси 2. В то время, когда точка с максимальной температурой на нагреваемой плоскости совпадает
|
Фиг. 7. Подвижное температурное поле при нагреве точечным источником пластины толщиной 20 мм: а — изотермы на нагреваемой плоскости z = 0; б — изотермы на нижней плоскости z = S; в — изотермы и кривые распределения температур в продольной плоскости у = 0; г — изотермы и линии теплового потока по поперечной плоскости х = 0; д — кривые максимальных температур в поперечной плоскости * = 0. |
с началом координат, в ненагреваемой плоскости, где 2=6, точка с максимальной температурой будет расположена в 14 мм позади оси 2, проходящей через источник нагрева. Кроме того максимальная температура на ненагреваемой плоскости значительно ниже, чем температура в этой области. на нагреваемой плоскости.
В менее нагретых областях, удаленных от оси z, температура по толщине пластины практически выравнивается. В областях, где температура ниже 200° С, изотермы нагреваемой и ненагреваемой плоскостей почти совпадают (см. фиг. 7).
По продольному сечению xoz пластины (фиг. 7, в) и по поперечному сечению yoz, проходящему через источник нагрева (фиг. 7, г), изотермы показывают неравномерное распределение температуры по толщине пластины в областях, прилегающих к оси г, и выравнивание температуры по толщине пластины в местах, удаленных от оси г.
Геометрическое место точек, имеющих наибольшие температуры при заданном положении подвижного источника нагрева, показано пунктиром на фиг. 7, а, б.