ВНУТРЕННИЕ УСИЛИЯ И ДЕФОРМАЦИИ ПРИ СВАРКЕ
ТЕМПЕРАТУРНОЕ СОСТОЯНИЕ МЕТАЛЛА ПРИ СВАРКЕ Температурное поле при сварке тонких пластин
Температурное поле представляет совокупность мгновенных значений температур во всех точках изучаемого пространства или рассматриваемого тела в данный момент времени. Температурное поле изображается при помощи изотермических линий или изотермических поверхностей.
При сварке изделия сосредоточенным источником тепла производится интенсивный кратковременный местный нагрев металла до высоких температур. Тепло, выделяемое источником нагрева, расплавляет небольшой объем металла в месте сваривания и вследствие теплопроводности распространяется в прилегающие слои основного металла. За короткое время температура металла в месте сварки изменяется в широких пределах: от температуры окружающей среды до температуры плавления; затем по мере удаления источника нагрева металл остывает. При этом в сварочной ванне происходят физико-химические и металлургические процессы, а в наплавленном и основном металле — структурные и объемные изменения. Большая скорость нагрева при сварке и сравнительно быстрое охлаждение создают в сва-риваемом металле неравномерное температурное поле со значительным падением температуры при переходе от места сварки к холодным участкам металла.
Рассмотрим подвижное температурное поле при нагреве сварочной дугой тонкой пластины.
Тонкими пластинами называют такие, в которых при однопроходной сварке распределение температуры по толщине можно считать равномерным, т. е. в рассматриваемой точке пластины температура по толщине металла одинаковая.
В начальный период сварочного нагрева температурное поле будет неустановившимся. Температура отдельных точек свариваемого металла с увеличением времени нагрева будет повышаться до некоторых предельных значений, при которых темпе-
ратурное поле достигнет своего предельного состояния и в дальнейшем остается неизменным, т. е. установившимся.
При нагреве сварочной дугой предельное состояние температурного поля в области, близкой к источнику нагрева, практически наступает довольно скоро после начала сварки. При элек- тродуговой сварке установившееся предельное подвижное температурное поле наступает после нескольких минут, а иногда даже нескольких секунд. Установившееся предельное температурное поле движется вместе С дугой ПОСТОЯННОЙ МОЩНОСТИ ПрЯМОЛИ' 'нейно и равномерно с постоянной скоростью V. Такое поле будет квазистационарным. Изотермы :квазистационарного температурного поля движутся с ним поступательно с той же скоростью, не изменяясь по величине. В подвижном квазистационарном поле температурное состояние металла, наблюдаемое в сечении 1 в момент времени 11, повторяется в параллельном сечении 2 в момент времени t2 и т. д.
Наиболее полное исследование температурного поля при сварке произведено Н. Н. Рыкалиным [1]. Приняв ряд допущений^ Н. Н. Рыкалин теоретически и экспериментально исследовал температурное состояние металла в разных точках поля для случаев, когда источник нагрева при сварке неподвижный и когда он движется прямолинейно и равномерно вдоль шва.
При электродуговой сварке тонких пластин схему распространения тепла от источника нагрева принимают линейной, как показано на фиг. 1 (линия 00'), т. е. считают, что все тепло, воспринимаемое пластиной от источника нагрева, распространяется от линии 00' и вследствие теплопроводности нагревает прилегающие слои металла.
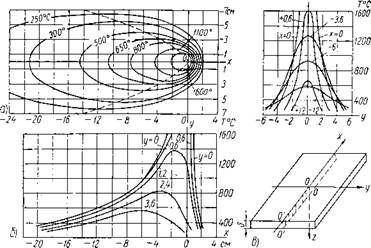
При нагреве пластины по схеме линейного источника температурное поле будет плоским. Температура в каждой точке поля по толщине пластины считается одинаковой.. Температурное состояние точек пластины в плоском поле определяется двумя координатами х и у. Изотермы плоского температурного поля представляют собой замкнутые цилиндрические поверхности, построенные на изотермических «кривых. Образующими этих поверхностей служит толщина пластины. На поверхности пластины изотермы подвижного плоского температурного поля имеют вид вытянутых вдоль линии шва замкнутых кривых, которые перемещаются с постоянной скоростью вместе с источником нагрева, не изменяясь по величине (фиг. 1, а). Центр подвижной системы координат совпадает с положением движущегося источника нагрева.
Наиболее крутое падение температуры образуется впереди источника нагрева там, где изотермы очень сгущены. Крутое падение температуры наблюдается также в направлении оси у. Сварочная дуга как бы сгущает изотермы впереди себя и сбоку. В направлении, обратном движению дуги, изотермы вытянуты, а градиент падения температуры невысокий.
Плоское температурное поле образуется при сварке однопроходным стыковым швом в том случае, когда проплавление основного металла обеспечивается по всей толщине пластины. Практически тепловой расчет по схеме нагрева линейным источником можно применять при автоматической сварке под флюсом для пластин толщиной до 16—20 мм, свариваемых обычно за один
|
Фиг. 1. Подвижное плоское температурное поле в бесконечной тонкой пластине по Рыкалину: а — изотермы подвижного поля; б — кривые распределения температуры по линиям, параллельным оси ох-% в — кривые распределения температуры по линиям, параллельным оси оу. |
проход. Температура в любой точке плоского температурного поля в градусах определяется по формуле Н. Н. Рыкалина:
где г — расстояние точки от источника нагрева, равное Ух2у2 х — координата точки до начала подвижной системы координат;
q — эффективная тепловая мощность источника нагрева в кал/сек (для электрической дуги q = г • 0,24/6/, где / и U — ток и напряжение сварочной дуги); т] — коэффициент использования тепла, принимаемый в пределах: при сварке угольным электродом 0,50—0,70, при сварке открытой дугой металлическим электродом 0,70— 0,80 и при сварке под флюсом 0,75—0,90; v — скорость перемещения источника нагрева по оси х в см/сек;
8 — толщина пластины в см
X — коэффициент теплопроводности в кал/см • сек град; а — коэффициент температуропроводности в см2/сек (а = —, где су — объемная теплоемкост)ь; b — коэффициент температуроотдачи в 1/сек; Ъ =
km — коэффициент поверхностной теплоотдачи радиацией в кал /см2 • сек град]
Ко (Ц)—бесселева функция нулевого порядка второго рода от мнимого аргумента.
В табл. 1 приведены значения функции Ко (^) Для некоторых значений аргумента (и).
|
Таблица 1 Значения функции Ко (и) для некоторых значений аргумента
|
Из уравнения (1) видно, что температура в любой точке пластины возрастает с увеличением интенсивности источника нагрева q и с уменьшением скорости движения дуги v. Значение со-
_ —
множителей е 2а и Ко (^) убывает с удалением точки от источника нагрева, что свидетельствует о большой концентрации тепла около источника нагрева и о резком снижении температуры в удаленных от источника нагрева точках металла.
При нагреве тонких пластин неподвижным источником предельное температурное состояние металла в каждой точке наступит тогда, когда приток тепла к этой точке пластины будет равен потерям его в этой же точке. Изотермы неподвижного плоского температурного поля предельного состояния представляют концентрические окружности, которые сгущаются к центру, где расположен источник нагрева. Температурное поле располагается симметрично относительно источника нагрева, и градиенты падения температуры будут одинаковыми по всем направлениям от - центра. Температуру точек пластины при нагреве ее неподвижным линейным источником до предельного состояния можно определить на основании уравнения (1), которое при v = 0 будет
В неподвижном плоском поле предельного состояния наиболее высокая температура будет у источника нагрева, а с удалением от центра она падает в соответствии с изменением функции Ко{и)~
|
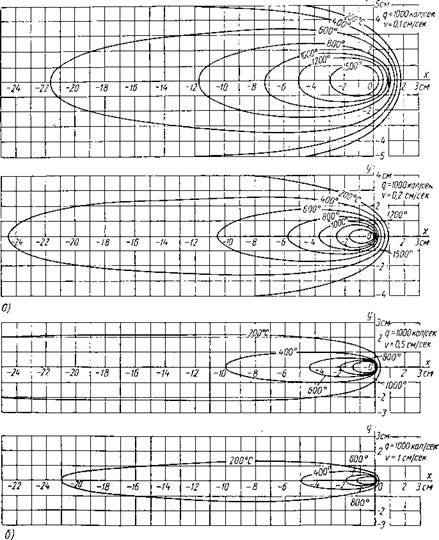
Фиг. 2. Влияние скорости движения дуги на форму подвижного температурного поля в пластине: а — при v = 0,1 см/сек и г>= 0,2 см/сек б — при v ■= 0,5 см [сек и и 1 см /сек. |
В подвижном температурном поле характер изменения температурного состояния точек свариваемого металла зависит от ско -
роста движения источника нагрева. С увеличением скорости сварки изотермы подвижного температурного поля становятся более вытянутыми. Области нагрева металла до высоких температур становятся более узкими. На фиг. 2, а показаны изотермы для случаев сварки электрической дугой одинаковой мощности на различных скоростях.
При большой скорости сварки распределение температур в поперечных сечениях пластины позади источника нагрева примерно одинаковое, так как условия нагрева и теплоотдачи для каждого сечения, кроме крайних, почти тождественны. Изотермы температурного поля становятся вытянутыми в направлении движения дуги. Область нагрева металла до высоких температур сосредоточивается на узкой полоске вдоль оси х. Температура соседних точек, лежащих на одинаковом расстоянии от линии нагрева (точек, лежащих на линии у = const), почти одинакова (фиг. 2,6).
Для каждой точки свариваемых пластин в любой момент времени нагрева мощным быстродвижущимся источником температура может быть определена по формуле Н. Н. Рыкалина
|
|
(3)
где у — расстояние точки от оси шва;
t — время, отсчитываемое с момента прохождения источником тепла линии оу, на которой лежит рассматриваемая точка.
По формуле (3) можем найти распределение температуры в поперечных сечениях, параллельных оси у и лежащих позади движущегося источника тепла.
При сварке под флюсом потери на теплоотдачу в окружающую среду ничтожны и ими можно пренебречь. В этом случае температура в разных точках пластины определяется по формуле
Максимальная температура точек при сварке пластины мощным быстродвижущимся линейным источником определяется по формуле
|
|
где у — расстояние от оси шва в см.
Так как коэффициент темпер ату роотдачи 6=—у, а коэффи-
|
|
|
циент температуропроводности а = —, то после подстановки их значений формула (4) примет вид |
|
I |
Для стали примерное значение коэффициента поверхностной теплоотдачи km = 0,0008, а значение коэффициента тёплопроводно - km 0,0008
сти А = 0,1, поэтому = —д 1 = 0,008. Максимальная темпера
тура нагрева точек при сварке стальных пластин, исходя из формулы (4,а), определяется выражением
W«L(,_0,008£). (46)
Двучлен ^1—0,008-уj учитывает потери энергии на поверхностную теплоотдачу. С уменьшением координаты у и увеличением толщины свариваемых пластин величина двучлена (1 —
и2
— 0,008 стремится к единице, и влияние поверхностной тепло
Тт ах-
отдачи на температуру точек, лежащих вблизи шва, становится мало заметным. Так, в точках, лежащих на расстоянии от оси шва у = 2 см при сварке стальных пластин толщиной 1 см величина 1 — 0,008 • 4 = 1 — 0,032 = 0,968, что отличается от единицы примерно на 3%. При значениях координаты у < 2 см
двучлен ^1—0,008-у j будет отличаться от единицы меньше чем
на 3%, и влияние его на значение температуры по формуле (46) станет ничтожным. В таком случае при определении наибольшей температуры в точках, расположенных близко к шву, можно не учитывать поверхностной теплоотдачи и пользоваться приближенной формулой
Т — 0*484? (4В
Ymax“ 2 vbc^y *
Пространственное температурное поле при сварке
При местном нагреве металла большой толщины температурное поле имеет пространственный характер. Расчет температурного поля производится по схеме нагрева точечным источником. По толщине металла температура распределяется неравномерно. Температура каждой точки металла определяется тремя координатами. Пластину металла большой толщины, с точки зрения нагрева сварочной дугой, можно рассматривать как полубесконечное тело, на граничной поверхности которого находится точечный источник нагрева. Такое допущение основано на том, что в металле большой толщины подвижное температурное поле практически затухает в отдаленной массе металла. Влияние нижней ограничивающей поверхности мало сказывается на распределении температуры в пространственном поле. При электродуговой сварке расчетная схема точечного источника применяется для металла толщиной свыше 50 мм.
10
Местный нагрев полубесконечного тела существенно отличается от нагрева тонких пластин. В то время как при нагреве тонких пластин большую роль играет внешняя поверхностная теплоотдача, в полубесконечном теле последняя весьма незначительна по сравнению с внутренней. В полубесконечном теле почти вся тепловая энергия, создаваемая источником нагрева, воспринимается металлом. В пространственном температурном поле концентрация тепла у источника нагрева значительно сильнее, чем в плоском поле. Предельное температурное состояние температурного поля в полубесконечном теле при подвижном точечном источнике нагрева наступает раньше, чем при нагреве тонких пластин.
Температура в любой точке полубесконечного тела при установившемся (предельном) подвижном пространственном поле без теплоотдачи определяется по уравнению:
vx vR
Т (R, х) = ■ е~Та ~ Та, (5)
где х—координата расстояния точки от подвижного источника нагрева по направлению сварки;
R — расстояние точки до источника нагрева, т. е. радиус-вектор;
v — постоянная скорость перемещения дуги в см/сек; q — эффективная мощность в кал/сек; і — коэффициент теплопроводности металла; а — коэффициент температуропроводности; е — основание натуральных логарифмов.
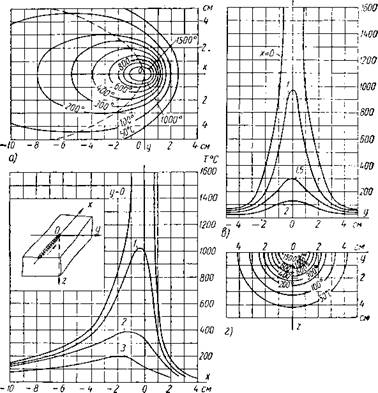
На фиг. 3 изображено подвижное пространственное температурное поле. Изотермические поверхности пространственного температурного поля представляют половины замкнутых поверхностей вращения относительно линии движения источника нагрева оси х. Изотермические поверхности вытянуты в направлении оси х и сгущены впереди источника нагрева (фиг. 3,а).
Температура любой точки, определяемая по формуле (5), зависит не только от расстояния до источника нагрева R, но и от положения этой точки относительно плоскости yoz, т. е. от координаты х. Наибольшие градиенты падения температуры будут впереди источника нагрева в направлении оси х в плоскостях хог. Крутое падение температуры будет также в плоскости yoz, перпендикулярной линии сварки. Наименьшее падение температуры наблюдается позади источника нагрева в плоскости xoz при отрицательном значении координаты х.
На основании формулы (5) температура точек на координатной плоскости yoz, где х = 0 (фиг. 3, г) определяется выражением
Температура точек на координатной плоскости xoz, где у = О (фиг. 3, б) впереди источника нагрева при х > 0 в точке х = R определяется выражением
_vR
Т (х = R) —
|
2лА R Т°с
6) Фиг. 3. Подвижное пространственное температурное поле в полу - бесконечном теле по Рыкалину: а — изотермы по граничной плоскости хоу б — кривые распределения температуры в плоскостях, перпендикулярных к оси оу в — кривые распределения температуры в плоскостях, перпендикулярных к оси ох; г — изотермы в плоскости yoz. |
Предельная температура точек на координатной оси х позади источника нагрева, где х < 0 определяется выражением
T(x = ~R) = 2^Ьг' <8>
Наибольшая область нагрева и наименьшие градиенты падения температуры будут позади движущегося источника тепла* 12
В этой области температура точек на координатной оси х не зависит от скорости перемещения дуги и определяется только расстоянием R этих точек от источника нагрева по формуле (8).
С увеличением скорости движения мощного точечного источника нагрева изотермические поверхности в полубесконечном теле становятся более вытянутыми в направлении линии нагрева. Около оси х располагаются области металла, нагретого до наиболее высоких температур.
Температура точек полубесконечного тела, лежащих на небольших расстояниях г от линии перемещения (от оси х) быстродви - жущегося точечного источника нагрева приближенно определяется по формуле
где г = VУг + г2 — расстояние точки от оси х, а у и г— координаты этой точки; t — время, отсчитываемое от момента прохождения источником теплоты плоскости у'о'г', в которой лежит рассматриваемая точка. Максимальная температура точек, лежащих в плоскости yoz и несколько удаленных от оси ху наступает через некоторое время после прохождения источником нагрева плоскости yoz. Практический интерес представляет определение максимальной температуры точки полубесконечного тела. По исследованиям Н. Н. Ры - калина максимальная температура в точках полубесконечного тела при предельном состоянии нагрева быстродвижущимся точечным источником прямо пропорциональна погонной энергии
источника и обратно пропорциональна квадрату расстояния
этой точки от оси х. Максимальная температура точки в полубесконечном теле определяется по формуле
'т1 __ 0,736д /дч
шах пис^іг2* '
где q — эффективная мощность дуги в кал/сек; v — скорость движения дуги в см qf — объемная теплоемкость металла; г — расстояние точки от оси шва (г = У у2 + z2).
При нагреве полубесконечного тела неподвижным источником изотермы представляют собой сферические поверхности, центр которых совпадает с источником нагрева. Температура точек полубесконечного тела при предельном состоянии нагрева неподвижным источником определяется по уравнению (5) при условии v = 0
Т = ЪilR ’
где R — расстояние точки до источника нагрева, т. е. радиус сферы.
Предельная температура точек полубесконечного тела при нагреве неподвижным точечным источником изменяется обратно пропорционально радиусу R и находится в прямой зависимости от эффективной мощности источника нагрева. С приближением точек к источнику нагрева температура их резко повышается, так как
при малых значениях R отношение возрастает, поэтому концентрация тепла у источника нагрева весьма значительная.
Изотермы температурного поля предельного состояния при нагреве полубесконечного тела неподвижным точечным источником представляют собой концентрические полусферы. Градиент падения температуры в полубесконечном теле во всех направлениях от неподвижного точечного источника одинаковый. Область высоких температур концентрируется около источника нагрева, а в отдаленных слоях температура снижается равномерно.