ТЕПЛОПЕРЕДАЧА В СТРОИТЕЛЬСТВЕ

Коэфицненты

9. Коэфициент теплопроводности материала огра­ждений X весьма различен для различных строительных мате­риалов. Он зависит от их состава, плотности, физического строе­ния и ряда других свойств, еще не вполне исследованных. Но и для одного и того же материала с определенной плотностью он не является постоянным: он сильно зависит от степени влажности дан­ного материала и в меньшей степени — от его температуры. Поэтому при определении таких коэфициентов экспериментальным путем в совре­менных исследованиях учитываются эти факторы и проставляются в таблицах полученных выводов. В табл. I приложений помещены эти данные для разных строительных материалов в воздушно-сухом состоя­нии, при этом для более точной характеристики материалов, к которым относятся табличные коэфицненты, указан еще их вес 1 м[3].

С ростом температуры коэфицненты X всех строительных материалов повышаются, хотя и очень незначительно[4]. Поскольку многие строи­тельные материалы, особенно же рыхлые и искусственно пористые,
имеют в практике весьма колеблющуюся степень плотности (веса 1 мя), в таблице приводятся для них коэфициенты X в зависимости также 41 от этого фактора.

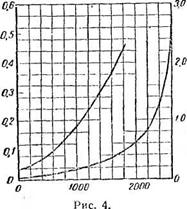
Зависимость коэфициента X разных материалов от объемного веса может быть изображена для всех неорганических материалов в совер­шенно сухом состоянии кривой, предложенной Каымерером (Cammerer); она представлена на рис. 4 в двух масштабах (вертикальных отложений), так что левая кривая представляет лишь детализацию части правой. Из диаграммы виню, насколько непра­вильно было бы принимать прямую пропорциональность между объемным весом и коэфициенгом X разных строительных материалов. Такая зави­симость не только не оправдывается фактами, но неправильна и принци­пиально: различие объемных весов у разных материалов (при едином весе абсолютно плотного вещества их) от­ражает лишь различие в общем коли­честве возтушных пустот в них, но не способ распределения этих пустот по всему объему, т. е. структуру их. Д эта последняя является бесспорно немаловажным и самостоятельным фактором. Простой эле­ментарный расчет показывает, что чем равномернее распределены пустоты и следовательно чем они мельче (при толі же общем их объеме в теле), тем меньший коэфициеит будет получаться у материала.

10. Влияние на коэфициеит X влажности материалов[5] гораздо более существенно. Данные этого рода для некоторых (более исследо­ванных в этом отношении) строительных материалов помещены в таблицах, причем надо заметить, что материалы строительных огра­ждений, разделяющих зоны разных температур, никогда не бывают не только совершенно сухими, но даже к воздушно-сухими в точном смысле слова, так как помимо естественной гигроскопичности в отно­шении наружной и внутренней атмосферы конденсируют в себе еще часть постоянно проходящих через них паров. Процесс этот исследо­ван ближе н главе 3 части I.

Позднейшие исследования в области влияния влажности! материалов на коэфициеит их внутренней теплопроводности принадлежат Д-ру инж. Каммереру. Особенно интересны его новые данные о пористых материалах в смысле более точного определения понятия их „нормаль­ной влажности" и связанных с этим практических коэфициентов. Эти последние исследования произведены им в 1929 и 1930 гг. на весьма многочисленных объектах реального поселкового строительства Гер­мании и доложены XIII Конгрессу по отоплению и вентиляции 1930 г. К Приведем вкратце основные результаты этих исследований.

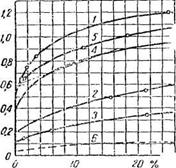
На рис. 5 приведены кривые Каммерера для повышения коэфи - циента X у материалов вместе с ростом их влажности по объему.

Под № 1—С фигурируют кривые сле­дующих материалов:

Обьеі. ныв

V6 Материал пес в кг

1 TOC o "1-5" h z Кирпичная кладка ■ • • . 1№0

2 Плиты пемзового бетона. 1 150

3 Высокопористые кирпичи 727 -1 Известковый раствор • . . 1 650

5 Кирпичная кладка.... 2000

6 Пробковые кирпичи. - . 200

Из тех же исследований можно I ^обгема вьшести следующую зависимость коэф­фициента X от влажности для всех вышеперечисленных м а т е р и а - < лов одинаково2:

При таких условиях приобретает большую важность для практики вопрос о том, какой же процент влажности считать нормальным для разных строительных материалов, чтобы е соответствии с этим пра­вильно выбирать их коэфицненты. По тем же исследованиям Камме­рера за нормальный процент влажности по объему следует принимать для разных материалов при возведении из них наружных стен:

TOC o "1-5" h z Кирпичная кладка.................................... 0,2—1,0 в среднем 0,5

Бетон, гипс 4—10 7

Теплый бетой........................................... • 5—17 „ „ 13

Глина - 4—70 „ „ 7

Такое различие объясняется повышенной сорбцией влаги и водя­ных паров высокопористыми материалами в силу особенностей их струк­туры (формы пор и пр.).

Для стен пустотелых, если в них устранена опасность конденса­ции паров, а также для всех внутренних стен нормальная влажность составляет:

при обыкновенной кирпичной гладке „ высоьопорпстых материалах. - .

Наконец совершенно cvxoe состояние материала и связанный с ним коэфициеит X принимаются только для изоляционных плит, тщательно загудронированных и расположенных в условиях, исключающих какое - либо отсырение в самой конструкции.

Подробная таблица, разработанная Каымерером на этих основаниях, приведена в приложении II, где приведены также и эквиваленты для разных стенок из разных материалов, выраженные в единице, равной нормальной немецкой стеке 38 см; для наших русских условий эта единица лолжна быть принята в 1,5 раза больше (следовательно соот­ветствующие цифры таблицы должны быть во столько же раз умень­шены).

Наконец тем же исследователем дана [6] таблица изменений коэфн - цнента X твердого материала при его полном насыщении влагой срав­нительно с коэфициентом его при абсолютно сухом состоянии. За ис­ходное состояние автор берет при этом идеальный твердый материал, совершенно непористый, с коэфициентом Х=2,8 (при температуре 20°). Тогда в зависимости от других степеней пористости коэфициенты X при сухом и насыщенном состоянии будут следующими:

В приложении даны практические коэфициенты X Каммерера для строительных материалов [7]

11. Коэфициенты а теплообмена между поверхно­стями стены и прилегающим воздухом зависят по своей величине главным обраозм от влияний двух порядков:

1) Непосредственного соприкосновения поверхности степы с воз­духом.

В силу зтого теплота передается частью кондукцией, т. е. путем внутренней теплопроводности прилегающего воздушного слоя в напра­влении, перпендикулярном к поверхности стены, частью же путем п е - реноса теплоты движением воздуха вдоль стены, — конвек­цией, каковая зависит, естественно, от скорости указанного движе­ния. Влияние обоих этих процессов на тепловую потерю пропорци­онально площади стенной поверхности и разности температур ее и воздуха; обозначив коэфициент этой пропорциональности через а. (а „конвекции"), имеем для частной теплопередачи этим путем:

yi = oB-F(/ —Г). (9)

2) Теплового лучеиспускания поверхности стены.

Рассматриваем его пока совершенно независимо от взаимоотноше­ния с температурами окружающих других предметов и даже вообще от наличия последних. В таком случае это лучеиспускание зависит от абсолютной температуры поверхности, т. е. величины t-- 273°, а именно, по закону физики (Стефана и Больцмана) оно пропорционально четвер­той степени ее; кроме того оно конечно пропорционально площади лучеиспускающей поверхности. Таким образом количество передавае­мой в этом процессе теплоты может быть выражено формулой:

Q = з • F(*-f 273)4,

где з есть коэфициент пропорциональности, характеризующий способ­ность лучеиспускания данной материальной поверхности. Обозначив i-j-273 через 0 и произведя для упрощения формулы некоторые арифметические изменения, получим:

где С (равное о - Ю8) есгь характеристический коэфициент физики для излучения данного тела, — коэфициент излучения.

В приложении III даны коэфицненты лучеиспускания С для разных строительных материалов и при разных видах отделки их поверхно­стей.

Но этому потоку лучеиспускания от стены противостоит подобный же поток лучеиспускания на нее со стороны прилегающей среды (дру­гих ограждений и предметов); этот поток может быть менее или более первого п зависимости от соотношения температур н других условий, и таким образом окончательный тепловой результат этого взаимодей­ствия получится лишь при совместном учете обоих процессов. Способ этого учета дается физикой в виде формулы:

где 0, и 02 суть абсолютные температуры стены и среды (окружаю­щих предметов), а С' есть так называемый приведенный коэфициент излучения двух противостоящих друг другу материалов, выбираемый r зависимости от коэфициентов лучеиспускания С, и С, г каждого из двух материалов и коэфициента С абсолютно черного тела по табл. IV приложения. Присоединяя к этим выводам добавления О. Кноблауха и К. Хенки, имеем формулу:

Q2 = С'с ■ F - (tx — 4), (10)

где tx—температура стенной поверхности, /2—температура окружаю­щей среды (противостоящих предметов и воздуха) и с — коэфициеит, учитывающий влияние четвертых степеней абсолютных температур лучеиспускающих друг на друга материалов. Величины этого коэфици­ента приведены в приложении V 4

Сложив уравнения (9) и (10), получим выражение для общей тепло­передачи между стенной поверхностью и воздухом:

Q3 = Q, - f Q2 = («к+С'С) F (tx—4).

Сопоставляя это с уравнением (2), заключаем, что коэфициенты а для теплообмена между стеной и воздухом, входящие в уравнение (2) и в уравнение (4), имеют следующее общее для них выражение:

а = аг -(- С'с.

Более конкретное определение этой величины с выводом отдельных значений для теплопередачи от внутреннего воздуха к стене [т. е. коэфициента ав в формуле (4)] и от стены к наружному воздуху [коэ - фипиента ан в формуле (4)] представило большие трудности для ис­следователей ввиду сложных влияний абсолютных 'температур (коэфи - циент с) и скорости движения воздуха (коэфициеит ак) . Для нужд строительной практики при небольших сравнительно температурах ма­териалов и небольших скоростях движения воздуха оказалось возмож­ным упростить рассмотрение. Именно, были приняты лишь некоторые типовые значения для с. Что же касается ау, то эта величина была исследована Нуссельтом и рядом других ученых для двух основных случаев практики: при естественной конвекции воздуха около стены и при повышенной его подвижности от внешней силы -.

12. Естественная конвекция воздуха около стены происходит ис­ключительно от разности температур воздуха и стены и в силу огра­ниченной величины этой разности в обычных условиях строительной практики дает вообще небольшие скорости воздушного потока по по­верхности стены. Тем не менее коэфициеит схг зависит, во-первых, от указанной скорости и следовательно от разности температур. Затем он зависит от направления конвекции, т. е. от того, вертикальная или го­ризонтальная поверхность ограждения соприкасается с воздухом; при этом для горизонтальной поверхности конвекция имеет место лики.

1 Подробнее об излучении см. часть IV, главу 2.

■ 2 Мы не касаемся здесь ряда теоретических и экспериментальных работ общенаучного значения: Шмидта и Бекмана, Пуссельта, Мчссенара и др., ограни­чиваясь лишь удобнейшими для практики выводами.

в том случае, если тепловой ноток идет от нее снизу вверх (поверх­ность потолка на чердаке), так что согревшийся около нее воздух под­нимается вверх и сменяется более холодным; если же тепловой поток идет сверху вниз (например, от нижней поверхности пола в подполье), то конвекция не имеет места, так как согревшийся около поверхности воздух как более легкий остается без движения около нее.

Наконец имеет некоторое значение и то, является ли прилегаю­щий воздух внутренним или наружным (даже при абсолютном безвет­рии) Таким образом были найдены следующие выражения для о.:

1) Вертикальные стены:

а) наружные при разности температур Д/<[ 5°:

ак = 3+0,08^ и при разности Дt > 5°:

«к = 2,2 Ї/Af,

б) внутренние стены между помещениями с разной температурой при всех разностях Дt:

aK = 2’2V~&>

2) Горизонтальные ограждения помещений при направлении тепло­вого потока снизу вверх:

а,: = 2,8

3) Горизонтальные ограждения помещений при направлении тепло­вого потока сверху вниз:

а — 0.

1C

Эта последняя величина принимается, очевидно, как некоторая ус­ловность вместо очень малых, но неизвестных величин, происходящих от упомянутой выше непосредственной теплопроводности от стены в ближайший слой воздуха в перпендикулярном (к стене) направлении, каковой процесс имеет место и при отсутствии конвекции.

Прибавляя ко всем чтим выражениям для а величину (Ус, полу­чим полные значения для коэфициентов а теплообмена между стеной и воздухом при условии отсутствия всякого движения последнего по­мимо вызванного разностью температур его и стенной поверхности. Величины 'j. f можно брать также из таблицы (приложе ше VI"), соста­вленной по приведенным формулам Нуссельта.

Выше мы привели результаты обследований в том виде, как они были обработаны у К. Хенки. В последующие годы новые исследова­ния были предприняты Внрцем, который дал несколько иную формули­ровку расчету коэфициентов а н я. Остановимся здесь только на окончательных выводах.

По Вирцу для передачи теплоты от воздуха к стене п р и Дt ;> 5е:

а = 0,55 Ш0'23,

следовательно:

« = С'с-}-0,55/ДЛ2

где I есть коэфициент, лежащий между 3 и 6 (а именно при у, д°

/=4 для воздуха в помещении, 1=5 для неспокойного внутреннего

воздуха или спокойного наружного, I = 6 для наружного в о«бцчном движении); С'—приведенный коэфициент лучеиспускания по Таблице (приложение IV).

При Дt ■< 5° остается и для внутренней поверхности степи упомя­нутое выше уравнение Нуссельта, по которому ав = (Ус rj — = С’с -4- З -4- 0,08 At. В приложении VI приведены значения « по

1 * К

формуле Вирца.

Для передачи теплоты от стены к воздуху Вирц оста­новился на уравнении:

а — С'с 13 V гі,

II I [8]

где v — скорость движения окружающего воздуха (естественная или

искусственно повышенная).

Приведенные данные значительно облегчают расчеты этого рода. Однако в практических расчетах нам обычно, не бывает заранее извест­ной указанная разность температур Дt: строителю задаются «Золыней частью лишь температуры внутреннего и наружного воздуха Т и у. В таком случае можно применять следующий весьма точны!! прием расчета коэфициеитов а. Из уравнения (2) имеем:

7r=“(*„ — TJ = a-At,

а из уравнения (3):

T = b(TB~TJ.

Приравнивая правые части уравнений, получим:

Д t k

~ а "

Определяем далее к из уравнения (4); поскольку мы пока не раз­личаем в этом последнем уравнении ап и ав, можем определить из него к следующим образом:

1 =1-1-1 к а ^ X ’

где y еегь величина термического сопротивления стенного слоя

Таким образом имеем:

At

в ’ 2 + а:-^

— коэфициеит теплопроводности стены^. Эго уравнение и мо­жет служить для проверки пробных подборов величин Дt и со­ответствующих им по формулам для ак или по приложению VI вели­чин а. Для облегчения таких подборов служит следующая таблица

Af

ДЛЯ величин... у.- .

1 В * и

С' =

— = 1,0

е

1,5

2,0

5,0

Приведем пример. Требуется определить а. для наружной стены с® следующими заданиями: —=1,5, С' — 4, Т — -(- 20°, 7 = 0°. По при-

Ы

веденной таолице для данного случая можно взять •=------------------ =- предноло-

в в

жительно равным ; так как Гв—7^ = 20°, то At надо предпола­гать — - у • 20 -- 3,1°. Тогда из приложения VI имеем: ав = 3,25, сле­довательно а = 4 -)- 3,25 = 7,25. Вставляя эту величину в правую часть проверочного уравнения, имеем:

д/ 1 1 20

■, или дг = £-=-= .5,94.

1„— 7„ 2 - f - 7,25: 1,5 6,82 ’ 6,82'

Таким образом из проверочного уравнения получилась величина для At меньшая, чем мы предположили первоначально для этой раз­ности (3,1°) при а = 7,25; теперь возьмем для а немного меньшую ве­личину, а именно 7,23, и, вставив в то же проверочное уравнение,, убедимся, что последнее дает нам Д£ = 3,1°.

Такой расчет бывает нужен лишь в случае требований большой точности. В обычных практических расчетах довотьствуюгся некото­рыми стандартными величинами коэфициентов а (см. ниже).

13. До сих пор мы рассматривали главным образом коэфициенты а,, получающиеся при естественной конвекции воздуха около стены. Если скорость движения воздуха увеличена посторонними внешними - силами, например силами ветра около наружной поверхности стены.

или влиянием большой искусственной вентиляции внутри помещения, то величины коэфицнента а возрастают. Так, по Реккнагелю имеем:

При скорости воздуха в м/сек................................. О 1 4,5 5,5

Коэфициент.......................................................... о = б 23 30 36

По Нуссельту при скорости воздуха в 3 м/сек а. к = 25, следовательнс ая=;29.

По позднейшим исследованиям Вирна и его формуле, приведенной выше, имеем при с = 0,85 (средняя величина для разных температур):-

При v = м/сек 0,3 0.4 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5.5 0,0

ап = 11 12 13 17 20 22 24 26 28 30 31 33 34 36

В расчетах строительной практики эти последние коэфицненты при­меняются обычно для внешней поверхности наружных ограждений:,

при этом принимают:

а) для стен зданий, расположенных в открытых местах,

подверженных ветрам, или выше окружающих зданий. . а = 25;

б) для стен зданий, расположенных в городе среди

общей застройки... •.............................. •...................... «н = 20;

в) для стен зданий, не подверженных действию вет­ров (например стоящих в лесу или среди более высо­ких зданий)................................................................................................................. се...... = 15 [9];

г) для горизонтальных поверхностей, обращенных к закрытым холодным помещениям при теплопередаче снизу

вверх (поверхность потолка на чердаке)............................................. а.... =10—12*

д) для горизонтальных поверхностей, обращенных к закрытым холодным помещениям при теплопередаче сверху

вниз (поверхность пола в подполье) -.................................................. а..... = 5.

Напротив, коэфициент ав в формуле (4) обычно исчисляется по приемам, формулам и таблицам, относящимся к естественной конвек­ции (см. приложение VI). В практике расчета отоплений он берется:

а) для вертикальных стен с нормальной теплопровод­ностью или близкой к ней (следовательно с обычной раз­ностью температур внутренней поверхности стены и воз­духа) = 7— 7,5,’

б) для горизонтальных перекрытий (потолков) при теплопередаче снизу вверх. . . • а = 7.5;

ву то же при теплопередаче сверху......... вниз (полы ниж­него этажа) . • - • = 7;

г) при искусственно повышенных скоростях — по формуле Вирца. В 1931 г. Каммерер в сотрудничестве с Diirliammer опубликовал я „ Archiv f. Warmewirtschaft“ № 6 следующие величины коэфициента ав в жилых зданиях по своим измерениям в натуре:

Эти величины сильно расходятся со всеми, выдвигавшимися ранее. Ввиду некоторых сомнений в правильности этих измерений (в части излучения) было бы преждевременно придавать им практическое зна­чение.

Влияние воздушных прослойков

14. Обычные расчеты теплопотерь ограждениями предполагают, что за исключением поверхностей эти ограждения передают теплоту во всех своих слоях только кондукцией, при каковом условии тепло­проводность каждого слоя имеет выражение = Иначе обстоит дело

в том случае, если среди слоев ограждения находится один или несколько воздушных прослойков, как это нередко делается в строительной практике. При этом строитель исходит из тех сообра­жений, что воздух является одним из наименее теплопроводных матери­алов, особенно в малоподвижном или неподвижном состоянии; в этом последнем он превосходит по своей слабой теплопроводности почти все известные нам строительные материалы. Так как одновре­менно этот материал является крайне легким н совершенно бесплат­ным, то вполне понятно стремление строителей использовать его в качестве термоизоляционного слоя в конструкции ограждений. Но вышеуказанное достоинство воздуха имеет место только в меру дости­гаемой строителем малой величины тепловых лучеиспусканий между стенками пустоты и малой подвижности его в прослойках, учег которой крайне труден. Воздух теплопрозрачен (передает лучеиспуска­ние) и подвижен, эго и отличает принципиально теплопроводность воздушных прослойков от всех других. Поэтому данные эксперимен­тального характера и результаты исследований в этой области пред­ставляют большое значение для теплового расчета этих прослойков,

Теплопередача через воздушный прослоек, подобно сказанному выше о теплообмене между поверхностью стены и воздухом, может быть разложена на три элементарных процесса.

1) Проведение теплоты через воздух в порядке кондукции, как че. тез обыкновенный материал, который представляет определенное сопротивление „поперечному11 тепловому потоку самым фактом заполнения собой прослойка, независимо от того, нахо­дится ли эгот материал в покое или в движении; что привносится добавочно этим последним—мы будем учитывать особо, этот же минимум рассчитываем отдельно как подчиненный особому закону. Коэфициеит этой теплопроводности X - 0,02; обозначив ширину

(толщину) прослойка через ет, можем написать формулу для данного частного вида теплопередачи следующим образом:

пз

где F есть площадь прослойка, перпендикулярная к тепловому потоку, it. и 4 — температуры ограждений, обращенных в прослоек; — = 3bj

eia

есть, очевидно, теплопроводность неподвижного воздушного прослойка и может быть легко вычислена при ).ю = 0,02 и при заданной велн-

Ч1,не сиз в метрах.

2) Проведение теплоты путем конвекции воздуха в прослойке, т. е. путем его движения по обеим ограничивающим поверхностям прослойка (вверх—по более теплой поверхности и вниз — по более холодной). О сущности этого явления мы уже упоминали выше, Здесь, в применении к прослойкам, необходимо отметить, что скорость движения воздуха в прослойке, а следовательно и влияние этого движе­ния на теплопроводность прослойка зависят от целого ряда обстоя­тельств. Для большей ясности здесь надо различать два основных случая:

а) Случай вертикального прослойка. Скорость движе­ния в нем воздуха и его теплопроводный эффект зависят в этом случае главным образом от ширимы прослойка, от его высоты и от разности температур на ограничивающих прослоек материальных поверхностях. Эта последняя разность температур является основной причиной движе­ния воздуха вверх по одной поверхности и вниз по другой; имею­щаяся при этом скорость движения успевает однако развиваться лишь в меру высоты прослойка, после чего происходит удар н поворот потока, т. е. уменьшение его скорости. И наконец, поскольку эти движения одновременно по двум стенкам являются встречными, ширина прослойка обусловливает большую или меньшую степень взаимного трения и сопротивления двух потоков, а с другой стороны, увеличе­ние ее сверх известной меры оставляет в середине прослойка все большее количество воздуха, почти не участвующего в конвекции. Таким образом становится понятным, что теплопроводность прослойка в порядке конвекции увеличивается с увеличением указанной разности температур и высоты прослойка, а с увеличением его ширины умень­шается, но вскоре это уменьшение затухает.

Однако до сих пор еще далеко не достигнуто точного учета всех этих влияний; имеются лишь частичные данные некоторых исследова­телей и только об одном факторе-—ширине прослойков, так как высота их бралась обычно около 0,6— 1,0 м (по условиям аппаратуры). Так, по данным Нуссельта теплопроводность прослойка путем конвек­ции может быть выражена формулой:

t вз

где tx и t„—температуры ограничивающих плоскостей, ет — ширина прослойка в метрах и >.к — некоторый условный коэфициент теплопро-

j '
водности, подбираемый в соответствии с шириной прослойка по следующей таблице:

При евз = см 0 1 2 3 4 5 6 7 8 10 15

= о 0,01 0,02 0,031 0,038 0,014 0,047 0,05 0,051 0,053 0,06

В полученной формуле величина — =8К означает теплопро-

^ва

водность в калориях всего воздушного прослойка от конвекции и получится для приведенных величин евз путем деления на них (по выраженных в метрах) второй графы; мы получим таким образом: При свя = м о 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,10 0,15

си - = t'l = ккпа 0 1,0 1,0 1,0 0,95 0,88 0,78 0,71 0,64 0,53 0,4

б) Случай горизонтального прослойка. Здесь в свою очередь надо различать два случая: этот прослоек может иметь свою более теплую ограничивающую поверхность в качестве верхней гра­ницы или же в качестве нижней. В первом случае не будет никакой конвекции, потому что воздух, нагреваясь около верхней границы, будет оставаться около нее в’ силу уменьшения плотности, не уступая место другим частицам; аналогичное надо сказать и о слое воздуха около нижней границы; здесь следовательно лк = 0. Во втором случае будет происходить процесс непрерывной смены частиц воздуха как около теплой поверхности, так и холодной, т. е. будет иметь место конвекция (перпендикулярно к поверхности и при очень небольшой высоте, а следовательно при небольших скоростях); за отсутствием специальных исследований по этому вопросу в практике принимают, что эффект этой конвекции одинаков со случаем вертикального про­слойка.

3) Проведение теплоты воздушным прослойком путем лучеиспу­скания стенок прослойка одной на другую. Явление передачи тепла лучеиспусканием уже рассматривалось нами выше. Отличие данного случая состоит только в том, что здесь две лучеиспускающне стенки с различными температурами стоят близко одна от другой и могут непосредственно оказывать влияние в зависимости от физических свойств своих материалов и поверхностей.

Таким образом для данного случая имеем формулу:

Qs — C'cF ((j — /2).

Если теперь соединим три рассмотренных элементарных процесса теплопередачи через прослоек в одно целое, то получим для всей теплопередачи прослойка следующую формулу:

Q = + Q, + Q:1 = (§в8 Cc)F(tl~ Q, (9)

или, обозначив сводный коэфициеит, стоящий в первых скобках*

у/

через новый условный коэфициеит —, получим:

^вз

Q= Г nti—tj,

вз

дого строи гелыюго материала с коэфициеитом внутренней теплопро­водности X = 0,12 при таких же изменяющихся величинах его толщины.

Как было упомянуто выше, влияние высоты прослойка и темпе­ратур ограничивающих его поверхностей (следовательно и его собст­венной средней температуры) выяснено гораздо менее. В то время как ширина прослойка оказывает влияние на все три составные части

)/

общего коэфициента теплопроводности прослойка — (а в явной форме

евз

по крайней мере на две из них), высота и температура оказывают влияние более ограниченное, а именно высота — на конвекцию, а средняя температура — на лучеиспускание. Поэтому значение того и другого факторов находится в зависимости от относительной роли соответствующего элементарного процесса теплопередачи в общей теплопередаче. Чтобы иметь в этом отношении основные ориенти­ровочные данные, ниже приводим таблицу процентного участия каждого из рассмотренных выше элементарных процессов теплопередачи в об­щей ее величине при разных значениях величины С'с и е:

Руководствуясь этой таблицей, можем например заранее предвидеть, что уменьшение высоты прослойков, т. е. разделение их на части горизонтальными, параллельными тепловому потоку диафрагмами (про­кладками), оказывая непосредственное влияние лишь на конвекцию, будет иметь мало значения в общей теплопроводности прослойка, так как вся вообще конвекция играет в нем незначительную роль (8—18°/0). Кроме того незначительное уменьшение теплопроводности при этом может быть возмещено, если не провзойдено, увеличением ее от тех сквозных прокладок, которыми достигается это уменьшение высоты.

15. Как выше было упомянуто, бывшими до сих пор эксперимен­тальными исследованиями определена теплопроводность воздушных прослойков только при высоте их 0,6—1,0 .1/. Насколько можно распространять полученные данные на более высокие прослойки? По своему относительному значению вся конвекция в целом имела бы заметіте влияние лишь при малых величинах С'с, т. е. при малых С'" и при малых с; последнее имеет место в холодных прослойках (где с спускается до 0,7), первое же редко бывает ниже 4,0 для обычных строи­тельных материалов. Поэтому с этой стороны пет вероятия ожидать большого изменения найденных свойств прослойков от увеличения их высоты. И другие соображения говорят за то же. Правда, с увеличе­нием высоты возрастает скорость движения воздуха в прослойке; но в узких прослойках это возрастание не может быть большим как по условиям трения двух встречных потоков воздуха так и в силу незначи­тельной разности температур в таких прослойках между обеими стенками; в широких же прослойках увеличение скорости воздуха и самой конвекции не играет большой роли потому, что при увеличен­ной разности температур здесь получает наибольшее значение луче­испускание, а конвекция вообще не оказывает большого влияния на общую теплопроводность (см. таблицу процентов). По всем этим соображениям нет данных опасаться, что полученные до сих пор нормы теплопроводности воздушных прослойков сильно изменятся, когда будут исследованы прослойки больших высот[10].

Подобным же образом можем отдать себе отчет и в значении температур стенок прослойка или его собственной температуры (средней из двух предыдущих). В приложении V видим, как зависит от этой средней температуры величина с. С понижением средней темпе­ратуры величина с уменьшается, поэтому уменьшается С'с (а особенно при высоком С'), а вместе с ним уменьшается общая роль лучеиспуска­ния в теплопроводности прослойка — прежде всего относительная роль (что видно из таблицы процентов в тексте); но так как при этом не возрастает абсолютное значение и остальных двух элементов теплопроводности (для этого нет причин), то заключаем, что вся она уменьшается при этом понижении температуры (и тем значительнее, чем больше С'). Отсюда легко вывести практическое заключение: воздушные прослойки термоизоляционного назначения в строительных конструкциях выгоднее делать в более холодных зонах этих конструк­ций, так как теплопроводность воздушных прослойков при этом уменьшается (как отчасти и у других тел). В части II этой книги при рассмотрении полезной теплоемкости ограждений будет ясен еще новый мотив к такому же расположению воздушных пустот, по крайней мере узких (оно увеличивает полезную теплоемкость ограждения). Наконец в практике за такое же расположение говорит и соображение о том, что при смачивании наружной поверхности ограждения атмо­сферной влагой (дождями, мокрым снегом) расположенная вблизи этой поверхности возтушная пустота ставит тесный предел распростране­нию сырости в глубину ограждения, что сохраняет его термосонроти - вление от снижения сыростью.

Таким образом влияние высоты прослойка и его температуры при отсутствии более точных данных экспериментального характера может быть учтено строителем главным образом с качественной стороны, в количественном же отношении здесь могут быть учтены лишь неко­торые предельные границы этого влияния (благодаря таблице про­центов).

16. Помощью той же таблицы и пробных подсчетов выясняются л другие вопросы о влиянии на теплопроводность пустот тех или иных технических приемов при их устройстве. Перечислим некоторые лз таких вопросов.

1) Значение коэффициента теплоизлучения С стенок прослойка. Как уже было упомянуто выше, главный вид теплопередачи в воздуш­ных прослойках — теплоизлучение (радиация). Поэтому, если составим ограждение из узких воздушных прослойков, а в качестве мембран возьмем листы материала, очень слабо излучающего теплоту, получим конструкцию, весьма эффективную в отношения теплопередачи. Таким листовым материалом является в современной гехн нее „альфоль“ или, что то же самое, „термофоль“—листы алюминия, зажатые в сетке гонких деревянных рамок, скрепленных в одно целое. Таким способом Задается получать легкую стенку толщиною в 5—6 см с жилищным коэфициентом /г = 0,9 и ниже. Эги конструкции ограждений имеют применение главным образом в холодильном транспорте.

2) Значение разбивки воздушного прослойка на ряд более узких материальными диафрагмами, перпендикулярными тепловоыу потоку. Такая разбивка влияет, очевидно, на два элементарных процесса з общей теплопередаче прослойка: она уменьшает конвекцию (с умень­шением свободной ширины в каждом делении) и уменьшает теплопро­водность лучеиспусканием. Последняя по исследованию К. Хенки уменьшается примерно во столько раз, на сколько равных частей разделили мы прослоек[11]. Но конвекция уменьшается в общем менее сильно, третий же элемент — теплопроводность воздуха как не­подвижного материала — не изменяется вовсе, если игнорировать толщину разделительных диафрагм. Отсюда становится понятным, что указанное деление прослойка понижает его общую теплопроводность; темп этого понижения всегда ниже, чем темп деления прослойка, конкретные же величины понижения зависят от относительной роли трех элементарных пооцессов и могут в каждом заданном случае быть - взвешены на основании таблицы процентов. Но так как обычно доля

участия лучеиспускания ппляется доминирующей—и именно при - широких пустотах (доступных подразделению),—то обычное пониже­ние общей теплопроводности бывает довольно велико (например при разделении прослойка на 3 части понижение бывает до 2‘/з раз); более точные данные могут бьпь получены в каждом отдельном •случае путем вычислений но приведенным выше формулам и таблицам. Если учитывать толщину диафрагм, имеющих вообще гораздо большие коэфициенты а, чем неподвижный воздух, то придем к выводу, что для всякой заданной комбинации прослойка н состава диафрагм имеется известный предал насыщении прослойка диафрагмами, при котором теплопроводная способность первого достигает минимума (после чего вновь повышается). Эго вытекает из представления об абсолютном пределе такого насыщения — о сплошном заполнении прослойка диафрагмами, следовательно о замещении 'в нем воздуха твердым веществом диафрагм,, более теплопроводным по предположе­нию, чем неподвижный воздух очень узких прослойков.

Рассмотренные выше операции деления воздушных прослойков а двух перпендикулярных направлениях дают в пределе результат, осуществляемый в природе в структуре высокопористых материалов, отличающихся поэтому наименьшей теплопроводностью.

3) Значение заполнения воздушных пустот каким-либо матери­алом. И здесь точное решение возможно в каждом отдельном случае путем вычислений: имея все данные для расчета общей теплопро­водности прослойка, а с другой стороны, зна. ч коэфициеит тепло­проводности заменяющего прослоек материала, можно определенно ■решить вопрос о выгодности или невыгодности этой замены в тепло­техническом отношении. При таких вычислениях выясняется вообще, что прослойки узкие, а именно ширины в 1—2 см (см. диаграмму "К. Хенки и шведских опытов на стр. 29), уместно засыпать только весьма квалифицированными терыоизоляторами (пробка, кизельгур)

или же ire засыпать новее; напротив, более широкие прослойки бывает,! выгодно засыпать н менее сильными термоизоляторами (торфяная |

мелочь, опилки и т. п.), а начиная с ширины в 10 см, их можно:|

засыпать почти всяким сухим порошком. Для облегчения практических!

>/ . f

расчетов зтого рода приводим выше таолицы для величины --- (тепло-?

сва {.

проводностн) п сбратных им (сопротивлений) у воздушных прослойков і при разной их ширине и разных величинах С'с; эти данные относятся { к вертикальным прослойкам н к горизонтальным при теплопередаче' последними снизу вверх.

При втом г. таблице Вирца принимают:

для теплых прослойков с — 1 „ пустот в стенах с = 0,9 в окнах c = 0,S

Пример. Выгодно ли засыпать сухим песком воздушный прослоек ши­риною 8 см в кирпичной кладке близ внутренней зоны? Из таблицы видны,

что теплопроводность прослойка, при величине С'с = 4 для кирпичной кладке

в теплой чести стены (сГ5г1), составляет по К. Хенки 4,89. Коэфициент теплопроводности >. для сухого песка по табл. 1 составляет 0,26, тепло-

0 ^6

проводность же слоя его в 0,08 л будет: = 3,8; или же, имея зна-'

чеиня для )/ в приложении VII, прямо сопоставляем оттуда >/ (==0,39) с X для песка (0,26).

Видны, что заполнение выгодно. При этом мы не' входим здесь в рассмо­трение привходящих практических обстоятельств, которые ».сгут влиять яг вывод, например вспрс са с том, совершенно ли сух весок и может ли оп сохраниться в такс м состоянии на будущее время и т. д. Равным образок ограничиваемся лишь указанием на крайнюю важность совершение плотных ограждеї ий воздушного слоя для устранения на практике ею п р о д у в а е г,! о с т и, которая может полностью нарушить его термоизоля­ционные свойства.

Для горизонтальных прослойков при теплопередаче сверху вин? имеем следующие сопротивления (по сводке Э. Шмидта):

Толщина прослойка в см

1

9

5 10 15

Как видим, они несколько выше предыдущих, что и понятно отпадения в этом случае конвекции воздуха. Из этого следует прочим, что наши обычные пустотелые потолочные перекрытия него этажа) несколько лучше защищают нас от летней жары, чем. зимнего холода (т. е. от у. течки теплоты зимой).

За последние годы новыми исследованиями.(W. МцІІ и Н. ЦеіЬег) намечены некоторые видоизменения в изложенных данных. Онц све_ деиы в нижеследующей таблице термических сопротивлений:

С практической точки зрения изменения, как видим, незначительны.

17. Если воздушный прослоек вентилируется, то ориентировочный рас­чет термического сопро­тивления как самого про­слойка, так и всей кон­струкции может быть произведен на следую­щих основаниях.

Взяв какой-либо при­мер такой конструкции (рис. 8), определим прежде всего темпера­туры X и у на границах воздушного прослойка,

если он замкнут [см. формулу (6), глава 1, часть I]: х — Тв— . -

~ Q у=Гв /г1 причем

1 -.т+2т

1

1 ' г

*гг

если через е и X обозначим толщины и коэфициенты теплопровод :ости слоев конструкции, расположенных ниже воздушного. прослойка, а че­рез г— термическое сопротивление прослойка.

З* I о’ з

Для дальнейшего расчета применяем метод пробного подбора вели­чии н последующей их проверки.

Предполагаем прежде всего, что речь идет о средних теплотехнических свойствах перекрытия, которые создаются по середине ската кровли. Взяв именно это ее место, задаемся здесь температурами л' п у', несколько мень­шими против предыдущих расчетов, и приступаем к проверке этого предпо­ложении.

Пусть для плоской крыши (рис. 8) имеем следующие задания: Тв — - f-15°, Тц = —30°: сечение прослойка 15X160 см при отверстиях 2X25 см, по 2 шт. вверху и внизу. Ограничиваемся практическим расчетом при постоянных коэфпниеитах.

При замкнутом прослойке имеем[12]:

fc=~r --------------------------- 1--------------------------------- =

1 1- 3 (дер) + у[13] (солом) + г (возд)

17,, II,, К

1

олз + одан-^ + з.^+ад.

Q, = и (15 + оО) = 19,8 кка. г,

—;+а4+мс-вж

■ ^ 0,15 О. Со

= —-—1------------ = о,52.

—— 4- 0.22 0,59 ^ ’

Тогда получим:

г VI ______________ і - * ip сто.

х-Тш~ Х>Г = Ь—-_д-_-18,5,

<?1 _ 15__

/:, ~ 0,52

г - „ - —18,5 — 23,1

Средняя температура воздушного прослойка будет ---------------- —-------- •= — 2U.8 .

При действии вентиляции средняя температура будет ниже найденной; для данного случая ограничиваемся в дальнейшем учетом лишь средней темпера­туры прослойка. После некоторых попыток выбираем ее равной—23° для середины ската. Действительно, при такой температуре имеем;

1) Фактический напор для вентиляции (по таблицам Браббе) для высоты (уклона) 10-0,1 = 1,0 м и разности температур с наружным воздухом в 7,0° — 0,082 мм вод. ст.

2) Расходуемый напор на трение совершенно ничтожен при очень малой скорости движения воздуха в прослойке (см. ниже); на местные сопротивления при Ї: = 4-1,0 = 4 он составит полученную выше величину 0,03 мм вод. ст - при скорости в отверстиях а, равной 0.35 м/сек, каковая и принята в расчет. Из этого видно, что скорость движения воздуха в самом прослойке будет

0.35 • 2 • 0.02 • 0.25

равна ------- 0~Ї5 "f о = 0,02 м/сек, что представляет весьма малую величину,

н потому сопротивление трепня такому потоку могло не учитываться.

Найди таким образом скорость потока в прослойке, при которой величина сопротивлений ему согласуется с имеющимся напором, получим теплопотерю через данную естественную вентиляцию в 1 час для 1 .я- прослойка в сере­дине ската.

2 • 0,02 • 0.25 - 0,35 • З С00 „ Q1 ,

'із =----------------------------------- кПцГ ’ ‘ = ' ккал'

Теперь пишем проверочное уравнение:

Q — бг + <7:ь /г, (15 + 23) = *,(15 + 23) + 2,7; 22,42 = 22,46.

из которого видно, что < но удовлетворяется ДОВОЛЬНО ТОЧНО. При численном определении *2 из k сохранено прежнее термическое сопротивление воздуш­ного прослойка 0,22, бывшее при его замкнутом состоянии. По ь данном слу­чае оно в не могло измениться существенно, поскольку уменьшение луче­испускании возмещается в известной мере усилением конвекции более холодными струями (в продольном и перпендикулярном к поверхности напра­влениях). Возможп.. впрочем и еще более точное решение с учетом этого изменения.

Таким образом окончательно устанавливаем температуру прослойка г, —23°. По этой температуре его нижней поверхности находим и теплопотерю пере­крытия:

Q' = А, (15 + 23) = 0,59 • 38 = 22,4 к кал.

Сравнивая полученную величину с тем, что f ы иуелн вначале для замкну­того прослойка, видим, что увеличение тепленотерн составляет около 1-1%. Таково же следовательно п увеличение коэфнцнента общей теплопередачи k I 20 4

ограждения I ~ --- 0,5 вместо прежней величины 0,44). В то же время

lo-j-ou J

видно, что новая его величина весьма близка к величине т. е. в силу в е II т и л я и и и прослойка почти полностью теряется терми­ческое сопротивление всех в и ш е л е ж а щ н х п а д н п ы слое в.

Предположим далее, что воздушный прослоек открыт как снизу, так и сверху всем своим поперечным сечением. Тогда отпадут отверстия а и вме­сте с ними почти все местные сопротивления; напротив, в силу увеличения скорости потока в самом прослойке получит значение сопротивление трения. Путем пробного подбора легко установить, что скорость потока, будет около 0,2 м/сек, а температура его около -—27°. Действительно, при этих значениях фактический напор будет 0,01ч мм во:, ст., а сопротивление трения па длине 10 м составит по таблицам (для эквивалентного круглого сечения равного 260 мм) ту же величину. Далее калорийная потеря на 1 м" будет:

0,15.0,2-3600

------------------------- ■----- . 0,31 * «J — /с/і і7.

а проверочное уравнение дает нам:

0,59 (15 + 27) = 0,52 (15 + 27) + 3,4,

т. е

24.78 = 25,24.

25

Коэфициент общей теплопередачи становится близким к —_-= 0,55, т. е.

45

к среднему между £[ и /’о. Иначе говоря, в этом случае для термо­изоляции перекрытия пропадает не только вся его часть выше воздушного прослойка, но и половина термического сопротивлении самого воздушного прослойка.

Конечно эти выводы относятся тслько к езятым условиям н заданиям, однако на них можно смотреть как на средние и приближенные в громадном большинстве случаев вентилируемых воздушных прослойков.

Более детальные расчеты воздушных прослойков с учетом тепло­передачи излучением и ветровых напоров см. у К. Ф. Фокина (см. спи­сок литературы). Однако следует заметить, что ветровые напоры, как фактор совершенно случайный, не должны входить в обычные расчеты; действн; же излучения нижней поверхности прослойка на верхнюю совершенно незначительно в данном случае в силу низких температур зимой и условий конвекции: входящий в прослоек холодный наружный воздух омывает главным образом нижнюю поверхность и тем пони­жает ее температуру.