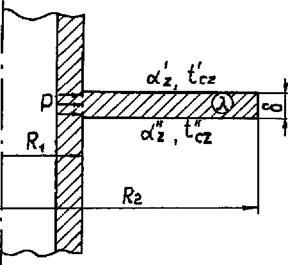
Круглое ребро постоянной толщины
На рис. 2.15 изображено круглое ребро, радиусы которого R}n R2, а толщина 5 ; поверхности ребра находятся в теплообмене со средой по закону Ньютона, причём со стороны верхней поверхности коэффициент теплообмена а, температура среды t'cz, а со стороны нижней поверхности эти параметры равны а"г, t"cz. Ha границе x = Ry в ребро входит постоянный поток Р, на границе х = Я2 теплообмен со средой настолько мал, что им можно пренебречь. Теплопроводность материала диска X. Требуется найти температурное поле диска.
|
Рис. 2.15. Круглое ребро постоянной толщины |
Задача сводится к решению уравнения (2.109), которое в нашем случае примет вид
2d2& dS l2 2n W-x2 + x b x& + ■
|
X |
|
(2.128) |
dx2 dx 3(x) = i(x) - іс:)ф
a z+a
|
a'+a'' |
xd~
Граничные условия
|
„ dS ■X — dx |
|
■2 — 1 dx |
|
x~Rx |
Сопоставив соответствующее (2.128) однородное уравнение с обобщённым уравнением Бесселя (2.123), находим
А=в=0 п=0 С=1 D2= b2
Используя обобщённое решение (2.124), получаем для соответствующего (2.125) однородного уравнения решение
&а = CXJ0 (ibx) + C2Y0(ibx) = C3I0(bx) + C4K0(bx),
Частное решение (2.128) имеет вид Зч=—- , тогда общее решение
уравнения (2.128)
3 = C3I0(bx) + C4K0(bx) + -^;
Ли
Сз и С4 найдём из граничных условий. Окончательно
Р (ЬКг )/0 (bx) + К0 (bx)Ix (bR2) [ W
2тгКхдХЬ I^bR^K^bR^-I^bR^K^bH,) ЛЬ2’ (2.129)
Приведём последнее выражение к форме, в которой фигурируют только безразмерные параметры:
м BiJXL±Xl. Rl Т,=,А;
р Х5 Р2 (2.130)
1 1 R2 , WSRj
~2Wl Цг)КМ + К,(г)1 .O',) + PBi