Дифференциальное уравнение теплопроводности для стержня
Температурное поле стержня или пластины может быть получено на основании решения соответствующего дифференциального уравнения для стержня или пластины вместе с граничными условиями. Такое уравнение обычно выводят специально, анализируя процесс переноса тепла в стержне или пластине. Однако оно может быть получено из общего уравнения Фурье, так как стержень или пластина представляют собою частные случаи тел с двух - и трёхмерным полем температур. Рассмотрим наиболее общий случай - анизотропное тело, все три размера которого имеют один порядок; пусть в теле равномерно распределены источники тепла удельной
о
мощностью W Вт/м. Стационарное поле температур в таком теле описывается дифференциальным уравнением (2.16) для параллелепипеда
. d2t d2t d2t
Для ограниченного цилиндра в стационарном режиме можно использовать
уравнение (2.8), положив в нём — = 0:
|
х ox ox dz dz |
дт
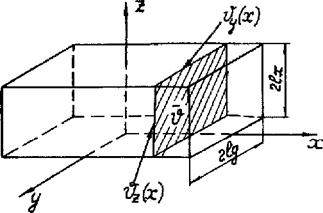
Рассмотрим сначала температурное поле параллелепипеда, на границах у = ±1 и z = ±l2 которого справедливы условия (2.24) третьего рода
(рис. 2.8):
|
.dt а і 1 (t — t ) dz Xу c |
|
+ -(t-te) ду Я |
|
= 0; |
|
:~±L |
|
У=±!у |
Обозначим t-tc = 9 и, в силу симметрии температурного поля, перепишем граничные условия в виде
|
d& > 2 |
|
d& dy 69 _ |
|
а) |
|
(2.92) |
|
у. О |
|
в) |
|
dz Л |
Условия на границах х = ±1х пока не оговариваем. Предположим, что градиент температур в данном теле в направлениях у и z мал и покажем, как можно учесть эту особенность температурного поля в дифференциальном уравнении (2.16), которое представим в форме
, d29 , d2& , d29 ттг п
|
(2.93) |
X —— + X —т - + X —— + W — о а*2 ' ay2 az2
Проведем над уравнением (2.93) следующую операцию:
к к
|
(2.94) |
|
yz |
[Л = ту f J fix, у, z)dydz,
I if V n n
у 2 0 0
т. е. умножим почленно уравнение на dydz и проинтегрируем его в пределах от 0 до 1у и /г, а затем разделим результат на произведение lylz.
Физически по отношению к 9{x, y,z) эта операция означает осреднение температурного поля в теле по направлениям у и z. Обозначим осредненное в направлениях у и z значение температуры (рис. 2.8 а)
|
(2.95) |
9(х) = 1У1 [5(х, у, z) = — J j Э(х, у, z)dydz.
* л п
y*z 0 0
Итак,
|
a%9. ax2' |
|
l_ yh 0 0 |
|
dy |
|
t rз a'i9, і rf3 a2f, , Vf/r^.,, ^ a7] = Tllr дґ^ = m[lwdy]dz |
|
.У z О 0 'у I. |
|
0 0 dy |
|
у z 0 0 |
|
|
|
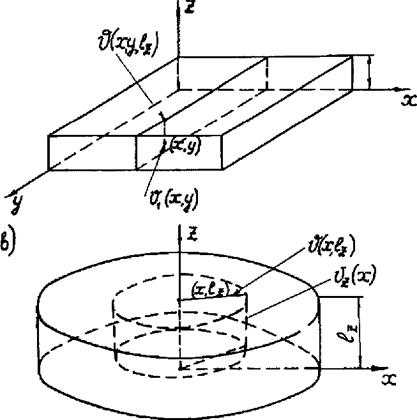
Рис. 2.8. К выводу дифференциальных уравнений параллелепипеда, пластины и стержня |
Поскольку в последнем выражении интегрирование и дифференцирование происходит по одной переменной у, то эти операции нельзя менять
местами. Рассмотрим интеграл
|
К = д$ О |
|
д& |
|
дЭ_ ду |
|
дЭ ду |
|
іду2 ' Joey^ |
|
dy=d — / І К ty) ду |
|
N! r |
|
>z). Л |
Последнее преобразование сделано на основании условия (2.92 а). Следовательно,
д2Я а Л ‘г сс
|
(2.96) |
К [Л ^т = ~JLJ~ f Wx, К >z)dz = —"■Я (х), }Л 2 ду2 ІілЛ і,
где
&z(x) = - j&(x, ly, z)dz - значение осреднённой по z температуры на
грани у=1у.
Аналогично проведём операцию lyz над третьим членом уравнения (2.93). Используем условия (2.92):
|
/¥ |
(2.97)
9y(x) = yWx, y,h)<ty,
*У О
«9 (х) - значение осреднённой по у температуры на грани z = /2.
[W(x, y, z)] = jj\ W(x, у, z)dydz = Wx).
Если W(x, y,z) = const, TO W =W.
|
д2$(х) ау |
Перепишем уравнение (2.93) с учётом преобразований
Лх _ ZZ. 9: (*) _ Ъ. $ (Х) + W' = О.
дх I, I у
Введём обозначения
Поясним физический смысл безразмерных параметров Ч*, и у¥у (см.
рис. 2.8 а).
Ч( -отношение осреднённой по z температуры на грани у = 1у к средней по сечению yz температуре. В общем случае Ч( и 4^ должны изменяться с х. Используя (2.98), перепишем последнее уравнение в следующем виде:
|
д23 ,2- W —— — й 3 ч — О, дх2 Ях Ь2 ay4,lz+a,4yl, ЛА |
|
а) (2.99) б) |
Если градиент температур по сечению yz стремится к нулю, то это означает, что средняя по сечению температура и температура на гранях iv
и lz стремятся друг к другу, т. е. ї ->1иТгч1. Тогда выражение для Ь2
примет вид
, aJ+azL
b (2Л00)
Уравнение (2.99), в котором Ь определяется по формуле (2.100), является дифференциальным уравнением для стержня с источником тепла.
Если стержень имеет периметр U и площадь поперечного сечения S, а теплообмен на границах происходит по закону Еіьютона с коэффициентом теплообмена а, то можно обосновать следующее выражение для b:
. 2 cdJ
ь =— (2.101)