Сложный теплообмен
|
|
Зависимости между тепловым потоком и разностью температур (ti~ ti) можно представить для кондуктивного, конвективного и лучистого механизмов переноса в единой форме:
(1.29)
где т - индекс, характеризующий механизм переноса (кондуктивный (:т=Т), конвективный (пг=К) и лучистый (т=Л));
Фі2т - тепловой поток между изотермическими поверхностями 1 и 2 для механизма m; tju t2- температуры изотермических поверхностей 1 и 2;
Ri2m - тепловое сопротивление потоку между изотермическими поверхностями 1 и 2 для механизма переноса т.
Если сопоставить формулу (1.29) с формулами для различных механизмов переноса, например, с формулами (1.5), (1.10), (1.14), то получаем следующие выражения для теплового сопротивления: кондуктивный перенос
Rl2T - R,
где R - тепловое сопротивление, определяемое по формуле (1.16), а для частных случаев плоской, цилиндрической и шаровой стенок - по формулам (1.22); конвективный перенос
(1.30)
|
(1.31) |
где ак - конвективный коэффициент теплообмена; лучистый перенос
ід = (^д^) і
где ал - коэффициент теплообмена излучением, структура которого дана формулой (1.11).
Если все три механизма переноса тепла существуют одновременно,
то тепловой поток Ф12 между изотермическими поверхностями 1 и 2 равен
Фі2 - Фі2К + Ф12Т + Фі2Л ; (1-32)
Заметим, что все приведенные здесь зависимости получены в предположении отсутствия стоков или источников энергии между изотермическими поверхностями 1 и 2. Расширим понятие теплопередачи от одной жидкой среды к другой через твердую стенку.
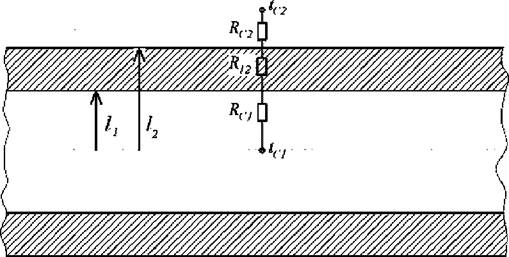
С этой целью рассмотрим перенос тепла в трубчатом теплообменнике, где жидкость с температурой tci, протекающая по трубе длиной L, нагревает жидкость с температурой tc2, омывающую наружную поверхность трубы (см. рис. 1.11).
|
Рис.1.11. К расчету теплового сопротивления трубчатого теплообменника |
На основании закона Кирхгофа тепловой поток от среды с температурой tcl проходит через стенку к жидкости с температурой tc2, преодолевая следующие последовательно соединенные тепловые
сопротивления: среда-стенка (Rci), стенка (R12) и стенка-среда общее
сопротивление потоку R равно:
R= Rc} + R]2 + Rc2 , (1.33)
где Rj2 - тепловое сопротивление простой или многосоставной стенки, определяется по формулам (1.22), (1.25), a Rc}, Rc2 равны:
Здесь а і и а 2 - полные коэффициенты теплообмена (конвективно - кондуктивный и лучистый) между средой и поверхностями стенок; АI =2жЫ] и А2 =2жЬІ2 - площади поверхностей 1 и 2.
Из формул (1.33), (1.34) следует, что
|
я 1 |
|
(1.35) |
|
2 J&. |
|
f 1 1,4 1 ^ , ц. _1П_£. 4-. |
|
■, <х/, А /, аг12 j |
Анализ формулы (1.35) приводит к выводу, что тепловой поток через отдельные сопротивления для рассматриваемого цилиндрического тела уменьшается непропорционально увеличению толщины изоляции. При
росте І2и неизменном 1} тепловое сопротивление —-—In— увеличивается, а
2я£Л /,
тепловое сопротивление —-—уменьшается. Такого рода двойной эффект
2^Zj£. /2 ^^2
означает, что для цилиндрической стенки существует определенный критический радиус 1кр, при котором потеря тепла является максимальной. Дифференцируя значение R из (1.35) по І2 и приравнивая производную нулю, найдем выражение для 1кр - критического радиуса изоляции:
. (1.36)
при котором будет наименьшее сопротивление R потоку.