Перенос тепловой энерГИИ кондукцией. Основные ПОНЯТИЯ и определения
Две системы могут обмениваться теплом лишь в том случае, если они находятся при различных температурах, причём перенос тепла происходит в направлении от системы с более высокой к системе с более низкой температурой.
Здесь не рассматривается вопрос о механизме переноса тепловой энергии кондукцией, конвекцией и излучением; основное внимание обращено на знакомство с феноменологическими законами переноса тепла. Количественные зависимости, связывающие разность температур систем с величиной теплового потока в случае кондукции, конвекции и излучения, имеют различный характер.
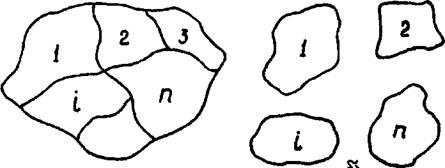
Рассмотрим перенос тепла кондукцией (теплопроводностью) в различных телах и системах тел. Совокупность тел с различными теплофизическими параметрами (коэффициент теплопроводности, объёмная теплоёмкость) и явно выраженными границами раздела будем называть системой тел или неоднородным телом (рис. 1.1).
|
|
|
S) |
|
Рис. 1.1. Системы тел. Неоднородное тело (рис а) |
|
ft) |
Каждая часть такой системы будет однородным телом. Однородные тела могут быть изотропными и анизотропными. В изотропном теле теплофизические параметры одинаковы во всех направлениях, в анизотропном - они различны в разных направлениях, но могут быть постоянными в выбранном направлении.
|
tm |
Тепловое состояние тела или системы количественно характеризуется его температурным полем, т. е. совокупностью численных значений температуры в различных точках системы в данный момент времени. В том случае, когда температура во всех точках системы не изменяется с течением времени, поле температур называется стационарным, если же температуры в теле с течением времени изменяются, то поле температур называется нестационарным (рис. 1.2).
|
|
Рис. 1.2. Изменение температуры во времени (иллюстративный пример)
Если температуры всех точек некоторого объёма равны между собою в любой момент времени, то это поле температур называют равномерным. Температурное поле в частном случае может зависеть только от одной координаты, тогда его называют одномерным.
Аналогичный смысл имеют термины двумерное и трёхмерное поле температур.
Если тела находятся при различных температурах, то, как указывалось выше, возникает поток тепла, направленный от тела с более высокой температурой к телу с более низкой температурой. Для количественного описания этого процесса вводят два основных понятия: изотермическая поверхность и градиент температуры.
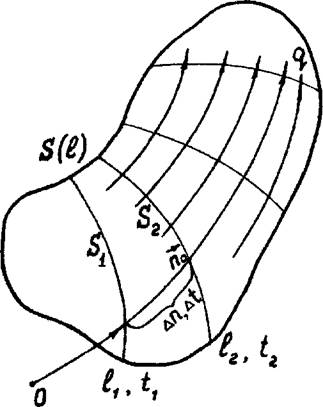
Изотермической поверхностью называют геометрическое место точек, имеющих одинаковую температуру. По определению, через каждую точку внутри тела можно провести в данный момент времени только одну изотермическую поверхность. На рис. 1.3 линиями Sj, S2 изображены следы на плоскости чертежа различных изотермических поверхностей в фиксированный момент времени.
|
Рис. 1.3. Изотермические поверхности и линии теплового потока |
Вдоль изотермы температура не изменяется, в любом другом направлении — изменяется, причём в направлении нормали к изотермической поверхности наблюдается наибольшее изменение температуры на единицу длины. Возрастание температуры в направлении нормали к изотермической поверхности характеризуется отношением изменения температуры At между выбранными изотермами к расстоянию между ними по нормали Ап. Предел этого отношения при устремлении Ап к нулю называется градиентом температуры (grad t).
Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры, т. е.
Hm = п — = grad t КУм (1.1)
а-оД п °дп v }
где Л0 - единичный вектор, направленный по нормали в сторону
возрастания температуры (рис. 1.3); — - производная температуры по
дп
направлению нормали.
За положительное направление градиента температуры принимают направление, в котором температура возрастает. Линии, перпендикулярные к изотермическим поверхностям, называют линиями теплового потока, или, короче, линиями тока. На рис. 1.3 эти линии обозначены стрелками.
В дальнейшем будем использовать следующие понятия:
- количество теплоты, Q, Дж;
- мощность источников тепла или тепловой поток (если рассматривается перенос тепла через поверхность)
Р = —, Вт; т - время, с; т
- поток на единицу площади
Р Вт
7 ~ ТГ’ Г S м
называется удельным тепловым потоком или плотностью теплового потока.
Основной закон, устанавливающий количественную связь между тепловым потоком и перепадом температур при кондуктивном теплообмене, называется законом Фурье по имени французского математика Ж. Фурье (1768 - 1830).
Плотность теплового потока прямо пропорциональна градиенту температуры, т. е.
— Qf
q = - Xgradt = - Я Vt = - ЛЯ0 —, (1.2)
дп
где X - коэффициент пропорциональности, называемый коэффициентом теплопроводности; grad, V - математические символы, обозначающие градиент.
В математике положительное изменение функций направлено в сторону возрастания функции. В рассматриваемом случае тепловой поток направлен в сторону убывания температуры. Чтобы устранить противоречие между математическим и физическим определением положительного направления функции в зависимость (1.2) вводится знак «-».
Соотношение (1.2) является обобщением опытных данных и лежит в основе всей современной теории теплопроводности.
Выражение (1.2) можно представить в виде суммы составляющих градиента по осям декартовых координат
, - dt - dt 7 dt
gradt ~i — + j — + k — , (1.3)
ox 8y 6z 47
где г, j, к - ортогональные между собою единичные векторы, направленные по координатным осям.
Рассмотрим неизменное во времени |^ = 0| одномерное поле
дт )
температур, изменяющееся лишь в одном направлении х. Математическая формулировка этих условий имеет вид
TOC o "1-5" h z dt dt dt dt
— = — = 0; — 0; — = 0
dy dz dx dr
Пусть, кроме этого, градиент температур — будет постоянной
dx
|
const, где tjK t2- значения температур на поверхностях х/и х2 |
величиной, т. е. температура линейно изменяется с координатой х, тогда dt _ t2- tx
dx х2 ~xl
.причём tj> t2 , х2. > хі.
Величину плотности теплового потока q можно определить по формуле, которая следует из (1.2),
/л л
Ч. ^ 5 (1.4)
А т х2 - хх
Из (1.4) запишем выражение для коэффициента теплопроводности
Q х2-х1
X :
Ат tx-t2
т. е. коэффициент теплопроводности равен плотности теплового потока при перепаде температур на единице длины нормали, равном одному градусу. Размерность коэффициента теплопроводности в системе Си - Вт/м-К.