Тепловое аккумулиров ание энергии

Аккумулирование со скользящим давлением

Аккумулирование при скользящем давлении (аккумули­рование при переменном давлении, аккумулирование пара) с разрядкой насыщенным паром осуществляется с использо­ванием разрядной линии 4 на рис. 2.2. Резервуаром аккуму­лятора обычно служит теплоизолированный сосуд под дав­лением. Около 75—95 % объема сосуда заполнено водой в со­стоянии насыщения, тогда как от 5 до 25 % объема занято паровой подушкой.

Процесс разрядки начинается с открытия клапана на раз­рядной линии. Паровая подушка обеспечивает разделение фаз. При этом насыщенный или влажный пар с очень не­большим содержанием жидкости (обычно менее 1 % по массе) покидает резервуар.

Вследствие высокой энтальпии пара во время разрядки испаряется сравнительно малая доля жидкости; основная ее часть остается в сосуде при более низкой температуре.

Для того чтобы избежать температурного расслоения воды по объему при зарядке и разрядке и обеспечить необ­ходимую циркуляцию, устанавливаются специальные внут­ренние устройства 12, что особенно важно для вертикальных сосудов (разд. 4.2).

Зарядка обычно осуществляется продувкой насыщенного или перегретого пара несколько более высокого давления че­рез жидкость, вследствие чего в резервуаре под действием эжекции и массовых сил возникает циркуляция [2.3]. За­рядка также возможна через теплообменную поверхность с использованием пара, имеющего более высокую темпера­
туру, чем жидкость, например за счет конденсации насыщен­ного пара более высокого давления или охлаждения перегре­того пара достаточно высокой температуры (и даже более низкого давления — с использованием «трансформатора пара»).

Разрядка резервуара аккумулятора такого типа всегда сопровождается значительным понижением давления (а за­рядка— соответствующим повышением). Поэтому такой тип аккумулирования называется аккумулированием со скользя­щим давлением (в отличие от систем аккумулирования с по­стоянным давлением). Иногда его называют именем Рутса в честь изобретателя Дж. Рутса, который внедрил эту си­стему в 1920-х гг. в различных отраслях промышленности, а также на тепловых электрических станциях.

К достоинствам этой системы относятся быстрота подго­товки к работе, сравнительно низкие капиталовложения, пря­мое питание и зарядка паром. Возможности дальнейшего применения систем такого типа связаны с разработкой новых технологий изготовления сосудов давления и соответственно новых гидравлических схем аккумуляторов. Подобные си­стемы теплового аккумулирования были также предложены для больших естественных подземных хранилищ (разд. 4.4).

Разрядка такого аккумулятора описывается уравнением (2.6), где йтвх — 0 и, в качестве приближенного условия, dVак = 0. Для насыщенного пара уравнение (2.6) принимает вид

НСр Л/77вых AQ — Л (Пак/77ак)>

где Л обозначает конечные разности, например Л (иак1Пак) = (ЫакТИак)к (Цак777ак)н-

Здесь н — начало процесса (разрядка), к — конец процесса, " — насыщенный пар.

Индекс «ср» в уравнении (2.8) относится к среднему зна­чению энтальпии. Для очень малых приращений h"p = h" +

Уравнение баланса масс (2.7) сводится к Л/«вых = Л/71ак == tflaK. K Т71ак, н-

Уравнение (2.8) не может быть решено непосредственно, если влиянием объема пара в сосуде нельзя пренебречь. В та­ких случаях (например, при высоком давлении) нужно учи­тывать не только массовую долю воды при и', но и массовую долю пара при и":

иак =* и' (т'/так) + и" (m'7maK).

Из баланса объемов

VaJmaR = v'm'lmaK + v"m"/maK (2 Л 2)

и баланса масс

так = т' + т" (2ЛЗ)

можно определить влагосодержание

TOC o "1-5" h z т'/так= 1 — т"Ітак (2Л4)

и паросодержание

m"/maK = {VJmaK — v')/(v" — v'). (2Л5)

Тогда уравнение (2Л1) принимает вид

uaR = u' + {VJmaR — v'){u" — u')/(v" — v'). (2Л6)

Правая часть уравнения состоит из части, определяемой че­тырьмя интенсивными переменными состояния, и экстенсив­ной части.

С учетом

j = u'-v'(u"-u')/(v"-v') (2Л7)

уравнение (2Л6) преобразуется в

«ак = /ак + (VJmaR)(u" — u')l(v" — v'), (2.18)

а уравнение аккумулирования (2.8) принимает вид

Н Д«?вых == (/ак«1ак)н (/ак«^ак)к “Ь + + <2|9>

или с учетом уравнения баланса масс (2.10)

(ЛСр /ак, к) Д^вых === (/ак, н /ак, к) ^ак, н 4“

+ l',«[(v^)H-(-^^)J + 4Q = a + 6 + c. (2.20)

Обычно, во всяком случае для движущихся сред, вместо внутренней энергии и используется энтальпия h. С помощью уравнения (2.5) и

r = h" — h', (2.21)

w = v" — v' (2.22)

получаем

U" - и' _ (/і" - h') - р (и" - у') г__________________________

v" — v' v" — v' ~w р (г. гй)

и /ак = [«' - V (и" - и'Щак = (Л' — v'r/w)№. (2.24)

Тогда уравнение (2.20) можно переписать так:

(^ср /як* к) Л/Лвых (/ак* н /ак. к) ^ак. н “Ь

+ у ак [(/-/ш)н — (г/ш)к — (р„ — рк)] + AQ = а + 6 + с. (2.25)

Таким образом, уравнение аккумулирования [(2.20) или

(2.25) ] описывает:

— изменение количества энергии в аккумулирующем ре­зервуаре (с учетом объема пара в нем) путем использования / вместо и соответственно слагаемому а и дополнительному слагаемому 6;

— подведенное тепло (например, путем аккумулирования его в стенках резервуара и/или через дополнительную тепло­обменную поверхность) минус тепловые потери, описывае­мые членом с.

Это уравнение вывел в 1933 г. Гилли [2.4] и дополнил Бекман [2.5, 2.6] введением члена, учитывающего расшире­ние аккумулирующего сосуда. Хардеген [2.7] рассмотрел также влияние не полностью дегазированной воды.

При решении уравнения аккумулирования для случая из­менения состояния от «н» до «к» (например, от рк до рк) предполагаются малые приращения р и оценивается выход массы Д/Пвых. Для следующего шага так, н уменьшается на

ЛШвых-

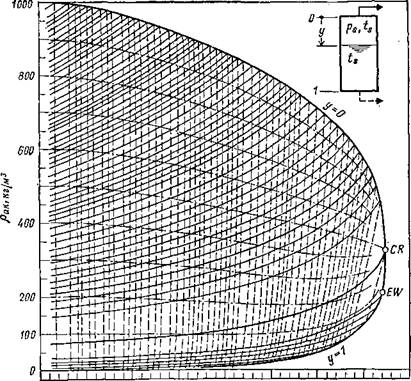
На рис. 2.3 показана зависимость удельной массовой ак­кумулирующей емкости пароводяной смеси от давления на­сыщения ps или температуры насыщения ts в качестве пара­метра выбран относительный объем пара у.

Состояние в начале разрядки («н») обычно определяется параметрами рн и ун. Таким образом, сразу же можно найти рак н - Разрядка представлена кривыми, ниспадающими до конечного давления рк. Индекс «к» определяет плотность и объем пара в конце разрядки. Выход пара на единицу объема аккумулирующей емкости (удельный расход пара) определяется выражнием Драк = рак, н — рак, к.

На этой диаграмме верхняя ограничивающая кривая пред­ставляет собой плотность воды в состоянии насыщения р', а нижняя — плотность насыщенного пара р". Из диаграммы становятся очевидными пределы увеличения аккумулирую­щей емкости (при данном давлении разрядки) с повышением давления при зарядке: энтальпия увеличивается постепенно, а плотность снижается существенно быстрее.

Рис. 2.3 построен по уравнению (2.25) и таблицам пара [2.8]. При этом подвод или отвод тепла от внутренней по­верхности резервуара [что соответствует члену с в уравнении

(2.25) ] не рассматривался. Однако аккумулирующая емкость сосудов высокого давления заметно увеличивается вследствие теплоемкости стенок сосуда [1.18]. Приближенно этот эффект

Рис. 2.3. Зависимость плотности запасаемой энергии от температуры (дав­ления) насыщения для аккумулятора со скользящим давлением.

* - разрядка насыщенным паром; разрядка насыщенной водой; CR — кри­тическая точка; EW — конец разрядки водой; у — относительный объем пара. При­мер для разрядки паром: начало разрядки Рн=*6,0 МПа (<н=*275вС), Ун^0,10; конец разрядки рк= 1,0 МПа (= 180“ С); результаты рак н=685 кг/м1, раК к=535 кг/м3, Ук=0,60; расход пара Драк=*685—535=150 кг пара на 1 м3 объема аккумулятора.

может быть учтен, если принять объем стенок сосуда за до­полнительный объем воды, так как объемные теплоемкости стали и воды практически одинаковы.

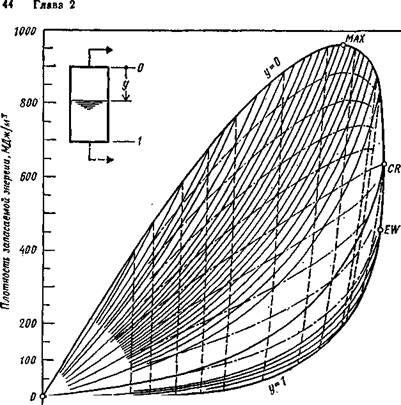
На рис. 2.4 показана диаграмма удельной емкости акку­мулятора системы теплового аккумулирования со скользя­щим давлением. Верхняя кривая имеет максимум примерно при 12,7 МПа. Более высокие давления, таким образом, для простого теплового аккумулирования неэкономичны. Однако

Рис. 2.4. Зависимость плотности запасаемой энергии от температуры (дав­ления) насыщения для аккумулятора со скользящим давлением.

Обозначения и пример те же, что для рис. 2.3. Плотность запасаемой энергии 830— 410-420 МДж/м3.

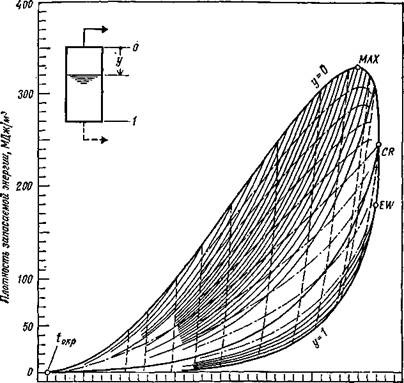
если аккумулирование осуществляется на тепловой электро­станции, то оно становится уже аккумулированием не просто массы или тепла, а располагаемой энергии (эксергии). На рис. 2.5 показана удельная емкость системы аккумулирования эксергии (плотность запасаемой эксергии) для температуры окружающей среды /окр=10°С (283 К), соответствующей давлению насыщения 1,2 кПа. Действительно, оказывается, что имеет смысл использовать высокое давление на тепловых электростанциях (максимум плотности аккумулируемой эк­сергии достигается только примерно при 17 МПа или при 352 °С).

Ps, МПа

Рис. 2.5. Зависимость плотности запасаемой эксергии от температуры

(давления) насыщения для аккумулятора со скользящим давлением.

Обозначения и пример те же, что для рис.2.3. Плотность запасаемой эксергии 240- 85 = 155 МДж/м3.

Для аккумулятора со скользящим давлением, который разряжается перегретым паром (линия 5 на рис. 2.2), при­менимы уравнения (2.20) и (2.25) при условии, что принята соответствующая энтальпия перегретого пара для h'c'.