Сварные конструкции. Расчет и проектирование
РАСЧЕТ ЖЕСТКОСТИ И ПРОЧНОСТИ БАЛОК (ПОДБОР СЕЧЕНИЙ)
Балка должна удовлетворять требованию жесткости, т. е. ее прогиб /го„ от наибольшей нагрузки не должен превышать предельно допускаемый. Обычно в балках предельное значение отношения /го„// регламентируется нормами. Норма жесткости для балок разного назначения различна, например в подкрановых балках /Ш1х//<1/600. . .1/700; в главных балках междуэтажных перекрытий /„„//<1/400.
Чтобы удовлетворить требованиям жесткости, балка должна иметь высоту не менее некоторой предельной. Эта минимальная высота определяется видом нагружения и допускаемыми напряжениями. Рассмотрим, какова должна быть наименьшая высота балкн, свободно лежащей на двух опорах, если она нагружена равномерной нагрузкой q (рис. 9.3, о).
Расчетный прогиб в середине пролета
|
(9.1) |
_5_ ?/« 384 EJ '
где EJ — жесткость балки.
Для рассматриваемой балкн расчетный момент
|
|
(9.2)
Подставляя значение М в формулу (9.1), получим
|
(9-3) |
5мі* . ' 48£7 '
изгибающий момент
где (о]р—допускаемое напряжение; W — момент сопротивления.
|
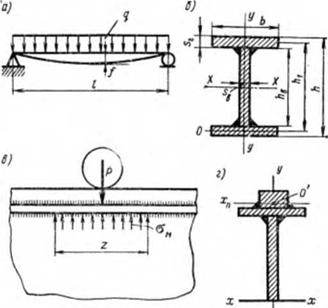
Рис. 9.3. К расчету сварной балки: а — изогнутая ось балки от а; 6 — поперечное сечение балки; а. а — влияние со - средоточенкой силы |
Если расчетное сечение симметрично относительно
•2 У
горизонтальной оси, то W где h — высота балки.
Подставим значение М из формулы (9.2) в формулу
(9.3):
(9.5)
|
откуда |
24 £Л ’
|
(9.6) (9.7) |
/ _ 5 [о|р/
|
или |
/ — 24£Л »
Л 5 |о]р/
/ 24ЇЇГ *
|
Тип конструкции |
т |
|
Подкрановые балкн и фермы: |
1/500 |
|
при ручных кранах |
|
|
при электрических кранах грузоподъемностью |
1/600 |
|
до 50 т |
1/750 |
|
при электрических кранах грузоподъемностью |
|
|
свыше 50 т |
|
|
Монорельсовые пути |
1/400 |
|
Балки рабочих площадок производственных зда |
|
|
ний: |
1/400 |
|
главные при отсутствии рельсовых путей |
|
|
прочие |
1/250 |
|
Балкн междуэтажных перекрытий: |
1/400 |
|
главные |
|
|
прочие |
1/250 |
Высота балки, вычисленная по формуле (9.7), является наименьшей при заданных [<т]р и f/l и может быть увеличена, если это диктуется соображениями компоновки конструкции или экономии металла. При других нагружениях и системах балок, например консольных, многоопорных с защемленными концами и т. п., в формуле (9.7) изменяется лишь числовой коэффициент ер,. В общем случае
Л = Фо HW - (9.8)
Балки из стали СтЗ для различных элементов конструкции могут принимать следующие предельные отношения fit (табл. 9.1).
При действии моментов в вертикальной Мх и горизонтальной Ми плоскостях должно удовлетворяться требование (охЧ-а„)<[а)р.
Балка должна удовлетворять прочности при условии наименьшей массы, т. е. поперечное сечение должно быть минимальным.
Высота балки для двутаврового профиля с этой целью может быть найдена по формуле
а для коробчатого _____
где s„ — толщина вертикального листа.
При проектировании балок толщина s„ в формулах (9.9) и (9.10) неизвестна. Поэтому ее первоначально задают. Для разных строительных конструкций s. обычно изменяется в сравнительно узких пределах (рис. 9.3, б).
Можно принимать sB=5. . .10 мм
ь-Чг?; (9П)
для тяжелых конструкций
s. = 7 + 0,005ft., (9.12)
где 5. и Л. выражены в миллиметрах (рис. 9.3, б).
Значения Л, найденные с учетом требований достаточной жесткости и прочности, а также при условии наименьшей массы, могут оказаться совершенно различными. Из двух значений, вычисленных для балки двутаврового профиля по формулам (9.7) и (9.8) или (9.9) и (9.10), следует принять большее и во всяком случае не меньшее, чем при вычислении по формулам (9.7) и (9.8).
Далее подбирают размеры поперечного сечения балки с учетом расчетного и изгибающего момента М и высоты А.
Рассмотрим процесс подбора сечения двутаврового профиля (рис. 9.3, б). Для этого найдем требуемый момент сопротивления
и требуемый момент инерции сечения
РТ - <9-14)
Вычислим момент инерции У. вертикального листа вы
сотой А. и толщиной s.. Принимаем А„=0,95Л.
Находим требуемый момент инерции двух горизонтальных листов:
Л = 7Т,-У.. (9.15)
В другой форме момент инерции выразится так:
Уг = 2[ув-Мг(^)?], (9.16)
где У»—момент инерции горизонтального листа относительно собственной оси, который всегда очень мал и может быть принят равным нулю; Л, — расстояние между центрами тяжести горизонтальных листов, которое можно принять равным (0,96. . .0,98)А.
Из уравнения (9.16) находим требуемую площадь сечения одного горизонтального листа:
Ат — Цт - (9-17)
Пі
Подобрав размеры поперечного сечения балки, определим напряжения и таким образом проверим, удовлетворяют ли подобранные размеры условиям прочности. Напряжение от изгиба
(9.18)
Касательное напряжение от поперечной силы будет t=Si. (9.19)
где Q — наибольшая поперечная сила балки; S — статический момент полуплощади сечения (симметричного) относительно центра тяжести балки (рнс. 9.3, б).
Эквивалентные напряжения проверяются обычно в тех случаях, когда максимальные значения ант совпадают по длине балки в одном сечении. Их определяют на уровне верхней кромки вертикального листа:
<т. = К5{ТЗЇЇ. (9.20)
Из формулы (9.20) имеем нормальное напряжение
= (9.21)
касательное напряжение
т,-4Ь, (9.22)
где S, — статический момент площади горизонтального пояса относительно центра тяжести сечения балкн.
В большинстве случаев эквивалентные напряжения аэ оказываются меньше о, вычисленного по формуле (9.18).
Допустим, что к верхнему поясу балки прикладывают сосредоточенные перемещающиеся грузы (рис. 9.3, в). Эго имеет место в крановых, подкрановых и мостовых балхах. При этом определяют прочность вертикального листа с учетом местного напряжения под грузом: где rn — коэффициент, который имеет различные значения, т= 1,4. . .1,5 — при тяжелом режиме работы балки (например, в металлургических цехах); т— 1—при легком режиме (в ремонтных цехах и т. п.); z — условная длина, на которой сосредоточенный груз распределяется в вертикальном листе (рис. 9.3, в):
г = 3,25 І/ї. (9.24)
V 5ц
Здесь Уп — момент инерции горизонтального листа совместно с приваренным к нему рельсом (если таковой имеется) относительно оси х„, проходящей через их общий центр тяжести (рис. 9.3, г).
При наличии программы легко с помощью ЭВМ определить размеры поперечного сечения проектируемой балки, обеспечивающие минимум массы металла и требуемую жесткость при изгибе.