Сварные конструкции. Расчет и проектирование
ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ УСИЛИЙ О БАЛКАХ МЕТОДОМ ЛИНИИ ВЛИЯНИЯ
Расчетные усилия в балках часто удобно определять методом линий влияния. Этот метод особенно целесообразен при нахождении усилий в балках от движущихся систем грузов, которые могут занимать различные положения на изучаемой конструкции, например от веса тележек, перемещающихся по балкам крана.
Аетод линий влияния принят при расчете не только балок, но и ферм, рамных конструкций и особенно при
расчете мостов крановых и других инженерных сооружений.
Линия влияния выражает зависимость усилия (или деформации) в каком-либо заданном сечении балки или элементе фермы от положения груза в них. Линии влияния в практических расчетах всегда строят от одного груза,
|
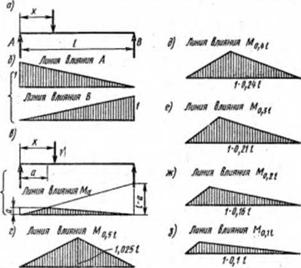
Рис. 8.5. К построению линий влияния опорных реакций и М в разных сечениях балки |
равного единице, и после этого построения ее используют для определения усилий (или деформаций) в изучаемом сечении или элементе при любом заданном загруженнн от нескольких сосредоточенных сил или распределенных нагрузок
Линии влияния опорной реакции и однопролетной балке с шарнирными опорами. Линия влияния опорной реакции балки выражает зависимость величины реакции от положения груза, равного единице, на балке.
Обозначим расстояние груза до левой опоры через х, пролет балки через / (рис. 8.5, а).
Реакция А = 1 1~- .
Реакция А определяется уравнением наклонной прямой (рис. 8.5, б):
при лг=0 /4 = 1;
при х~1 /1=0.
Подобным же образом строится линия влияния реакции В (рнс. 8.5, б).
Линия влияния изгибающего момента М выражает зависимость величины момента в заданном сечении от положения груза, равного единице, на балке.
Допустим, что груз находится справа от сечения. При этом изгибающий момент
Ма — Ла=
Построим линию влияния момента М (рнс. 8.5, в) из условия, что: при х—0 Ма — а x—l ;Vfo=0.
Так как было сделано предположение, что груз находится справа от сечения а, то построенная прямая верна лишь на участке / — а.
Допустим, что груз находится слева от сечения а.
Изгибающий момент целесообразно выразить в этом случае через величину правой опорной реакции:
Мв = в(/-а) = 1|(/-а).
При х=0 М„=0; при х—1 Ма—1 — а.
Так как было предположено, что груз находится слева от а, то построенная прямая верна лишь на участке / — а.
Линия влияния Ма имеет форму треугольника, заштрихованного на рис. 8.5, в, с вершиной в сечении а.
Если линия влияния строится для сечения 1/2, то вертикальные отрезки, откладываемые на опорах, равны
между собой и равны 1 . Высота треугольника в этом
случае равна 1 (рнс. 8.5, г).
Подобным образом линии влияния М строятся для разных сечений балки, например 0,4/, 0,3/, 0,2/, 0,1/ (рис. 8.5, д. . .з). Ординаты линнй влияния М имеют размерность длины. Высоты треугольников равны 1 -0,25/; 1-0,24/ и т. д.
Линии влияния поперечной силы Q. Линии влияния поперечной силы Q выражают зависимость величины поперечной силы в заданном сечении а от положения груза, равного единице, на балке.
Допустим, что груз находится справа от сечения а:
|
|
Построим эту линию из условия (рис. 8.6, я), что
при д:=0 <?а = 1;
при х=1 Qa=0.
Прямая верна на участке / — а.
Допустим, что груз находится слева от сечения а. При этом
Qa~ — В = — 1 у
при ЛГ=0 Qa=0'.
при X=l Qa—— 1-
|
сечением она меняет знак. а) |
Эта линия верна на участке а — /, под исследуемым
|
а |
’)
Линия 1/тлт ■ ^^ШППїїїїПїїППГГ-т,..
|
ЛЯЯЯ /юЯШЯ вд ^дд^ГСіїШГмтіттптгг^^ |
|
^ Линия Ймяния 4t, ft V |
Линия 1/шшя 1^1ЛїШЇЇПТЇЇТ1ЇЇПїїттт~^
Ч Линия ішния
|
I) Линия t/юянин |
Линия шяний Цд
_^ртшптттттл 1,0 ДТММ^
Рис. 6.6. К построению линии влияния Q в балке
Линии влияния Q для сечений балки 0,5/, 0,4/, 0,3/, 0,2/, 0,1/ и опорные показаны на рис. 8.6, а. . .ж. Ординаты линий влияния Q безразмерны.
Рассмотрим, как строятся линии влияния М и Q для балки, защемленной в стену (рис. 8.7, а. . .г).
В сечении на свободном конце М, н Q, всегда равны нулю, в каком бы месте ни находилась единичная сила на балке. Поэтому линии влияния для этого сечения являются нулевыми (рис. 8.7, а). В сечении по опоре М0——1 • дг, т. е. линия влияния имеет вид наклонной прямой. При х=0, т. е. когда сила находится в опорном сечении, Af0=0
при х=»/ (груз на конце консоли), М=—I/ (рнс. 8.7, б).
|
ь |
|
- |
|
a) t - ЛІЛ Mr О jfc ff’S—
l) it —„Л* i/t Рис. 8.7. К построеии» линий влияния защемленной в стену (а, б, в) и консольной (г) балок |
Поперечная сила в опорном сечении Qn=—1 в каком бы сечении балки ни находился груз (рис. 8.7, в).
Задание 1. Построить линии ВЛИЯНИЯ М//, И Q//, для середины пролета балки, защемленной в стену (рис.8.7, а).
Задание 2. Построить линии влияния Mi, г и Q//, для середины пролета консольной балки, у которой расстояние между опорами /, а длина консоли равна 1/4 (рис. 8.7, е).
Задание 3. Построить линию влияния Qo для опорного сечения той же консольной балки. Сечение смещено на <Lr в сторону консоли.
Задание 4. Построить линию влияния Q для опорного сечения той же консольной балки. Сечение смещено на dx в сторону междуопорной части (рис. 8.7, г).