Сварные конструкции. Расчет и проектирование
ОБРАЗОВАНИЕ И ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ ПРИ СВАРКЕ
|
|
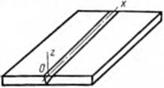
Основные понятия и классификация. В теории сварочных деформаций и напряжений принято использовать расположение осей координат, показанное на рнс. 6.1. Ось Ох направлена вдоль шва; Оу — поперек шва в плоскости пластины; Ог — поперек шва в направлении толщины. Соответственно различают напряжения оя, Оу, ог, хХу, т, я; деформации е*. ву, ег, ухи,
Уяи Уtx и перемещения точек JL тела и по оси Ох; и — по оси
Оу; и/ ___ ПО ОСИ Ог. Рис - 61- Расположение коор-
Расширение и сокращение динатных осей в пластине
металла от неравномерного
нагрева или охлаждения, а также от структурных превращений образуют так называемые собственные или внутренние деформации и напряжения при сварке. В отличие от напряжений и деформаций, создаваемых нагрузками, собственные напряжения в деформации существуют в теле при отсутствии каких-либо нагрузок.
Собственные напряжения —это такие напряжения, которые существуют в теле при отсутствии приложенных к нему поверхностных или объемных (инерционных, гравитационных) сил.
Чтобы более ясно понимать причины образования собственных напряжений, рассмотрим различные виды деформаций металла.
1. Температурные деформации еа вызваны изменением размера частиц тела при изменении температуры. К температурным деформациям условно относят также деформации, возникающие в процессе структурных превращений:
еа = аТ, (6.1)
где а — средний коэффициент линейного расширения в интервале изменения температуры от 0 до Т, включающий в себя и влияние структурных превращений, °С'1; Т — изменение температуры в какой-либо точке тела, °С.
Сдвиговые температурные деформации уа в изотропных телах не возникают.
2. Н а б л ю д а е м ы е деформации ен и у„ характеризуют изменения размеров тела — линейных и угловых, которые можно зарегистрировать измерительными приборами. В теории упругости и пластичности нх называют деформациями, не присваивая нм никакого индекса.
3. Собственные (внутренние) деформации состоят из упругих e^,v, Yynp и пластических еиЛ, у„д.
Указанные виды деформаций связаны между собой следующими соотношениями:
P| = fynp *Ь ®пл 4" ®а> (6.2)
Yu 3 Yynp 4" Yai - (6.3)
Если до процесса нагрева или охлаждения в точке тела возникли начальные пластические деформации е„ и у„
* ПЛ Ил *
вызванные предшествующими деформациями, то формулы
(6.2) и (6.3) примут следующий вид:
= супр 4" Д^ш + е0 -+■ ®enji; (6.4)
Yi= Yynp + Дупл + Y«nj> (6.5)
где Депл и Дуод — приращения пластических деформаций на стадии рассматриваемого процесса.
Собственные напряжения классифицируются по различным признакам. По причине, их вызвавшей, они делятся на напряжения: от упругого или пластического механизма деформирования при сборке, монтаже и правке; от упругих и пластических деформаций из-за неравномерного нагрева деталей; от неравномерного изменения объема тела при фазовых превращениях. По времени существования они могут
быть временными, существующими в период выполнения технологической операции или протекания физического процесса, и остаточными, устойчиво сохраняющимися в течение длительного периода. Собственные напряжения бывают одноосными (линейными), двухосными (плоскостными) и трехосными (объемными). В зависимости от объема, в пределах которого напряжения взаимно уравновешены, они называются напряжениями первого рода (макрообъем), второго рода (зерно) и третьего рода (кристаллическая решетка).
Собственные напряжения первого рода могут быть выражены через упругие деформации:
~ 20 ( %пР + 7=5|Г с*); = 20 ( %.Р + -ПЛЇГ «•):
°* = 20 ( е*Упр + в° )'
|
*Pynp’ ТР* = = gYpw |
|
= Оу. |
|
где G — |
|
2(14-ц)' |
|
(6-6) ®*упр”^” е0улр 8*уир |
Свойства металлов при высоких температурах. Для
вычисления собственных напряжений довольно часто приходится использовать характеристики свойств металлов при высоких температурах.
|
Таблица 6.1 Теплофнзические свойства некоторых металлов
|
|
* Средний коэффициент линейного расширения а' в ди»пааоы< температур 0. . .1000 "С. при определении которого исключено сокращение металла вследствие структурного превращении. |
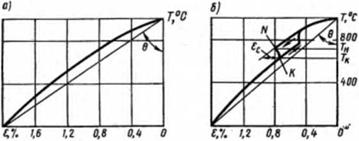
Теплофизические характеристики, такие, как объемная теплоемкость су, теплопроводность л и температуропроводность а, берут обычно средними в необходимом интервале температур. В табл. 6.1 указаны их значения для случая сварки металлов. Коэффициенты линейного расширения а также обычно берут средними в некотором диапазоне температур. Однако в ряде случаев приходится пользоваться дилатограммами — экспериментально полученными графиками изменения линейного размера образца оттемпературы (рис. 6.2). В металлах, не испытывающих структурных
|
Рис. 6.2. Дилатограммы металлов без структурных превращений (а) и со структурными превращениями (о) |
превращений, изменение длины образца происходит монотонно (рнс. 6.2, а), поэтому используют не мгновенное значение a=de/dT, а принимают а=е/7'—tg 0. В металлах со структурными превращениями, например в углеродистых и легированных сталях, график имеет сложный характер (рис. 6.2, б). При охлаждении металла от максимальной температуры нагрева до точки N — начала структурного превращения — происходит монотонное сокращение образца, а затем, несмотря на снижение температуры, его удлинение. После завершения структурного превращения (точка К) образец вновь начинает сокращаться. Положение точек начала Т„ и конца Тн структурных превращений зависит от химического состава металла и термического цикла охлаждения (скорости охлаждения). Чем выше скорость охлаждения, тем ниже Т„ и Тк. От состава металла и скорости охлаждения зависит также деформация структурного превращения ес.
В расчетах сварочных деформаций и напряжений часто используют коэффициент а и обобщенную характеристику а /су. В приближенных расчетах, не связанных с учетом структурных превращений, достаточно пользоваться сред
ними значениями а (см. табл. 6.1). Обобщенная характеристика a/су мало изменяется в зависимости от температуры. На рис. 6.3, а, б показаны для низкоуглеродистой и для
|
aio't/fc |
|
по т |
a to* i/к м
|
а |
Г°~' |
||||||||
|
К" |
г» |
V-» |
|
20 /6 к |
|
по *то 670 V с у, Дм/(ск) |
|
870 №70 |
|
(с/ |
Шер |
к, |
I |
А |
|||
|
і |
ш |
Ш |
И |
и |
|
: |
|
670 |
|
870 НПО |
|
Рис. 6.3. Зависимости а, су и а/су от температуры: аср. (су)ср и (а/су)ср — средние значения от Т-270 К до соответствующей температуры Т: а — ииікоутлероднстля сталь тип» СтЗ; 0 — хромо - никелем» сталь тип» 18-8 |
хромоникелевой стали типа 18-8 зависимости а, су и а/су от температуры, вычисленные как средние значения в диапазоне от Т—270 К до соответствующей температуры Г.
с, мп а
|
0 100 200 300 m500 S00 Т'С |
|
Рис. 6.4. Зависимость модулей упругости Е, О и козффнцнента Пуассона |1 от температуры для стали 25 |
|
|
|
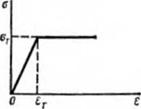
Рнс. 6.5. Диаграмма зависимости Напряжения от деформации для идеального упругопластического металла |
Е. МПо 2tof
ино*
1,2 Ю* ■
Механические свойства металла также зависят от температуры. Модули упругости £ и сдвига G снижаются с ро
стом температуры, в то время как коэффициент Пуассона (і несколько возрастает (рис. 6.4). Характер зависимости напряжения о от деформации е при растяжении образца изменяется сложно при повышении температуры. Когда материал рассматривают как идеальный упругопластичс - скнй (рис. 6.5), диаграмма может быть описана лишь двумя
|
бт, МПа
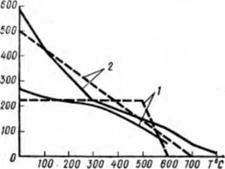
Рис. 6.6. Зависимость предела текучести металлов от температуры: 1 — ииэкоуглероднетая сталь; 2 — татаноаыв сплав |
характеристиками — модулем упругости Е и пределом текучести от : ет=о1/£.
На рис. 6.6 представлены графики зависимости о, от температуры для некоторых металлов (сплошные линии). Иногда эти сложные графики заменяют схематизирован* ными (пунктирные линии). Для низкоуглеродистой стали предел текучести при изменении температуры от 0. . .500 °С принимают постоянным, а затем понижающимся до 0 при 7=600 ’С. В действительности и при 7>600 °С предел текучести металла не равен нулю. Для титанового сплава изменение от принимают в виде одной прямой линии.
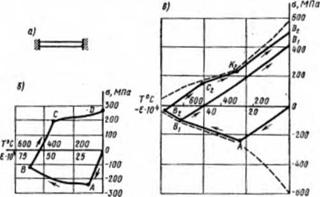
Образование напряжений и деформаций при нагреве и остывании. Изучение собственных напряжений при сварке целесообразно начинать с простейших примеров. Рассмотрим изменение напряжения при нагреве стержня, закрепленного по концам (рис. 6.7, а), до 500 °С и последующем его охлаждении. Будем полагать, что модуль упругости Е и предел текучести о, для ннзкоуглеродистой стали изменяются непрерывно с повышением температуры (см. рис. 6.4 и 6.6). Материал идеальный упругопластическнй (см. рис. 6.5). Напряжения сжатия на рис. 6.6, б будем откладывать вниз, а напряжения растяжения — вверх; полные деформации удлинения, равные сумме упругих и пластических,— вправо, а деформации укорочения — влево. Для определения деформаций будем использовать формулу
(6.2) , а для определения напряжений — формулу
о = £еупр. (6.7)
В закрепленном по концам стержне наблюдаемая деформация еи равна нулю. Поэтому из (6.2) для полной собственной де<{юрмацни
е = £тлр+ (6-8)
Так как при нагреве еа>0, то согласно (6.8) е^^р-Ь
+еал<0. Поэтому кривая из точки 0 идет вниз влево.
|
Рис. 6.7. Образование напряжений в стержне с жестко заделанными концами: а — схема испытания, б — напряжения и деформация на стержне иа низксугле - родистой стали: »— напряжения н деформации и стержне н> гитанового сплава |
В расчетах используется действительная зависимость от от температуры, показанная сплошной линией 1 (см. рис. 6.6), изменение модуля упругости Е происходит, как показано на рис. 6.4, коэффициент линейного расширения а принимаем не зависящим от температуры в диапазоне 0.. .600 °С и равным 12- Ю'*’С~1;отсчеттемператур ведется от О °С. Пока напряжение а не достигнет предела текучести в некоторой точке А, соответствующей температуре примерно 100 °С, пластических деформаций нет. Участок ОА не является прямой линией потому, что по мере повышения температуры модуль упругости Е несколько уменьшается и согласно (6.7) напряжения не зависят линейно от еупр.
В точке А напряжения достигают предела текучести. При дальнейшем повышении температуры напряжение ат, хотя полная деформация е=—еа, возрастает. На участке АВ вследствие падения от напряжение снижается. В точке В нагрев стержня прекращается. В стержне имеются пластические деформации еплВ, равные, согласно (6.8),
рплЯ = “ еаЯ~ •'упрв* (в-9)
где еуирВ=— о, я/£в; оГд и Ев — предел текучести и модуль упругости металла при температуре Тв.
При охлаждении отсчет пластических деформаций еил на стадии остывания стержня следует начать заново. Пластические деформации еалВ в формуле (6.4) будут играть роль начальных деформаций e0(]j|. Так как наблюдаемая деформация равна нулю, имеем
Vp + Afna® —е, пд = е. (6.10)
На участке ВС напряжения нзменятзнак и, пока полная деформация е<от/£, пластические деформации отсутствуют, т. е. Деил=0. В точке С появляются пластические деформации и далее вплоть до полного охлаждения (точка D) напряжения остаются равными пределу текучести металла при соответствующей температуре согласно кривой / (см. рис. .6.6). После полного остывания еа=0. Остаточная пластическая деформация равна алгебраической сумме пластической деформации, возникшей при нагреве, и приращения пластической деіформации, возникшей при остывании. Согласно формуле (6.9), с учетом еа—0, получим
к»п4 "t" ^Спло= еу°Ро= a*ol^D' (6-11)
Остаточная пластическая деформация отрицательна (деформация укорочения). Действительно, если конец растянутого стержня освободить от закрепления, то стержень сократится по длине на размер o, D/£D. В случае жестко заделанного стержня упругая деформация совпадает по абсолютному значению с пластической деформацией. В случае нежесткой заделкн упругая и пластическая деформации обычно не равны друг другу.
Следует обратить внимание на то, что в случае жестко заделанного по концам стержня, согласно формуле (6.8), по горизонтальной оси на рис. 6.7, б откладывается температурная деформация га=аТ. Если считать значение а в некотором интервале температур постоянным, го горнзон-
Т&льную ось можно рассматривать в некотором масштабе и как ось температур.
Рассмотрим аналогичный процесс нагрева стержня из титанового сплава, изменение предела текучести которого показано на рис. 6.6 и в виде пунктирной линии на рис. 6.7, в. Для титанового сплава проведем построения, аналогичные проведенным для стали (см. рис. 6.7, б). Закономерность снижения модуля упругости £ с температурой у титанового сплава примерно такая же, как у низко - углеродистой стали, но значение его у титанового сплава в два раза меньше. Коэффициент линейного расширения, согласно табл. 6.1, примем 8,5[2]10"* °С-1. Напряжения при нагреве достигают предела текучести в точке А при температуре около 300 °С. На участке АВі будут протекать пластические деформации *. Если процесс нагрева прерывать при температуре около 600 С и далее стержень охладить, то напряжения на всем участке BxDt нигде не станут равными пределу текучести. Если нагрев завершить при Т«700 °С в точке Ви то при охлаждении в точке С» возникают пластические деформации, которые, однако, прекращаются в точке К и так как приращение температурной деформации Деа будет меньше приращения Дет=Дох/£, т. е. dtjdT<dir/dT. В этом случае напряжения в стержне хотя и растут, следуя линии K%Dt, но остаются ниже предела текучести металла, в том числе и после полного остывания в точке Dt.
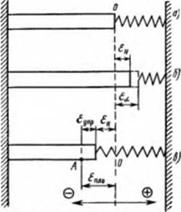
В рассмотренных выше случаях стержень был помещен между двумя абсолютно жесткими стенками (рис. 6.7, а) и поэтому наблюдаемая деформация ен была равна нулю. В свариваемых пластинах волокна металла не находятся в условиях жесткой заделки, так как соседние участки металла могут деформироваться. Реальному поведению металла в свариваемых деталях лучше соответствует модель стержня, конец которого прикреплен к пружине, заделанной в жесткую опору. На рис. 6.8, а пружина не напряжена. Если стержень нагреть (рис. 6.8, б), то он удлинится, но наблюдаемая деформация е„ окажется меньше температурной деформации еа, так как пружина оказывает сопротивление свободному расширению стержня. Собственная деформация, равная разности наблюдаемой и температурной е„—еа, будет отрицательной, что указывает на наличие в стержне сжимающих напряжений. Если эти сжимающие
напряжения достигнут предела текучести, то в стержне будет протекать пластическая деформация осадки. После полного остывания (рис. 6.8, в) стержень окажется короче,
|
Рис. 6.8. Деформация стержня, скреплеиного с пружиной |
чем он был вначале. Однако пружина не даст стержню занять положение, обозначенное точкой А. По отношению к начальному положению в стержне будут: пластическая деформация укорочения еил, возникшая при нагреве и имеющая отрицательный знак; наблюдаемая отрицательная деформация е„; положительная (по отношению к точке Л) упругая деформация eynt), которая вызовет в стержне остаточные напряжения растяжения
о Ее удр.
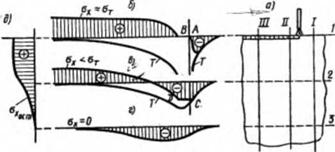
Выше были рассмотрены примеры определения на пряжений в стержнях, жестко закрепленных по концам. В некоторых простейших случаях напряжения при сварке могут быть определены точно таким же способом. Например, с использованием гипотезы плоских сечений могут быть просто определены напряжения в очень широкой пластине, по кромке которой перемещается источник нагрева (рис. 6.9, а). Поперечные сечения /, II, III принимаем не искривляющимися и не перемещающимися относительно друг друга. Рассматриваем только напряжения ох - В продольных сечениях I, 2 и 3 будут разные термические циклы, показанные на рис. 6.9, б. . .г. Временные напряжения ох будут зависеть от температуры и характера ее изменения. На рис. 6.9, б в области высоких температур, когда предел текучести близок к нулю, напряжения на участке АВ отсутствуют, далее появляются растягивающие напряжения, которые достигают предела текучести. На рнс. 6.9, в напряжения сжатия в сечении 2 на участке CD равны пределу текучести, затем меняют знак, но в процессе остывания металла не достигают предела текучести. В сечении 3 максимальные температуры незначительны, напряжения сжатия не вызывают пластической деформации (рис. 6.9, г), и после полного остывания напряжения ох в
этой точке отсутствуют. Эпюра остаточных напряжений сх в поперечном сечении показана на рис. 6.9, д.
Расчетное определение собственных напряжений. Более сложным является определение сварочных напряжений в случае, когда искривлением сечений можно пренебречь, но взаимные перемещения поперечных сечений в процессе сварки относительно друг друга необходимо учитывать.
|
Рис. 6.9. Образование временных и остаточных напряжений при нагреве кромки широкой пластины движущимся источником теп- лоты |
Для определения сварочных напряжений в сталях в этих случаях могут быть использованы простейшие графорасчетные методы Г. А. Николаева и Н. О. Окерблома. В этих методах приняты следующие допущения.
1. Рассматривают только продольные напряжения <тх. Поперечные напряжения оу и касательные тх„ считают равными нулю.
2. Поперечные сечения плоские, но могут перемещаться относительно друг друга.
3. Зависимость предела текучести для низкоуглеродистой стали схематизирована по типу, показанному пунктирной линией / (см. рис. 6.6).
4. Материал идеальный упругопластическнй (см. рис. 6.5).
5. Модуль упругости Е постоянен во всем диапазоне температур.
6. Свариваемые пластины, каждая шириной В, считают достаточно длинными (рис. 6.10,6), чтобы можно было использовать квазнстационарное распределение температур; температура по толщине пластин распределена равномерно.
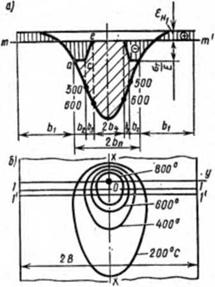
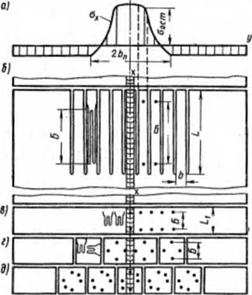
На рис. 6.10, 6 показано квазистационарное распределение температур при сварке длинных в направлении х—х пластин. В методе Г. А. Николаева рассматриваются деформации и напряжения только в двух сечениях пластины; в сечении /—1, соответствующем наибольшей ширине изотермы 600 °С, и в сечении 2—2 после полного остывания пластины (сечение 2—2 на рисунке не показано). Считается, что свариваемые встык пластины собраны на прихватках и относительно друг друга не поворачиваются, т. е. это соответствует случаю укладки шва на целую пластину шириной 2В.
|
|
|
Рис. 6.10. Определение одноосных сварочных напряжений графорасчет - иыы методом Г. А. Николаева: а — эпюра продольных деформаций и сечении /—/; 6 — поле температур при саарце: а — эпюра продольных деформаций, возникших на стадии остывания |
|
|
Рассмотрим распределение собственных напряжений и деформаций в сечении /—/, исполь зуя равенство (6.4). Перед сваркой начальные де(}юрмацни е„пд были равны нулю, а температурные в рассматриваемом сечении га=аТ. Тогда, перенося в левую часть еупр+еил, а в правую часть е„ и меняя знак, получаем
етпи, + ^еіи, —pi, 8а, —
= е„-а7 (6.12)
Решим уравнение (6.12) графически. Возьмем рядом с сечением /—/ второе сечение /'—/', находящееся от него на расстоянии, равном единице. Температурная деформация выделенной полоски в направлении Ох составит а Т. Отложим значения величины —аТ, находящейся в правой
части уравнения (6.12), в виде толстой кривой линии вниз как отрицательные (см. рис. 6.10, а). Теперь необходимо определить е„ . Согласно допущению 2, поперечные сечения не искривляются, поэтому наблюдаемая деформация ея полоски между /—/ и /'—/' будет одной и той же по всей ширине пластины 2В. Положение линии т—т', определяющей на рис. 6.10, а значение eMi, можно находить путем подбора методом последовательных приближений, исходя из условия взаимной уравновешенности собственных напряжений в пределах поперечного сечения 1—1. Как известно, собственные напряжения при одноосном напряженном состоянии пропорциональны упругим деформациям о=еупр£. Поэтому достаточно получить уравновешенную эпюру упругих деформаций еупр, чтобы иметь уравновешенность собственных напряжений. Рассмотрим подробно определение упругих и пластических деформаций при произвольно выбранном еН(. После того как проведена линия т—т', показывающая предположительное значение енЬ вниз от т—т' откладывают предельно возможную упругую деформацию еупр=ет—от/£ и проводят горизонтальную линию ас (eT=const) до 7=500 С (см. рис. 6.6). В диапазоне 500. . .600 °С предел текучести меняется линейно, поэтому на участке се упругая деформация убывает до нуля и остается нулевой при 7>600 С.
На рис. 6.10, а вертикально заштрихована эпюра упругих де<}юрмаций; косо — эпюра пластических деформаций.
Если окажется, что эпюра упругих деформаций уравнове - в
шена, т. е. ^ Вул,, di/ = 0, то гПі выбрана удачно. Если - в
нет, то нужно задаваться новым положением линии т—т' и повторить построение.
Наблюдаемая деформация еНі на рис. 6.10, а оказалась положительной и это означает,’ что пластина в процессе нагрева при сварке удлиняется. Упругие деформации удлинения показаны со знаком плюс, а деформации укорочения — со знаком минус. Зоны шириной Ьг испытывают только упругие деформации, зоны Ьг и 6, — упругие и пластические, а зона Ь, — только пластические деформации. Зоны Ьг, bа и b, составляют так называемую зону пластических деформаций 2Ьа.
Для определения остаточных деформаций и напряжений нужно рассмотреть стадию остывания пластины, т. е. перейти от распределения деформации в сечении /—/ к распределению деформаций в некотором сечении 2—2, условно находящемся при температуре, равной О °С. Для этого следует воспользоваться уравнением (6.4), в котором в качестве начальных деформаций будут присутствовать пластические деформации, найденные в сечении 1—I. По отношению к состоянию в сечении 2—2 состояние в сечении 1—/ является начальным.
Перепишем уравнение (6.4) в другом виде, введя индексы для рассматриваемого состояния:
Єтпр.+ ДЄпд.^Є,, —ва, —e„nli. (6.13)
Так как после полного остывания Т=О °С, то еа,=0.
Для определения упругих и пластических деформаций Аепл, воспользуемся графическим методом. Отложим на рис. 6.10, в в виде толстой линии эпюру —ЄопЛі. Начальные деформации е»„Лі=ДеМі в сечении 1—1. Так как пластические деформации Де,^ были деформациями укорочения волокон металла при нагреве и имеют знак минус, то — el>(U>=»—AeMi будет положительной, поэтому она отложена вверх. Искомая деформация евш будет одинакова по всей ширине пластины, так как принята гипотеза плоских сечений. Далее необходимо задаться некоторой отрицательной величиной ея>, сдвинув начало координат на линию п—п'. Ординаты кривой kfpj'k' выражают левую часть равенства (6.13), т. е. сумму упругих и приращений пластических деформаций, соответствующих стадии остывания. Чтобы получить отдельно значения упругой и пластической составляющих, необходимо воспользоваться пределом текучести от при комнатной температуре и определить максимально возможную упругую деформацию eynpimJX=eT. Отложим ет=от/£ на рис. 6.10, в. Тогда косо заштрихованная часть fpf будет выражать приращения пластических деформаций удлинения Aenjtj; возникших при остывании, а вертикально заштрихованная часть
эпюры — упругие деформации. Если окажется, что в
[ ey„p, df/ = 0, то положение линии п—п' выбрано удачно. - в
Если эпюра упругих деформаций, пропорциональных остаточным напряжениям, не уравновешена, то следует задаться новым положением п—л', т. е. новым eHi. Остаточные пластические деформации е11Л ост равны алгебраической сумме пластических деформаций при нагреве ДепЛ) и приращений пластических деформаций при остывании Агпя (эпюра aft'a'):
*ТМ. ОСТ ~ А£ПД, - f (6.14)
Так как в рассматриваемом случае Лелл по модулю больше AenJs, то знак епл вст совпадает' со знаком Аеул. Эю означает, что остаточные пластические деформации представляют собой деформации укорочения.
Метод Г. А. Николаева позволяет получить распределение остаточных напряжении оОСг=еупр>^ и относительное укорочение сваренной пластины ен.’ Как следует из расчета, максимальные остаточные напряжения в низкоуг - лсроднстой стали являются растягивающими, равны пределу текучести и наблюдаются в зоне шва и зоне термического влияния нагревающейся до сравнительно высоких температур. В основном металле, где температура была ниже (200. . .300 °С), остаточные напряжения — сжимающие.
В методе Н. О. Окерблома определение деформаций и напряжений производится в нескольких последовательно расположенных друг за другом сечениях, что позволяет проследить изменение упругих и пластических деформаций в процессе сварки. В первом сечении начальные деформации принимаются равными нулю. В последующих сечениях в качестве начальных деформаций е0(и присутствуют пластические деформации, полученные для предыдущего сечения. Уравнение (6.12) преобразуется к следующему виду для л-го сечения:
eyn|'n "Ь АЄпля = - в»плп» (6 15)
где начальная деформация е0 „лл может быть представлена как пластическая деформация, накопленная на предыдущих этапах:
п-1
Є. плп = Єплв.,= 2 (6.16)
Переходя от сечения к сечению, можно получить в каждом из них распределение упругих деформаций и напряжений, а также наблюдаемые деформации.
Алгоритм графорасчетных методов относительно несложен. При наличии соответствующей программы расчет напряжений может быть выполнен достаточно быстро на ЭВМ.
При необходимости можно учесть зависимость модуля упругости Е от температуры, а также структурные превращения. В последнем случае температурные деформации га берутся непосредственно с днлатограммы ((at. рис. 6.2, б) при соответствующих температурах.
Точное определение напряжений и деформаций при сварке проводят методами теории пластичности 13), как правило, с использованием метода конечных элементов на мощных ЭВМ. Все тело рассматриваемой пластины разбивают на конечные элементы, более мелкие в зоне нагрева и более крупные в малонагретых частях пластины. Процесс сварки разбивают на небольшие отрезки времени. Сначала напряжения и деформации вычисляют в конце первого отрезка времени Д7» и находят поле упругих и пластических деформаций. Затем, зная поле пластических деформаций в конце Д/і и приращение температурных деформаций на отрезке времени Д/*, определяют упругие и пластические деформации в конце отрезка времени Дtt. Решение продолжают до получения установившегося характера напряжений и деформаций при сварке пластины. В этом методе могут быть учтены любые изменения свойств металла, вызванные изменением температуры и пластической деформацией. Метод позволяет получить напряжения ах, тхр и все компоненты деформации в элементах пластины.
Аналитические методы решения ввиду сложности сварочных задач большого распространения не получили.
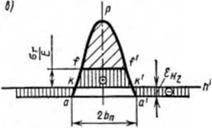
Экспериментальные методы измерения сварочных напряжений. Существуют экспериментальные методы определения остаточных напряжений: рентгеновский, магнитный, ультразвуковой и механические. Чаще используют механические методы, которые основаны на измерении деформаций металла при освобождении его от остаточных напряжений. В качестве измерительных преобразователей перемещений часто используют механические приборы и тензорезисторы, значительно реже — индуктивные и пневматические преобразователи. Рассмотрим пример определения одноосных остаточных напряжений ах в сварной пластине (рис. 6.11, а). До разрезки пластины на полосы (рис. 6.11, б) на ней делают специальные отверстия на расстоянии Б для установки на них механических измерительных приборов или наклеивают тензорезисторы. Размер баз Б несуществен (обычно 10. . .100 мм), так как предполагают, что напряжения в этом случае достаточно мало изменяются по длине. Чтобы учесть возможный изгиб, снимают показания приборов с двух сторон пластины. Затем пластину режут на паюсы шириной Ь. Проводят последующие измерения, и по разности показаний приборов определяют деформацию е, и остаточные напряжения:
Можно вырезать поперечную полоску размером Lt (рис. 6.11, в), который не должен быть более Ьа, т. е. ПОЛОвины ширины зоны пластических деформаций 2Ьа. При этом одноосные напряжения также снимаются достаточно полно.
Для определения двухосных напряжений базы Б квадратики при разрезке нужно брать по возможности меньших размеров (рис. 6.11, г) и в общем случае иметь в каждом квадратике не по две, а по три базы (рис. 6.11,5) для определения ах, о „ и тх„. Если есть уверенность, что
|
Рис. 6.11. Расположение мерительных бази теизодатчнков при определении остаточных сварочных напряжений: а —одноосные напряжении сг^в пластине: б — разрезке на полосы; а — вырезка поперечной полосы; г — разрезка на квадраты с измерением в двух направлениях; д — разрезка на квадраты с намерением в трех направлениях вблизи шва |
касательные напряжения тЛ„ малы, то, чтобы вычислить остаточные напряжения, достаточно измерить возникающие в результате разрезки деформации ех и ev по двум главным направлениям:
°жоег - — £(** + *и)/( 1 — и*);
О, ест + (6.18)
Двухосные остаточные напряжения на поверхности массивных тел определяют аналогично описанному выше для пластины. Металл вокруг измеренных баз подрезают кольцевым сверлом или фрезами на глубину, которая составляет не менее 0,6 размера стороны квадрата или диаметра.
Для определения остаточных напряжений в глубине металла сверлят тонкие глубокие отверстия и размещают в них измерительные преобразователи в различных направлениях. Производят начальные измерения, а затем нз металла вырезают цилиндры диаметром не менее пяти диаметров отверстий, причем отверстие находится в центре цилиндра. На таком расстоянии напряжения не искажены сверлением отверстия. Повторные измерения позволяют определить необходимые для подсчета трехосных напряжений деформации.
Временные напряжения в процессе сварки определяют, устанавливая на поверхность детали три близко расположенных деформометра, которые непрерывно регистрируют наблюдаемые деформации е*„, е„н и у*ун - Зачеканеннон в деталь вблизи баз термопарой непрерывно измеряют температуру, затем на дилатометре определяют дилатограмму металла при заданном термическом цикле сварки. Из дила - тограммы получают закон изменения температурной деформации еа во времени, а по разностям е,„—еа и е„„— —еа находят закон изменения собственных деформаций. Разбивая весь процесс на отдельные отрезки времени At и получая приращения собственных деформаций Ае„ Де„ и Аух„ на каждом из этих отрезков, методами теории пластичности вычисляют временные напряжения (31.