СОЕДИНЕНИЕ МЕТАЛЛОВ В ТВЕРДОЙ ФАЗЕ

МОДЕЛЬ АКТИВАЦИИ КОНТАКТНЫХ ПОВЕРХНОСТЕЙ

Главные особенности активации контактных поверхностей при соединении металлов в твердой фазе обусловлены тем, что каждая из фаз представляет систему, в которой образующие ее атомы свя­заны между собой межатомными силами [94].

Образование межатомных связей (схватывание), как показано Ю. Л. Красулиным [33], происходит на активных центрах. При соединении материалов с реальными поверхностями (атомная и геометрическая неоднородность, наличие окисных и хемосорбиро - ванных слоев) такими центрами являются участки поля упругих искажений вокруг вышедших в зону физического контакта от­дельных дислокаций или их скоплений, в пределах которых энер­гетическое состояние атомов соответствует уровню, необходимому для разрыва старых и образования новых химических связей.

Поэтому кинетика активации контактных поверхностей, обус­ловливающая кинетику развития схватывания, должна находиться в строгом соответствии с закономерностями развития пластической деформации материалов в приконтактной зоне.

При анализе влияния параметров процесса (температуры, дав­ления, времени) на процесс активации контактных поверхностей можно пользоваться представлениями (и уравнениями) химической кинетики, основные положения которой, однако, разработаны для случая взаимодействия газообразных или жидких фаз. Но при этом необходимо учитывать вклад всех энергетических стимуляций процесса, так как среднемассовая температура в виду того, что химическое взаимодействие происходит на активных центрах, не отражает частоту появления активных центров, коллективность взаимодействия и энергетического состояния атомов, участвую­щих в химическом взаимодействии.

Необходимо также иметь в виду, что любая энергетическая стимуляция процесса, с одной стороны, повышает средний энер­гетический уровень, по отношению к которому рассматривается высота потенциального барьера, при достижении или превышении которого осуществляется элементарный акт, а с другой, та же сти­муляция является активирующим фактором и ее необходимо учи­тывать в уравнении, описывающем процесс взаимодействия.

Ввиду важности такого параметра процесса, как температура, проанализируем подробнее ее влияние на кинетику активации контактных поверхностей. Для этого рассмотрим две кинетические кривые роста прочности (отражающие в первом приближении ки­нетику активации контактных поверхностей, т. е. кинетику схва­тывания), полученные при постоянном давлении сварки и различ­ных температурах: Тг и Т2 = Тх - f АТ АТ >0. Повышение

температуры процесса на величин) Т приведет к следующему:

1) увеличится частота выхода дислокаций в зону физического кон­такта; 2) увеличится скорость движения дислокаций и, таким об­разом, увеличится величина энергии, выносимой в зону физиче­ского контакта каждой дислокацией; 3) уменьшится модуль сдвига материала и, таким образом, уменьшится величина энергии, вы­носимой в зону физического контакта каждой дислокацией;

4) уменьшится прочность связей между атомами кислорода и ме­талла в окисном или хемосорбированном слое, и, таким образом, уменьшится высота потенциального энергетического барьера, при достижении или превышении которого осуществится элементар­ный акт (образование химических связей); 5) по причинам, ука­занным в пп. 2—4, изменится число атомов, участвовавших в хи­мическом взаимодействии на одном активном центре (изменится площадь активного центра).

Анализ пп. 1—5 приводит к выводу о том, что следует различать две энергетические характеристики процесса активации контакт­ных поверхностей в условиях термодеформационного воздействия на материалы 194 J:

1. Энергию активации £д в макроскопическом масштабе, обус­ловливающую частоту К появления активных центров в зоне фи­зического контакта; поскольку активным центром является дисло­кация с полем упругих искажений, постольку £д должна пред­ставлять собой энергию активации пластической деформации.

2. Энергетический барьер U, при достижении или превышении которого в пределах отдельного активного центра осуществляется разрыв старых связей, зависящий от физико-химического состоя­ния поверхности.

Очевидно, что при построении модели активации контактных поверхностей необходимо учитывать:

1. Величину энергии, выносимой каждой дислокацией в зону физического контакта с учетом энергии от ее движения.

2. Распределение энергии вокруг дислокации при выходе ее на поверхность с учетом сил зеркального изображения.

3. Частоту выхода дислокаций (появления активных центров) в зону физического контакта при конкретных температурно-ско­ростных условиях сопротивляемости пластическому деформиро­ванию.

4. Величину энергетического барьера, при достижении или превышении которого в пределах отдельного активного центра осуществляется разрыв старых связей.

При построении модели активации контактных поверхностей примем следующие допущения физического (Ф) и математиче­ского (М) характера 195]:

Ф1. Атомы соединяемых поверхностей твердых тел находятся в состоянии физического контакта.

Ф2. Скорость обменных процессов электронного взаимодей­ствия между возбужденными атомами не учитывается, так как она на много порядков выше скорости активации атомов на кон­тактных поверхностях, определяемой частотой выхода дислокаций в зону физического контакта и их энергией.

ФЗ. Параметры сварки (температура и давление) таковы, что образование новых фаз, рекристаллизации и т. п. не происходит. Поэтому скорость активации контактных поверхностей определяет скорость развития схватывания (характер заполнения связями всей площади физического контакта).

Ф4. Химическое взаимодействие происходит на активных центрах.

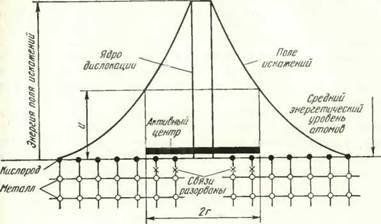
Ф5. Активным центром будем считать область радиуса г вокруг вышедшей на контактную поверхность дислокации, включающую очаг взаимодействия (зону радиусом ~15б 196] вокруг ядра дислокации) и зону релаксации энергии до уровня U.

Ml. Если в результате выхода дислокации в зону физического контакта активируется по крайней мере п атомов в области актив­ного центра на одной из контактных поверхностей, достигая или превышая энергетический барьер U, то они могут образовывать химические связи с атомами другой поверхности. Если такие связи образованы, то они в дальнейшем не разрушаются.

М2. Активные центры считаются независимыми, т. е. вероят­ность возникновения i-того активного центра не зависит от воз­никновения остальных центров.

М3. При постоянных Т и Р процесса каждый выход дислока­ций вызывает активацию постоянного числа п атомов, приводя­щую к достижению U и выше.

М4. Число активных центров, возникающих за конечный про­межуток времени, конечно.

В указанных предположениях введем в рассмотрение случай­ные величины т, — время между появлениями t'-того и і + 1-го центров возмущения. В связи с независимостью активных центров друг от друга (М2) полагаем, что т, есть последовательность не­зависимых и одинаково распределенных с плотностью f (t) слу­чайных величин.

Пусть число активных центров в зоне физического контакта равно С. Тогда сумма т, по всем і от 1 до С, т е. tc — хі + т2 + + т3 + • • *+тс—есть время, в течение которого будет со­здано С активных центров.

Пусть распределение т, имеет среднее р и дисперсию о2. Тогда из центральной предельной теоремы следует, что при С -• оо слу­чайная величина tc имеет асимптотически нормальное распределе­ние со средним (математическим ожиданием) рС и стандартным отклонением о УС. Т. е. для любого фиксированного у

у

limA{/c<pC-f-t/oKC} = y^ J ехр( dU = G(y). (76)

Таким образом, при достаточно большом числе С точное равен­ство (76) можно приближенно выразить

Ptc<yC + yo}^C}^G(y). (77)

В качестве плотности / (t) естественно для такого сорта про­цесса рассматривать экспоненциальный закон распределения, т. е. f (t) = X exp (—Xt), где X— интенсивность (частота) появления активных центров. В этом случае среднее р, = 17., а дисперсия о2 = 1;7,г и формула (77) принимает вид

Р{'с<х +уЩъО(у).(78)

Если вместо случайной величины tc рассматривать нормиро­ванную случайную величину ——то доля (вероятность) такой

О у С

случайной величины, не превосходящей некоторого числа у, т. е.

' oi^g~ < У' равна 6

Практически достоверным в наших условиях можно считать событие, состоящее в том, что

'с<Т + 3-Т <79>

с вероятностью G (3), практически равной 1. При этом у — 3. Поэтому

(«0)

Можно считать, что неравенство (80) выполняется практически всегда.

Решая неравенство (80) относительно С, получим, что Gmin "'С С Сшах,

где

r __ 2Xtc + 9-3V4Ktc -9 .

^mln 9 ’

2Xtc + 9 + 3 УШс+9

Таким образом, почти наверняка неравенство (80) будет вы­полнено для совокупности значений С из интервала (Cmln, Cmax). Однако использование такого интервала для С в дальнейшем неудобно. Поэтому в качестве значения С примем

При выводе соотношения (80) было использовано предполо­жение о показательном характере распределения времени между возникновениями активных центров. Такое предположение яв­ляется достаточно оправданным по следующим причинам, на­блюдающимся (в первом приближении) в реальном процессе:

а) вероятность возникновения активного центра в промежутке времени (t, t + Л/) можно принять равной "К At + 0 (Л/), если At мало;

б) возникновение активного центра в промежутке времени (t, t + АО не зависит от ситуации до момента £;

в) вероятность одновременного возникновения более чем од­ного активного центра пренебрежимо мала (конечно, это допуще­ние является наиболее грубым, однако оно является вполне при­емлемым в силу существования так называемого времени задержки при генерировании дислокаций, которое, по данным Ван Бюрена, для металлов составляет 10 7 с [90]).

В соответствии с конкретными условиями процесса и сделан­ными допущениями рассмотрим более детально величины С и Я, входящие в неравенство (80).

Единственным критерием степени полноты процесса активации контактных поверхностей может быть прочность соединения, выра­жающая степень схватывания. Кинетика роста прочности соеди­нений будет отражать кинетику активации контактных поверх­ностей лишь в том случае, если принятые допущения Ф1, ФЗ и Ml выполняются. Далее в этой главе прочность соединения, выра­жающую степень активации и схватывания контактных поверх­ностей, будем представлять в относительных единицах (представ­ляющих отношение прочности соединения при некоторых пара­метрах Т, Р, t к прочности основного металла, которую можно считать максимально возможной для соединения) и обозначать в зависимости от необходимости через (Тф или через о. При этом всегда будем помнить допущение Ф1.

Естественно, что число активных центров, образованных на соединяемых поверхностях, и величина Оф должны быть опре­деленным образом связаны.

Допустим, что N0 — число атомов на единице площади соеди­няемой поверхности, которые могут участвовать в химическом взаимодействии; —- число атомов, образовавших связь к не­которому моменту времени tp, —- число активных центров, обра­зовавшихся к моменту времени tp, N3 — число атомов, образовав­ших связь к моменту £2; С2 — число активных центров, образо­вавшихся к моменту £2; п — число атомов в каждом активном центре (по предположению М3).

г-, с(/,) — М> с (t2) —

Примем также, что = —— = о. и - гг - = —= о2, _ Л'о <W 1 А0 Сщах 2

Где dj и ог — относительные прочности соединения при тех же

длительностях процессов сварки tt и t2.

Момент времени tx примем за ноль отсчета длительности (t = = t2 — tx) роста относительной прочности аф.

Обозначим число атомов, образовавших связь за время t = = 12 — tu через N, а число активных центров, образовавшихся за это же время, через С, т. е. N = N2 — а С = С2 — С,. Естественно, что N = Сп ив то же время IV — N0 (о2 — о1). Отсюда следует, что

С = - А(.Чг:0i) . (82)

Величина п будет зависеть от энергии возмущения Q, высоты энергетического барьера U и среднего энергетического уровня, по отношению к которому рассматривается высота потенциаль­ного барьера U.

При оценке п в силу условия Ф5 можно воспользоваться урав­нениями, описывающими искажения вокруг дислокации в упру­гом континууме. Энергия искажения k-того ряда атомов вокруг ядра дислокации [90] у поверхности с учетом сил зеркального изображения может быть выражена зависимостью

t'«=-wr(‘-“siT '-)■ t83»

величина смещения &-того ряда равна

як=—|rarctgJ7; (84>

ширина поля дислокации равна

(85>

Q' = 2Q,

где Q — полная энергия дислокации, включающая энергию ядра дислокации и поля искажений вокруг нее; b — модуль вектора Бюргерса;

гк — расстояние в плоскости вектора Бюргерса до рассматри­ваемого &-того ряда; р — коэффициент Пуассона; а — постоянная решетки.

Будем считать (рис. 10), что все атомы на поверхности в поле упругих искажений вокруг дислокации, энергия которых достигла или превысила потенциальный барьер у поверхности U, разры­вают старые (и образуют новые) межатомные связи (Ml; М3). В таком случае для заданного уровня энергии U и соответствую­щих ему радиуса г и смещения R из уравнений (83) и (84) можно записать:

R arccos ( 1 —^Ги) • (86)

соответственно

а, 2tlR (U)

2 (1 — (і) b---- •

Площадь активного центра, учитывая круговую симметрию поля упругих искажений вокруг дислокации, будет

с Г а 2nR(U)Y, йач

s=nr«lg_ь~ • (88)

Число атомов в одном активном центре может быть выражено

как

(89)

Подставляя уравнение (89) в (82) для С, получим

C = ^N() (ст2—а,) (1-М)2 ctg* - Л[и)- ■ (90)

Подставляя далее уравнение (90) в (81), можно определить R (U), а зная R (U), по уравнению (86) можно определить U, а по (87) - г.

Оценим далее величину Q. Из уравнения (86) следует, что об­ласть определения функции arccos х представляет собой отрезок — 1 sS х ^ 1, поэтому

"«тяг - <91>

Таким образом, из формул Ван Бюрена [90] следует лишь оценка энергетического барьера U. Ниже будет показано, при Каких условиях U достигает максимального значения Q/2n2a.

59

По поводу уравнения (86) необходимо также заметить сле­дующее. Это уравнение связывает R — величину смещения атомов, имеющих энергию U, и Q — энергию, равную У] U по всем воз­можным рядам атомов вокруг данной дислокации. Знание R и Q полностью определяет тот барьер U, который может быть преодо­лен рядом атомов, находящихся на расстоянии г [см. уравне­ние (87)], если Q — энергия, выносимая дислокацией в зону соединения.

Известно, что энергия поля искажений вокруг неподвижных винтовой и краевой дислокаций может быть выражена уравне­ниями, учитывающими модуль сдвига, радиус полого цилиндра, для которого оценивается энергия поля искажений, и радиус ядра дислокаций, характеризуемого сильными искажениями, для ко­торого применение линейной теории упругости невозможно [90].

Ван Бюрен [90], Коттрелл [42] и др. предположили, что энергия ядра дислокации, приходящаяся на одну атомную пло­скость, составляет величину, равную 1/10 Gb3, а общая энергия дислокации в любом кристалле по порядку величины составляет Gb3 на одно межатомное расстояние вдоль оси дислокации. Ука­занная оценка справедлива для случая неподвижной дислокации.

Т. А. Конторова, Я. И. Френкель [97] и Эшелби [98] для оценки энергии движущейся дислокации (2ДВ предложили урав­нение, аналогичное уравнению для энергии движущейся массы в теории относительности:

(91)

где Q — энергия неподвижной дислокации; v — скорость движения дислокации; с — скорость звука в кристалле (с 105 см/с).

Из уравнения (92) следует, что при скоростях движения дисло­кации v ^ с/10 энергия движущейся дислокации мало отличается от энергии неподвижной дислокации.

На основе уравнений кинетической теории дислокации можно показать, что для получения скорости движения дислокаций v ^ >=»с/10 скорость пластической деформации в должна составлять величину порядка 104 с1.

При сварке давлением с подогревом даже в период активного деформирования с учетом возможности полного сглаживания ми­кровыступов обработки соединяемых поверхностей за время по­рядка 10 с, значения скоростей деформации составляют величины на несколько порядков ниже указанной (в = 10"3-М0~5 с-1).

Таким образом, при сварке давлением с подогревом, учитывая, что интенсивность пластической деформации соединяемых мате­риалов в зоне контакта (и тем более в объеме) мала, кинетическую энергию движения дислокации ввиду ее малости можно не учи­тывать.

В тех случаях, когда интенсивность пластической деформации велика и скорость движения дислокаций v^c! 10 (сварка взры­вом, магнитно-импульсная сварка), при энергетических оценках процесса необходимо использовать величину энергии движущейся дислокации, определить которую необходимо по уравнению (92).

Сделаем далее оценку величины X, входящей в неравенство (80) и определяемой как частота выхода дислокаций в зоне физиче­ского контакта. Для этого вновь воспользуемся основными по­ложениями кинетической теории дислокаций.

При этом будем предполагать, что для малых скоростей де­формирования, отличающих процесс ползучести, справедлива мо­дель с фиксированными барьерами, которые ограничивают рас­ширение дислокационных петель в кристалле определенным рас­стоянием L0. Ж. Фридель [99] для такой модели показал линей­ную зависимость плотности дислокации от величины дефор­мации є, т. е.

P = T^-e. (93)

Для двух фиксированных значений е0 и 8j (ех = є0 Ж Де на

кривой ползучести) и соответствующих им ро и Pj, предполагая,

что изменение структуры металла в результате деформации на величину Ае не настолько значительно, чтобы существенно из­менить L0, можно записать:

TOC o "1-5" h z ft_p. = 2l! i=!±. (94)

Изменение ПЛОТНОСТИ дислокаций Др = Pj — р0 в единицу вре­мени можно рассматривать в качестве среднего значения частоты выхода дислокаций X в зону соединения, т. е.

і _________ Др 2(et — є0) /qc;

СР~ А/ ~ L06Af ' 1 '

Если в уравнении (95) величину Де = ех — е0 выбирать ра­зумно малой, то значение AelAt будет выражать среднюю ско­

рость ползучести для выбранного (тоже малого) интервала вре­мени At. Из уравнения (95), переходя к пределу при At —> 0, получим

Х = £. (96)

С учетом уравнения (41) можно записать

<97>

где Р равно Рр или близко к нему;

т) = const [см. уравнение (40)].

Анализ этого уравнения приводит к естественному выводу о том, что частота выхода дислокаций в зону соединения определяется интенсивностью пластической деформации соединяемых металлов, а следовательно, ее энергетическими параметрами.

Расчеты, основанные на данных экспериментальных наблюде­ний, показывают, что основной вклад при оценке Cmln и Стах дает

С I Q

член ktc. Кроме того, было принято, что С = - — ■'——. В силу этого с достаточной точностью можно считать, что

С - kic. (98)

Приравнивая правые части уравнений (98) и (90), получаем, что 4 ., л~ /1 у» * о 2лR (U)

Х/с = — iV„ ДОф (1 — р)~ ctg- ,

где ДОф = сг2 — стх.

Ввиду ТОГО ЧТО tc — время роста относительной прочности СГф на величину Доф, то, поделив обе части предыдущего уравнения на tc и устремив tc к нулю, получим

TOC o "1-5" h z х^ -?г <1 ~ и)2 ct§2 Щр ■ (")

Отсюда легко найти R ((/), рассматривая арифметический ко­рень для котангенса. А именно:

R<tO = i arcctg /----------------------------------------- . (100)

Зная R (U), можно далее с помощью формулы (86) получить формулу для Й:

*/ = - Д—„м^фО-Ю*—> (Ш1)

2л° 4Л'0стф (I — ц)2 -лк

где оф — скорость роста прочности при схватывании.

Из полученной формулы следует, что если пк пренебрежимо

мало по сравнению с 4А0аф (1 — р)2, то членом пк можно пре­небречь и формулу (101) заменить приближенной формулой

"=-аЬ - <102>

Итак, полученная формула показывает, что когда частота вы­хода дислокации к пренебрежимо мала по сравнению с Л^сТф, то в оценке (91) V достигает своей верхней границы и лишь когда

к сравнима с А0аф или когда оф мала, для подсчета энергетиче­ского барьера U следует пользоваться формулой (102).

62

Из формул (88) и (100) далее можно найти площадь активного центра: 5 = Но так как Л/Оог 2, то

Отсюда получаем, что

Однако в силу исходного условия Ml формулы (100) и (104) получены только для одной из поверхностей. Поэтому оценим вероятности W одновременного образования пары активных цен­тров, находящихся в поле действия друг друга [100]. В соответ­ствии с уравнением (97) вероятность выхода одного активного

центра Wx = exp, — Ек/!>р ] - Принимая Ек = 30 ккал/моль и

Т = 1000 К, получим U7, = 10'7.

В силу независимости образования активных центров на одной и другой поверхности вероятность образования пар активных цен­тров равна W = WiW2, где V2 — вероятность образования актив­ного центра на второй поверхности. Принимая U7X = W2 (соеди­нение одноименных материалов), получим, что W = (WJ2 10“14.

Так как число всех возможных активных центров на поверх­ности С *=» NJn я» 107, то среднее число пар активных центров, возникших на поверхности при 117 = Ю 14 одновременно, со­ставляет С = 10 14-107 10~7, т. е. практически равно нулю.

Это позволяет считать, что пары активных центров практически не возникают.

Проделанные оценки строились в предположении, что, если на поверхности I образовался t'-тый активный центр, то он яв­ляется источником формирования связей с поверхностью II. В силу предположения Ml заметим, что на время жизни /-того активного центра не накладывается никаких ограничений. В то же время можно сделать оценку вероятности образования пар актив­ных центров, предполагая, что длительность жизни каждого из них конечна. Пусть длительность жизни активного центра равна т, а число всех возможных активных центров на одной поверхности равно С. Тогда, предполагая, что образующиеся активные центры распределены по поверхности равномерно, получим, что вероят­ность образования і-того активного центра будет равна 1/С.

Вероятность образования какого-нибудь одного активного Центра за промежуток времени между t и t + т, т. е. за время т в силу пуассоновского характера их образования равна Кхе Ят. Поэтому вероятность Wr образования фиксированного і'-того центра за время т будет в С раз меньше, т. е. равна Wx = Kx/Cekx.

Предположим теперь, что на поверхности I образовался t'-тый активный центр и что он находится в состоянии, готовом к взаимо­действию с соответствующим активным центром на поверхности II,
если таковой возникает в течение времени т, т. е. за время жизни і-того активного центра на поверхности I. При этом вероят­ность Wx образования j'-того активного центра на поверхности II (для случая соединения одноименных металлов) за промежуток вре­мени т равна

Wx — )л/Сеи.

Оценки, основанные на данных экспериментальных наблюде­ний, показывают, что при т = 10-9-ь10в с значения VX лежат в диапазоне Ю"11—10“7.

Вероятности Wx при этом были подсчитаны в предположении, что на поверхности I номер центра і закреплен. Поскольку за­ранее неизвестно, о какой паре активных центров идет речь, то активный центр на первой поверхности выбирается наугад (с веро­ятностью 1/С). Поэтому найденные вероятности Wx следует раз­делить на 107. Ясно, что полученные в результате такого деления числа пренебрежимо малы.

Заметим, что если продолжительность жизни активного центра т есть случайная величина с некоторым законом распределения, то соответствующие вероятности Wx могут разве лишь уменьшиться.

Итак, и в ранее рассмотренном варианте, и в последнем случае образованием пар активных центров (при любом предположении относительно продолжительности их жизни) можно пренебречь. Выполненный расчет вынуждает считать, что энергии активного центра на одной поверхности оказывается достаточной для акти­вации атомов второй поверхности. Поэтому потоки активных цен­тров, выходящих на каждую из поверхности, накладываются один на другой, и это необходимо учитывать при использовании уравне­ний (80), (101) и (103): вместо К следует брать 21 (при соединении одноименных материалов). При этом уравнение (103) примет вид:

Уравнение (101) с использованием выражения для S преобразуется в

Q 45(1-н)

2п2а 4S (1 — ц) + па2

Ввиду того что понятия «активированного состояния», «акти­вированного комплекса» и другие связанные с ними понятия полу­чили свое определение и наибольшее развитие лишь при изучении химических реакций в жидкой и газовой фазах, представляется целесообразной попытка дать соответствующие определения для различных процессов взаимодействия в кристаллических телах [100]. Точнее, даже не определения вышеуказанных понятий, так как очевидна тщетность таких попыток даже сегодня, а введение

достаточно подходящего математического эквивалентна. Такая попытка может дать определенные результаты по следующим сооб­ражениям.

Из проделанных расчетов и рассуждений следует, что для числа активных центров С имеет смысл использовать формулу (98):

где к — среднее значение переменного параметра к (t) за промежу­ток времени tc.

Очевидно, что такая формула будет справедлива лишь в случае, когда С не является случайной величиной. Однако из физических представлений следует, что С есть случайная величина. При таком подходе модель активации контактных поверхностей, мало изме­няясь в аналитическом плане, становится более корректной в фи­зическом отношении. Кроме того, такой подход позволит про­двинуться в построении математического эквивалента для поня­тий, связанных с термином «активация».

Сохраним условия Ф1—Ф5 и Ml—М3, однако условие М4 за­меним на М4' — число активных центров случайно и эту случай­ную величину обозначим также через С. Снова введем в рассмотре­ние случайные величины т(- (г = 1, 2, 3, 4, 5, . . .) — время между возникновениями последовательности активных центров [100].

Если считать, что первый активный центр возникает в началь­ный момент времени І = 0, ТО В момент времени t = Tj мгновенно возникает второй активный центр. Далее в момент t = -{- т2

возникает третий активный центр. Последовательность |т;| есте­ственно предполагать последовательностью взаимно независимых, неотрицательных и одинаково распределенных случайных величин. Кроме того, будем считать, что т£ = 0 с вероятностью 1.

Простым процессом активации будем называть случайную по­следовательность {т1( т2, т3, . . ., тк. . .}, удовлетворяющую ука­занным условиям.

Если первый активный центр возникает не в момент t — 0, а в некоторый момент, выбранный на положительной полуоси вре­мени в соответствии с заданным заранее распределением вероят­ностей, то процесс активации будет начинаться с другой случай­ной величины т0, также неотрицательной и независимой от {т,[, і = 1,2,..., но не обязательно имеющей то же распределение, что и [т,- [, 1 = 1,2,...

Такую последовательность (т0, xlt т2, . } будем называть

общим процессом активации.

Обозначим через tc = - J - т2 - f. . . - J - тс момент времени,

когда возникает С-тый активный центр. Пусть Ct—наибольшее зна­чение С, для которого tc t, т. е. число активных центров, воз­никших до момента времени t (включая и активный центр, воз­никший в момент /). Обозначим далее А (/) = MCt и назовем эту функцию А (t) — функцией активации. Заметим, что знание

5 Э. С. Каракозов
функции активации или по крайней мере ее асимптотического по­ведения при больших t позволяет ответить на многие интересные вопросы, касающиеся процесса активации.

Грубо говоря, А (t) — это среднее число активных центров, возникших до момента t, если это среднее вычислено по большому количеству реализаций процесса активации.

Относительно функции активации А (t) известна следующая теорема [101 ]: если щ = Мт,- «S оо, то

= (107)

/-»СО ' Й1

Если, как и ранее, считать, что т,- имеют показательное рас­пределение с плотностью I (t) = ке~и, где к — средняя интенсив­

ность появления активных центров за некоторый промежуток t, то р. = 1/А и из формулы (107) следует, что

А (і) = U (108)

при всех t ^ 0 из указанного промежутка (если при соответствую­щих к справедлив закон больших чисел).

Таким образом, формулы (98) и (108) близки по своей структуре, однако смысл этих формул различен. В частности, вместо точного числа активных центров в формулу (108) входит среднее их число. С физической точки зрения кажется, что природе больше отвечает подход с помощью формулы (108).

Если все {т,}, і = 1, 2, . . ., имеют абсолютно непрерывную функцию распределения F (х), то A (t) можно продифференцировать и получить из нее плотность активации a (t) = А' (t). В. Л. Сми­том [102] доказано, что, если lim f (х) = 0, и, если для некото-

Х-Усо

рого Р > 1 величина | / (х) |р интегрируема, то

TOC o "1-5" h z lima(0 = -^-, (109)

t >ОЭ Hi

а в случае показательного распределения т,-, і = 1,2,...

а (/) = К (110)

при всех t ^ 0 из указанного выше промежутка т, в котором опре­деляется к.

Таким образом, если плотность распределения т,, /=1,2,... показательна, то для всех t ^ 0 плотность активации и частота (интенсивность) образования активных центров представляет собой одно и то же. В силу того что функция активации A (t) может быть легко восстановлена по плотности активации а (t), то из соотно шений (109) и (110) следует, что в частоте образования активных центров "к по крайней мере для больших t содержится вся инфор­мация относительно процесса активации.

Предельное распределение для числа активных центров Ct, возникающих до момента времени t, является асимптотически нормальным при больших t СО средним І, Щ И дисперсией СҐ//рі [103]. Если поток активных центров пуассоновский, то ц, = 1Д, a Ct тогда распределено асимптотически нормально со средним и дисперсией, равными Kt. Этот результат по существу был ис­пользован при построении модели с фиксированным С.